One application for derivatives is to estimate an unknown value of a function at a point by using a known value of a function at some given point together with its rate of change at the given point. If [latex]f(x)[/latex] is a function defined on an interval [latex][a,a+h][/latex], then the amount of change of [latex]f(x)[/latex] over the interval is the change in the [latex]y[/latex] values of the function over that interval and is given by

The average rate of change of the function [latex]f[/latex] over that same interval is the ratio of the amount of change over that interval to the corresponding change in the [latex]x[/latex] values. It is given by

As we already know, the instantaneous rate of change of [latex]f(x)[/latex] at [latex]a[/latex] is its derivative

For small enough values of [latex]h, \, f^{\prime}(a)\approx \frac{f(a+h)-f(a)}{h}[/latex]. We can then solve for [latex]f(a+h)[/latex] to get the amount of change formula:

We can use this formula if we know only [latex]f(a)[/latex] and [latex]f^{\prime}(a)[/latex] and wish to estimate the value of [latex]f(a+h)[/latex]. For example, we may use the current population of a city and the rate at which it is growing to estimate its population in the near future. As we can see in Figure 1, we are approximating [latex]f(a+h)[/latex] by the [latex]y[/latex] coordinate at [latex]a+h[/latex] on the line tangent to [latex]f(x)[/latex] at [latex]x=a[/latex]. Observe that the accuracy of this estimate depends on the value of [latex]h[/latex] as well as the value of [latex]f^{\prime}(a)[/latex].

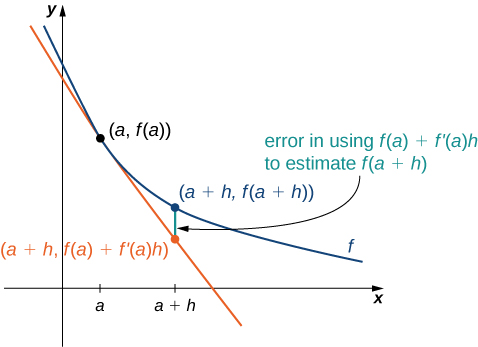
Figure 1. The new value of a changed quantity equals the original value plus the rate of change times the interval of change: [latex]f(a+h)\approx f(a)+f^{\prime}(a)h[/latex].

Watch the following video to see the worked solution to Example: Estimating the Value of a Function.