Combining Functions

Learning Outcomes

  • Make new functions from two or more given functions

Composite Functions

Now that we have reviewed the basic characteristics of functions, we can see what happens to these properties when we combine functions in different ways, using basic mathematical operations to create new functions. For example, if the cost for a company to manufacture [latex]x[/latex] items is described by the function [latex]C(x)[/latex] and the revenue created by the sale of [latex]x[/latex] items is described by the function [latex]R(x)[/latex], then the profit on the manufacture and sale of [latex]x[/latex] items is defined as [latex]P(x)=R(x)-C(x)[/latex]. Using the difference between two functions, we created a new function.

Alternatively, we can create a new function by composing two functions. For example, given the functions [latex]f(x)=x^2[/latex] and [latex]g(x)=3x+1[/latex], the composite function [latex]f\circ g[/latex] is defined such that

[latex](f\circ g)(x)=f(g(x))=(g(x))^2=(3x+1)^2[/latex]

 

The composite function [latex]g\circ f[/latex] is defined such that

[latex](g\circ f)(x)=g(f(x))=3f(x)+1=3x^2+1[/latex]

 

Note that these two new functions are different from each other.

Combining Functions with Mathematical Operators

To combine functions using mathematical operators, we simply write the functions with the operator and simplify. Given two functions [latex]f[/latex] and [latex]g,[/latex] we can define four new functions:

[latex]\begin{array}{cccc}(f+g)(x)=f(x)+g(x)\hfill & & & \text{Sum}\hfill \\ (f-g)(x)=f(x)-g(x)\hfill & & & \text{Difference}\hfill \\ (f·g)(x)=f(x)g(x)\hfill & & & \text{Product}\hfill \\ \Big(\frac{f}{g}\Big)(x)=\frac{f(x)}{g(x)} \, \text{for} \, g(x)\ne 0\hfill & & & \text{Quotient}\hfill \end{array}[/latex]
Often these functions have more than one term, so when you perform operations on them you will need to remember how to work with polynomials.

Recall: Given multiple polynomials, add or subtract them to simplify the expressions

  1. Combine like terms.
  2. Simplify and write in standard form. Standard form means you start with the leading term, and write the rest of the terms in descending order by degree.

BE CAREFUL WHEN SUBTRACTING POLYNOMIALS!

When subtracting a polynomial from another, be careful to subtract each term in the second from the first. That is, use the distributive property to distribute the minus sign through the second polynomial.

[latex]\begin{array}{cc}\left(3x^2-2x+9\right)-\left(x^2-4x+5\right)\text{}\hfill &\text{Distribute the negative in front of the parenthesis} \hfill \\ 3x^2-2x+9 -x^2 -\left(-4x\right) - 5\hfill & \text{Be careful when subtracting a negative}.\hfill \\ 3x^2 - x^2 -2x+4x+9-5\hfill & \text{Rearrange terms in descending order of degree} \hfill \\ 2x^2 +2x +4 \hfill & \text{Combine like terms}. \hfill \end{array}[/latex]

Recall: Given two binomials, Multiplying Using FOIL

  1. Multiply the first terms of each binomial.
  2. Multiply the outer terms of the binomials.
  3. Multiply the inner terms of the binomials.
  4. Multiply the last terms of each binomial.
  5. Add the products.
  6. Combine like terms and simplify.Two quantities in parentheses are being multiplied, the first being: a times x plus b and the second being: c times x plus d. This expression equals ac times x squared plus ad times x plus bc times x plus bd. The terms ax and cx are labeled: First Terms. The terms ax and d are labeled: Outer Terms. The terms b and cx are labeled: Inner Terms. The terms b and d are labeled: Last Terms.

Example: Combining Functions Using Mathematical Operations

Given the functions [latex]f(x)=2x-3[/latex] and [latex]g(x)=x^2-1[/latex], find each of the following functions and state its domain.

  1. [latex](f+g)(x)[/latex]
  2. [latex](f-g)(x)[/latex]
  3. [latex](f·g)(x)[/latex]
  4. [latex]\Big(\frac{f}{g}\Big)(x)[/latex]

Watch the following video to see the worked solution to Example: Combining Functions Using Mathematical Operations

 

You can think of the domain of a function as all possible inputs that will produce a valid output. When you think about it this way, you will see that fractional functions that have a variable in the denominator (when a denominator is zero, you have an undefined value) or a variable under an even root radical (you cannot evaluate a negative value under an even square root), you will have restrictions in your domain.

Recall: Given a function written in an equation form that includes a fraction, find the domain.

  1. Identify the input values.
  2. Identify any restrictions on the input. If there is a denominator in the function’s formula, set the denominator equal to zero and solve for [latex]x[/latex] . These are the values that cannot be inputs in the function.
  3. Write the domain in interval form, making sure to exclude any restricted values from the domain.

Find the domain of the function [latex]f\left(x\right)=\dfrac{x+1}{2-x}[/latex].

Recall: Given a function written in equation form including an even root, find the domain.

  1. Identify the input values.
  2. Since there is an even root, exclude any real numbers that result in a negative number in the radicand. Set the radicand greater than or equal to zero and solve for [latex]x[/latex].
  3. The solution(s) are the domain of the function. If possible, write the answer in interval form.

Find the domain of the function [latex]f\left(x\right)=\sqrt{7-x}[/latex].

Try It

For [latex]f(x)=x^2+3[/latex] and [latex]g(x)=2x-5[/latex], find [latex]\left(\frac{f}{g}\right)(x)[/latex] and state its domain.

 

 

Function Composition

When we compose functions, we take a function of a function. For example, suppose the temperature [latex]T[/latex] on a given day is described as a function of time [latex]t[/latex] (measured in hours after midnight) as in Figure 6. Suppose the cost [latex]C[/latex], to heat or cool a building for 1 hour, can be described as a function of the temperature [latex]T[/latex]. Combining these two functions, we can describe the cost of heating or cooling a building as a function of time by evaluating [latex]C(T(t))[/latex]. We have defined a new function, denoted [latex]C\circ T[/latex], which is defined such that [latex](C\circ T)(t)=C(T(t))[/latex] for all [latex]t[/latex] in the domain of [latex]T[/latex]. This new function is called a composite function. We note that since cost is a function of temperature and temperature is a function of time, it makes sense to define this new function [latex](C\circ T)(t)[/latex]. It does not make sense to consider [latex](T\circ C)(t)[/latex], because temperature is not a function of cost.

Definition

Consider the function [latex]f[/latex] with domain [latex]A[/latex] and range [latex]B[/latex], and the function [latex]g[/latex] with domain [latex]D[/latex] and range [latex]E[/latex]. If [latex]B[/latex] is a subset of [latex]D[/latex], then the composite function [latex](g\circ f)(x)[/latex] is the function with domain [latex]A[/latex] such that

[latex](g\circ f)(x)=g(f(x))[/latex]

A composite function [latex]g\circ f[/latex] can be viewed in two steps. First, the function [latex]f[/latex] maps each input [latex]x[/latex] in the domain of [latex]f[/latex] to its output [latex]f(x)[/latex] in the range of [latex]f[/latex]. Second, since the range of [latex]f[/latex] is a subset of the domain of [latex]g[/latex], the output [latex]f(x)[/latex] is an element in the domain of [latex]g[/latex], and therefore it is mapped to an output [latex]g(f(x))[/latex] in the range of [latex]g[/latex]. In Figure 12, we see a visual image of a composite function.

An image with three items. The first item is a blue bubble that has two labels: “domain of f” and “domain of g of f”. This item contains the numbers 1, 2, and 3. The second item is two bubbles: an orange bubble labeled “domain of g” and a blue bubble that is completely contained within the orange bubble and is labeled “range of f”. The blue bubble contains the numbers 0 and 1, which are thus also contained within the larger orange bubble. The orange bubble contains two numbers not contained within the smaller blue bubble, which are 2 and 3. The third item is two bubbles: an orange bubble labeled “range of g” and a blue bubble that is completely contained within the orange bubble and is labeled “range of g of f”. The blue bubble contains the numbers 4 and 5, which are thus also contained within the larger orange bubble. The orange bubble contains one number not contained within the smaller blue bubble, which is the number 3. The first item points has a blue arrow with the label “f” that points to the blue bubble in the second item. The orange bubble in the second item has an orange arrow labeled “g” that points the orange bubble in the third item. The first item has a blue arrow labeled “g of f” which points to the blue bubble in the third item. There are three blue arrows pointing from numbers in the first item to the numbers contained in the blue bubble of the second item. The first blue arrow points from the 1 to the 0, the second blue arrow points from the 2 to the 1, and the third blue arrow points from the 3 to the 0. There are 4 orange arrows pointing from the numbers contained in the orange bubble in the second item, including those also contained in the blue bubble of the second item, to the numbers contained in the orange bubble of the third item, including the numbers in the blue bubble of the third item. The first orange arrow points from 2 to 3, the second orange arrow points from 3 to 5, the third orange arrow points from 0 to 4, and the fourth orange arrow points from 1 to 5.

Figure 12. For the composite function [latex]g\circ f[/latex], we have [latex](g\circ f)(1)=4, \, (g\circ f)(2)=5,[/latex] and [latex](g\circ f)(3)=4[/latex].

When composing functions, don’t forget to work from the inside out. Also, keep in mind that in general,  [latex]f\left(g\left(x\right)\right)\ne g\left(f\left(x\right)\right)[/latex] for all [latex]x[/latex].

Recall: How to perform a composition of functions

It is important to understand the order of operations in evaluating a composite function. We follow the usual convention with parentheses by starting with the innermost parentheses first, and then working to the outside.

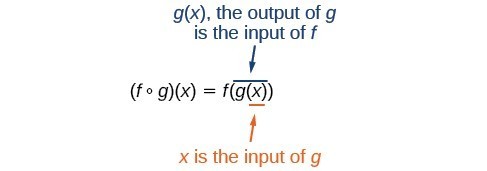
Explanation of the composite function. g(x), the output of g is the input of f. X is the input of g.

In general [latex]f\circ g[/latex] and [latex]g\circ f[/latex] are different functions. In other words in many cases [latex]f\left(g\left(x\right)\right)\ne g\left(f\left(x\right)\right)[/latex] for all [latex]x[/latex].

For example if [latex]f\left(x\right)={x}^{2}[/latex] and [latex]g\left(x\right)=x+2[/latex], then

[latex]\begin{align}f\left(g\left(x\right)\right)&=f\left(x+2\right) \\[2mm] &={\left(x+2\right)}^{2} \\[2mm] &={x}^{2}+4x+4\hfill \end{align}[/latex]

but

[latex]\begin{align}g\left(f\left(x\right)\right)&=g\left({x}^{2}\right) \\[2mm] \text{ }&={x}^{2}+2\hfill \end{align}[/latex]

Example: Compositions of Functions Defined by Formulas

Consider the functions [latex]f(x)=x^2+1[/latex] and [latex]g(x)=\frac{1}{x}[/latex].

  1. Find [latex](g\circ f)(x)[/latex] and state its domain and range.
  2. Evaluate [latex](g\circ f)(4)[/latex] and [latex](g\circ f)\left(-\frac{1}{2}\right)[/latex].
  3. Find [latex](f\circ g)(x)[/latex] and state its domain and range.
  4. Evaluate [latex](f\circ g)(4)[/latex] and [latex](f\circ g)\left(-\frac{1}{2}\right)[/latex].

In the box above, we can see that [latex](f\circ g)(x)\ne (g\circ f)(x)[/latex]. This tells us, in general terms, that the order in which we compose functions matters.

Try It

Let [latex]f(x)=2-5x[/latex]

Let [latex]g(x)=\sqrt{x}[/latex]

Find [latex](f\circ g)(x)[/latex]

 

Example: Composition of Functions Defined by Tables

Consider the functions [latex]f[/latex] and [latex]g[/latex] described below.

[latex]\mathbf{x}[/latex] -3 -2 -1 0 1 2 3 4
[latex]\mathbf{f(x)}[/latex] 0 4 2 4 -2 0 -2 4
[latex]\mathbf{x}[/latex] -4 -2 0 2 4
[latex]\mathbf{g(x)}[/latex] 1 0 3 0 5
  1. Evaluate [latex](g\circ f)(3)[/latex] and [latex](g\circ f)(0)[/latex].
  2. State the domain and range of [latex](g\circ f)(x)[/latex].
  3. Evaluate [latex](f\circ f)(3)[/latex] and [latex](f\circ f)(1)[/latex].
  4. State the domain and range of [latex](f\circ f)(x)[/latex].

Watch the following video to see the worked solution to Example: Composition of Functions Defined by Tables

Example: Application Involving a Composite Function

A store is advertising a sale of [latex]20\%[/latex] off all merchandise. Caroline has a coupon that entitles her to an additional [latex]15\%[/latex] off any item, including sale merchandise. If Caroline decides to purchase an item with an original price of [latex]x[/latex] dollars, how much will she end up paying if she applies her coupon to the sale price? Solve this problem by using a composite function.

Try It

If items are on sale for [latex]10\%[/latex] off their original price, and a customer has a coupon for an additional [latex]30\%[/latex] off, what will be the final price for an item that is originally [latex]x[/latex] dollars, after applying the coupon to the sale price?

 

 

Try It