Differentials and Amount of Error

Learning Outcomes

Draw a graph that illustrates the use of differentials to approximate the change in a quantity
Calculate the relative error and percentage error in using a differential approximation

Computing Differentials

We have seen that linear approximations can be used to estimate function values. They can also be used to estimate the amount a function value changes as a result of a small change in the input. To discuss this more formally, we define a related concept: differentials. Differentials provide us with a way of estimating the amount a function changes as a result of a small change in input values.

When we first looked at derivatives, we used the Leibniz notation $dy/dx$ to represent the derivative of $y$ with respect to $x$ . Although we used the expressions $dy$ and $dx$ in this notation, they did not have meaning on their own. Here we see a meaning to the expressions $dy$ and $dx$ . Suppose $y=f(x)$ is a differentiable function. Let $dx$ be an independent variable that can be assigned any nonzero real number, and define the dependent variable $dy$ by

d y = f^{'} (x) d x

$dy=f^{\prime}(x) \, dx$

It is important to notice that $dy$ is a function of both $x$ and $dx$ . The expressions $dy$ and $dx$ are called differentials. We can divide both sides of the equation by $dx$ , which yields

\frac{d y}{d x} = f^{'} (x)

$\frac{dy}{dx}=f^{\prime}(x)$

This is the familiar expression we have used to denote a derivative. The first equation is known as the differential form of the second one.

Example: Computing differentials

For each of the following functions, find $dy$ and evaluate when $x=3$ and $dx=0.1$ .

$y=x^2+2x$
$y= \cos x$

Show Solution

The key step is calculating the derivative. When we have that, we can obtain $dy$ directly.

Since $f(x)=x^2+2x$ , we know $f^{\prime}(x)=2x+2$ , and therefore
$dy=(2x+2) \, dx$ .

When $x=3$ and $dx=0.1$ ,

$dy=(2 \cdot 3+2)(0.1)=0.8$ .
Since $f(x)= \cos x$ , $f^{\prime}(x)=−\sin (x)$ . This gives us
$dy=−\sin x \, dx$ .

When $x=3$ and $dx=0.1$ ,

$dy=−\sin (3)(0.1)=-0.1 \sin (3)$ .

Watch the following video to see the worked solution to Example: Computing differentials.

Closed Captioning and Transcript Information for Video

Try It

For $y=e^{x^2}$ , find $dy$ .

Hint

$dy=f^{\prime}(x)dx$

Show Solution

$dy=2xe^{x^2} \, dx$

We now connect differentials to linear approximations. Differentials can be used to estimate the change in the value of a function resulting from a small change in input values. Consider a function $f$ that is differentiable at point $a$ . Suppose the input $x$ changes by a small amount. We are interested in how much the output $y$ changes. If $x$ changes from $a$ to $a+dx$ , then the change in $x$ is $dx$ (also denoted $\Delta x$ ), and the change in $y$ is given by

Δ y = f (a + d x) - f (a)

$\Delta y=f(a+dx)-f(a)$

Instead of calculating the exact change in $y$ , however, it is often easier to approximate the change in $y$ by using a linear approximation. For $x$ near $a$ , $f(x)$ can be approximated by the linear approximation

L (x) = f (a) + f^{'} (a) (x - a)

$L(x)=f(a)+f^{\prime}(a)(x-a)$

Therefore, if $dx$ is small,

f (a + d x) \approx L (a + d x) = f (a) + f^{'} (a) (a + d x - a)

$f(a+dx)\approx L(a+dx)=f(a)+f^{\prime}(a)(a+dx-a)$

That is,

f (a + d x) - f (a) \approx L (a + d x) - f (a) = f^{'} (a) d x .

$f(a+dx)-f(a)\approx L(a+dx)-f(a)=f^{\prime}(a) \, dx.$

In other words, the actual change in the function $f$ if $x$ increases from $a$ to $a+dx$ is approximately the difference between $L(a+dx)$ and $f(a)$ , where $L(x)$ is the linear approximation of $f$ at $a$ . By definition of $L(x)$ , this difference is equal to $f^{\prime}(a)dx$ . In summary,

Δ y = f (a + d x) - f (a) \approx L (a + d x) - f (a) = f^{'} (a) d x = d y

$\Delta y=f(a+dx)-f(a)\approx L(a+dx)-f(a)=f^{\prime}(a) \, dx=dy$

Therefore, we can use the differential $dy=f^{\prime}(a) \, dx$ to approximate the change in $y$ if $x$ increases from $x=a$ to $x=a+dx$ . We can see this in the following graph.

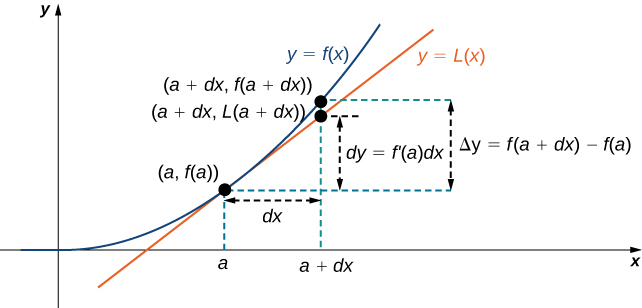
A function y = f(x) is shown along with its tangent line at (a, f(a)). The tangent line is denoted L(x). The x axis is marked with a and a + dx, with a dashed line showing the distance between a and a + dx as dx. The points (a + dx, f(a + dx)) and (a + dx, L(a + dx)) are marked on the curves for y = f(x) and y = L(x), respectively. The distance between f(a) and L(a + dx) is marked as dy = f’(a) dx, and the distance between f(a) and f(a + dx) is marked as Δy = f(a + dx) – f(a).

Figure 5. The differential $dy=f^{\prime}(a) \, dx$ is used to approximate the actual change in $y$ if $x$ increases from $a$ to $a+dx$ .

We now take a look at how to use differentials to approximate the change in the value of the function that results from a small change in the value of the input. Note the calculation with differentials is much simpler than calculating actual values of functions and the result is very close to what we would obtain with the more exact calculation.

Example: Approximating Change with Differentials

Let $y=x^2+2x$ .

Compute $\Delta y$ and $dy$ at $x=3$ if $dx=0.1$ .

Show Solution

The actual change in $y$ if $x$ changes from $x=3$ to $x=3.1$ is given by

Δ y = f (3.1) - f (3) = [(3.1)^{2} + 2 (3.1)] - [3^{2} + 2 (3)] = 0.81

$\Delta y=f(3.1)-f(3)=[(3.1)^2+2(3.1)]-[3^2+2(3)]=0.81$

The approximate change in $y$ is given by $dy=f^{\prime}(3) \, dx$ . Since $f^{\prime}(x)=2x+2$ , we have

d y = f^{'} (3) d x = (2 (3) + 2) (0.1) = 0.8

$dy=f^{\prime}(3) \, dx=(2(3)+2)(0.1)=0.8$ .

Try It

For $y=x^2+2x$ , find $\Delta y$ and $dy$ at $x=3$ if $dx=0.2$ .

Hint

$dy=f^{\prime}(3) \, dx$ , $\Delta y=f(3.2)-f(3)$

Show Solution

$dy=1.6$ , $\Delta y=1.64$

Calculating the Amount of Error

Any type of measurement is prone to a certain amount of error. In many applications, certain quantities are calculated based on measurements. For example, the area of a circle is calculated by measuring the radius of the circle. An error in the measurement of the radius leads to an error in the computed value of the area. Here we examine this type of error and study how differentials can be used to estimate the error.

Consider a function $f$ with an input that is a measured quantity. Suppose the exact value of the measured quantity is $a$ , but the measured value is $a+dx$ . We say the measurement error is $dx$ (or $\Delta x$ ). As a result, an error occurs in the calculated quantity $f(x)$ . This type of error is known as a propagated error and is given by

Δ y = f (a + d x) - f (a)

$\Delta y=f(a+dx)-f(a)$

Since all measurements are prone to some degree of error, we do not know the exact value of a measured quantity, so we cannot calculate the propagated error exactly. However, given an estimate of the accuracy of a measurement, we can use differentials to approximate the propagated error $\Delta y$ . Specifically, if $f$ is a differentiable function at $a$ , the propagated error is

Δ y \approx d y = f^{'} (a) d x

$\Delta y\approx dy=f^{\prime}(a) \, dx$

Unfortunately, we do not know the exact value $a$ . However, we can use the measured value $a+dx$ , and estimate

$\Delta y\approx dy\approx f^{\prime}(a+dx) \, dx$

In the next example, we look at how differentials can be used to estimate the error in calculating the volume of a box if we assume the measurement of the side length is made with a certain amount of accuracy.

Example: Volume of a Cube

Suppose the side length of a cube is measured to be 5 cm with an accuracy of 0.1 cm.

Use differentials to estimate the error in the computed volume of the cube.
Compute the volume of the cube if the side length is (i) 4.9 cm and (ii) 5.1 cm to compare the estimated error with the actual potential error.

Show Solution

The measurement of the side length is accurate to within $\pm 0.1$ cm. Therefore,
$-0.1\le dx\le 0.1$ .

The volume of a cube is given by $V=x^3$ , which leads to

$dV=3x^2 \, dx$ .

Using the measured side length of 5 cm, we can estimate that

$-3(5)^2(0.1)\le dV\le 3(5)^2(0.1)$ .

Therefore,

$-7.5\le dV\le 7.5$ .
If the side length is actually 4.9 cm, then the volume of the cube is
$V(4.9)=(4.9)^3=117.649 \, \text{cm}^3$ .

If the side length is actually 5.1 cm, then the volume of the cube is

$V(5.1)=(5.1)^3=132.651\, \text{cm}^3$ .

Therefore, the actual volume of the cube is between 117.649 and 132.651. Since the side length is measured to be 5 cm, the computed volume is $V(5)=5^3=125$ . Therefore, the error in the computed volume is

$117.649-125\le \Delta V\le 132.651-125$ .

That is,

$-7.351\le \Delta V\le 7.651$ .

We see the estimated error $dV$ is relatively close to the actual potential error in the computed volume.

Watch the following video to see the worked solution to Example: Volume of a Cube.

Closed Captioning and Transcript Information for Video

Try It

Estimate the error in the computed volume of a cube if the side length is measured to be 6 cm with an accuracy of 0.2 cm.

Hint

$dV=3x^2 \, dx$

Show Solution

The volume measurement is accurate to within $21.6 \, \text{cm}^3$ .

The measurement error $dx \, (=\Delta x)$ and the propagated error $\Delta y$ are absolute errors. We are typically interested in the size of an error relative to the size of the quantity being measured or calculated. Given an absolute error $\Delta q$ for a particular quantity, we define the relative error as $\frac{\Delta q}{q}$ , where $q$ is the actual value of the quantity. The percentage error is the relative error expressed as a percentage. For example, if we measure the height of a ladder to be 63 in. when the actual height is 62 in., the absolute error is 1 in. but the relative error is $\frac{1}{62}=0.016$ , or $1.6 \%$ . By comparison, if we measure the width of a piece of cardboard to be 8.25 in. when the actual width is 8 in., our absolute error is $\frac{1}{4}$ in., whereas the relative error is $\frac{0.25}{8}=\frac{1}{32}$ , or $3.1\%$ . Therefore, the percentage error in the measurement of the cardboard is larger, even though 0.25 in. is less than 1 in.

Example: Relative and Percentage Error

An astronaut using a camera measures the radius of Earth as 4000 mi with an error of $\pm 80$ mi. Let’s use differentials to estimate the relative and percentage error of using this radius measurement to calculate the volume of Earth, assuming the planet is a perfect sphere.

Show Solution

If the measurement of the radius is accurate to within $\pm 80$ , we have

$-80\le dr\le 80$ .

Since the volume of a sphere is given by $V=(\frac{4}{3})\pi r^3$ , we have

$dV=4\pi r^2 \, dr$ .

Using the measured radius of 4000 mi, we can estimate

$-4\pi (4000)^2(80)\le dV\le 4\pi (4000)^2(80)$ .

To estimate the relative error, consider $\frac{dV}{V}$ . Since we do not know the exact value of the volume $V$ , use the measured radius $r=4000$ mi to estimate $V$ . We obtain $V\approx (\frac{4}{3})\pi (4000)^3$ . Therefore the relative error satisfies

$\dfrac{-4\pi (4000)^2(80)}{4\pi (4000)^3 / 3}\le \dfrac{dV}{V}\le \dfrac{4\pi (4000)^2(80)}{4\pi (4000)^3 /3}$ ,

which simplifies to

$-0.06\le \frac{dV}{V}\le 0.06$ .

The relative error is 0.06 and the percentage error is $6 \%$ .

Try It

Determine the percentage error if the radius of Earth is measured to be 3950 mi with an error of $\pm 100$ mi.

Hint

Use the fact that $dV=4\pi r^2 \, dr$ to find $dV/V$ .

Show Solution

Module 4: Applications of Derivatives