Infinite Limits

Learning Outcomes

  • Using correct notation, describe an infinite limit
  • Define a vertical asymptote

Evaluating the limit of a function at a point or evaluating the limit of a function from the right and left at a point helps us to characterize the behavior of a function around a given value. As we shall see, we can also describe the behavior of functions that do not have finite limits.

We now turn our attention to [latex]h(x)=\frac{1}{(x-2)^2}[/latex]. From its graph we see that as the values of [latex]x[/latex] approach 2, the values of [latex]h(x)=\frac{1}{(x-2)^2}[/latex] become larger and larger and, in fact, become infinite. Mathematically, we say that the limit of [latex]h(x)[/latex] as [latex]x[/latex] approaches 2 is positive infinity. Symbolically, we express this idea as

[latex]\underset{x\to 2}{\lim}h(x)=+\infty [/latex]

 

More generally, we define infinite limits as follows:

Definition

We define three types of infinite limits.

Infinite limits from the left: Let [latex]f(x)[/latex] be a function defined at all values in an open interval of the form [latex](b,a)[/latex].

  1. If the values of [latex]f(x)[/latex] increase without bound as the values of [latex]x[/latex] (where [latex]x<a[/latex]) approach the number [latex]a[/latex], then we say that the limit as [latex]x[/latex] approaches [latex]a[/latex] from the left is positive infinity and we write
    [latex]\underset{x\to a^-}{\lim}f(x)=+\infty[/latex].
  2. If the values of [latex]f(x)[/latex] decrease without bound as the values of [latex]x[/latex] (where [latex]x<a[/latex]) approach the number [latex]a[/latex], then we say that the limit as [latex]x[/latex] approaches [latex]a[/latex] from the left is negative infinity and we write
    [latex]\underset{x\to a^-}{\lim}f(x)=−\infty[/latex].

Infinite limits from the right: Let [latex]f(x)[/latex] be a function defined at all values in an open interval of the form [latex](a,c)[/latex].

  1. If the values of [latex]f(x)[/latex] increase without bound as the values of [latex]x[/latex] (where [latex]x>a[/latex]) approach the number [latex]a[/latex], then we say that the limit as [latex]x[/latex] approaches [latex]a[/latex] from the right is positive infinity and we write
    [latex]\underset{x\to a^+}{\lim}f(x)=+\infty[/latex].
  2. If the values of [latex]f(x)[/latex] decrease without bound as the values of [latex]x[/latex] (where [latex]x>a[/latex]) approach the number [latex]a[/latex], then we say that the limit as [latex]x[/latex] approaches [latex]a[/latex] from the right is negative infinity and we write
    [latex]\underset{x\to a^+}{\lim}f(x)=−\infty[/latex].

Two-sided infinite limit: Let [latex]f(x)[/latex] be defined for all [latex]x\ne a[/latex] in an open interval containing [latex]a[/latex].

  1. If the values of [latex]f(x)[/latex] increase without bound as the values of [latex]x[/latex] (where [latex]x\ne a[/latex]) approach the number [latex]a[/latex], then we say that the limit as [latex]x[/latex] approaches [latex]a[/latex] is positive infinity and we write
    [latex]\underset{x\to a}{\lim}f(x)=+\infty[/latex].
  2. If the values of [latex]f(x)[/latex] decrease without bound as the values of [latex]x[/latex] (where [latex]x\ne a[/latex]) approach the number [latex]a[/latex], then we say that the limit as [latex]x[/latex] approaches [latex]a[/latex] is negative infinity and we write
    [latex]\underset{x\to a}{\lim}f(x)=−\infty[/latex].

Try It

It is important to understand that when we write statements such as [latex]\underset{x\to a}{\lim}f(x)=+\infty [/latex] or [latex]\underset{x\to a}{\lim}f(x)=−\infty [/latex] we are describing the behavior of the function, as we have just defined it. We are not asserting that a limit exists. For the limit of a function [latex]f(x)[/latex] to exist at [latex]a[/latex], it must approach a real number [latex]L[/latex] as [latex]x[/latex] approaches [latex]a[/latex]. That said, if, for example, [latex]\underset{x\to a}{\lim}f(x)=+\infty[/latex], we always write [latex]\underset{x\to a}{\lim}f(x)=+\infty [/latex] rather than [latex]\underset{x\to a}{\lim}f(x)[/latex] DNE.

Example: Recognizing an Infinite Limit

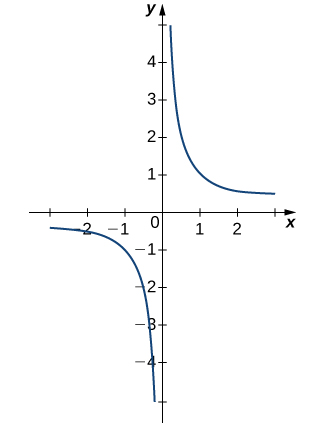
Evaluate each of the following limits, if possible. Use a table of functional values and graph [latex]f(x)=1/x[/latex] to confirm your conclusion.

  1. [latex]\underset{x\to 0^-}{\lim}\frac{1}{x}[/latex]
  2. [latex]\underset{x\to 0^+}{\lim}\frac{1}{x}[/latex]
  3. [latex]\underset{x\to 0}{\lim}\frac{1}{x}[/latex]

Try It

Evaluate each of the following limits, if possible. Use a table of functional values and graph [latex]f(x)=\dfrac{1}{x^2}[/latex] to confirm your conclusion.

  1. [latex]\underset{x\to 0^-}{\lim}\frac{1}{x^2}[/latex]
  2. [latex]\underset{x\to 0^+}{\lim}\frac{1}{x^2}[/latex]
  3. [latex]\underset{x\to 0}{\lim}\frac{1}{x^2}[/latex]

It is useful to point out that functions of the form [latex]f(x)=\dfrac{1}{(x-a)^n}[/latex], where [latex]n[/latex] is a positive integer, have infinite limits as [latex]x[/latex] approaches [latex]a[/latex] from either the left or right (Figure 9). These limits are summarized below the graphs.

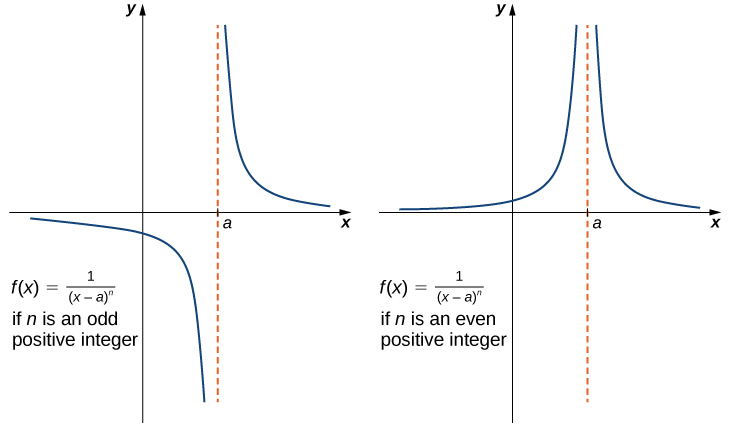
Two graphs side by side of f(x) = 1 / (x-a)^n. The first graph shows the case where n is an odd positive integer, and the second shows the case where n is an even positive integer. In the first, the graph has two segments. Each curve asymptotically towards the x axis, also known as y=0, and x=a. The segment to the left of x=a is below the x axis, and the segment to the right of x=a is above the x axis. In the second graph, both segments are above the x axis.

Figure 9. The function [latex]f(x)=1/(x-a)^n[/latex] has infinite limits at [latex]a[/latex].

Infinite Limits from Positive Integers

If [latex]n[/latex] is a positive even integer, then

[latex]\underset{x\to a}{\lim}\dfrac{1}{(x-a)^n}=+\infty[/latex]

 

If [latex]n[/latex] is a positive odd integer, then

[latex]\underset{x\to a^+}{\lim}\dfrac{1}{(x-a)^n}=+\infty [/latex]

 

and

[latex]\underset{x\to a^-}{\lim}\dfrac{1}{(x-a)^n}=−\infty[/latex]

We should also point out that in the graphs of [latex]f(x)=\dfrac{1}{(x-a)^n}[/latex], points on the graph having [latex]x[/latex]-coordinates very near to [latex]a[/latex] are very close to the vertical line [latex]x=a[/latex]. That is, as [latex]x[/latex] approaches [latex]a[/latex], the points on the graph of [latex]f(x)[/latex] are closer to the line [latex]x=a[/latex]. The line [latex]x=a[/latex] is called a vertical asymptote of the graph. We formally define a vertical asymptote as follows:

Definition

Let [latex]f(x)[/latex] be a function. If any of the following conditions hold, then the line [latex]x=a[/latex] is a vertical asymptote of [latex]f(x)[/latex]:

[latex]\begin{array}{ccc}\hfill \underset{x\to a^-}{\lim}f(x)& =\hfill & +\infty \, \text{or} \, -\infty \hfill \\ \hfill \underset{x\to a^+}{\lim}f(x)& =\hfill & +\infty \, \text{or} \, −\infty \hfill \\ & \text{or}\hfill & \\ \hfill \underset{x\to a}{\lim}f(x)& =\hfill & +\infty \, \text{or} \, −\infty \hfill \end{array}[/latex]

Example: Finding a Vertical Asymptote

Evaluate each of the following limits using the limits summarized under Figure 9. Identify any vertical asymptotes of the function [latex]f(x)=\dfrac{1}{(x+3)^4}[/latex].

  1. [latex]\underset{x\to -3^-}{\lim}\dfrac{1}{(x+3)^4}[/latex]
  2. [latex]\underset{x\to -3^+}{\lim}\dfrac{1}{(x+3)^4}[/latex]
  3. [latex]\underset{x\to -3}{\lim}\dfrac{1}{(x+3)^4}[/latex]

Watch the following video to see the more examples of finding a vertical asymptote.

Try It

Evaluate each of the following limits. Identify any vertical asymptotes of the function [latex]f(x)=\dfrac{1}{(x-2)^3}[/latex].

  1. [latex]\underset{x\to 2^-}{\lim}\dfrac{1}{(x-2)^3}[/latex]
  2. [latex]\underset{x\to 2^+}{\lim}\dfrac{1}{(x-2)^3}[/latex]
  3. [latex]\underset{x\to 2}{\lim}\dfrac{1}{(x-2)^3}[/latex]

In the next example, we put our knowledge of various types of limits to use to analyze the behavior of a function at several different points.

Example: Behavior of a Function at Different Points

Use the graph of [latex]f(x)[/latex] in Figure 10 to determine each of the following values:

  1. [latex]\underset{x\to -4^-}{\lim}f(x); \, \underset{x\to -4^+}{\lim}f(x); \, \underset{x\to -4}{\lim}f(x); \, f(-4)[/latex]
  2. [latex]\underset{x\to -2^-}{\lim}f(x); \, \underset{x\to -2^+}{\lim}f(x); \, \underset{x\to -2}{\lim}f(x); \, f(-2)[/latex]
  3. [latex]\underset{x\to 1^-}{\lim}f(x); \, \underset{x\to 1^+}{\lim}f(x); \, \underset{x\to 1}{\lim}f(x); \, f(1)[/latex]
    The graph of a function f(x) described by the above limits and values. There is a smooth curve for values below x=-2; at (-2, 3), there is an open circle. There is a smooth curve between (-2, 1] with a closed circle at (1,6). There is an open circle at (1,3), and a smooth curve stretching from there down asymptotically to negative infinity along x=3. The function also curves asymptotically along x=3 on the other side, also stretching to negative infinity. The function then changes concavity in the first quadrant around y=4.5 and continues up.

    Figure 10. The graph shows [latex]f(x)[/latex].

Watch the following video to see the worked solution to Example: Behavior of a Function at Different Points. Note this video also repeats the steps for x = 3.

Try It

Evaluate [latex]\underset{x\to 1}{\lim}f(x)[/latex] for [latex]f(x)[/latex] shown here:

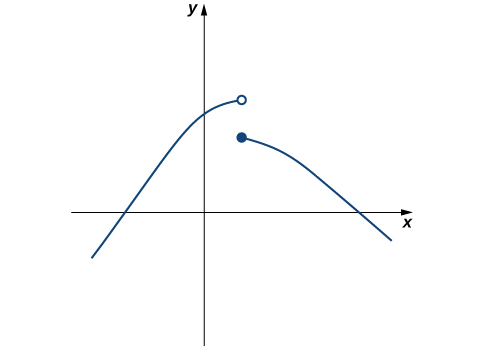
A graph of a piecewise function. The first segment curves from the third quadrant to the first, crossing through the second quadrant. Where the endpoint would be in the first quadrant is an open circle. The second segment starts at a closed circle a few units below the open circle. It curves down from quadrant one to quadrant four.

Figure 11.

Try It