Learning Outcomes
- Define one-sided limits and provide examples
- Explain the relationship between one-sided and two-sided limits
Sometimes indicating that the limit of a function fails to exist at a point does not provide us with enough information about the behavior of the function at that particular point. To see this, we now revisit the function [latex]g(x)=\frac{|x-2|}{(x-2)}[/latex] introduced at the beginning of the section. As we pick values of [latex]x[/latex] close to 2, [latex]g(x)[/latex] does not approach a single value, so the limit as [latex]x[/latex] approaches 2 does not exist—that is, [latex]\underset{x\to 2}{\lim}g(x)[/latex] DNE. However, this statement alone does not give us a complete picture of the behavior of the function around the [latex]x[/latex]-value 2. To provide a more accurate description, we introduce the idea of a one-sided limit. For all values to the left of 2 (or the negative side of 2), [latex]g(x)=-1[/latex]. Thus, as [latex]x[/latex] approaches 2 from the left, [latex]g(x)[/latex] approaches −1. Mathematically, we say that the limit as [latex]x[/latex] approaches 2 from the left is −1. Symbolically, we express this idea as
Similarly, as [latex]x[/latex] approaches 2 from the right (or from the positive side), [latex]g(x)[/latex] approaches 1. Symbolically, we express this idea as
We can now present an informal definition of one-sided limits.
Definition
We define two types of one-sided limits.
Limit from the left: Let [latex]f(x)[/latex] be a function defined at all values in an open interval of the form [latex](c,a)[/latex], and let [latex]L[/latex] be a real number. If the values of the function [latex]f(x)[/latex] approach the real number [latex]L[/latex] as the values of [latex]x[/latex] (where [latex]x<a[/latex]) approach the number [latex]a[/latex], then we say that [latex]L[/latex] is the limit of [latex]f(x)[/latex] as [latex]x[/latex] approaches [latex]a[/latex] from the left. Symbolically, we express this idea as
Limit from the right: Let [latex]f(x)[/latex] be a function defined at all values in an open interval of the form [latex](a,c)[/latex], and let [latex]L[/latex] be a real number. If the values of the function [latex]f(x)[/latex] approach the real number [latex]L[/latex] as the values of [latex]x[/latex] (where [latex]x>a[/latex]) approach the number [latex]a[/latex], then we say that [latex]L[/latex] is the limit of [latex]f(x)[/latex] as [latex]x[/latex] approaches [latex]a[/latex] from the right. Symbolically, we express this idea as
Example: Evaluating One-Sided Limits
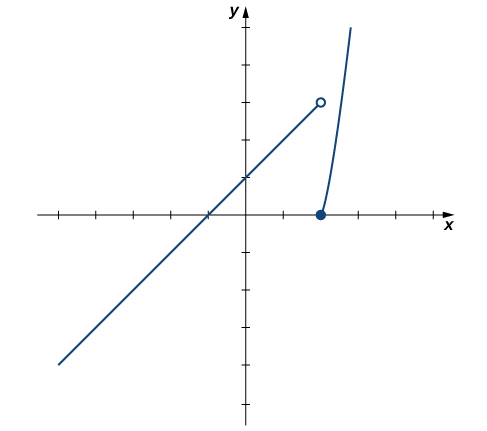
For the function [latex]f(x)=\begin{cases} x+1, & \text{ if } \, x < 2 \\ x^2-4, & \text{ if } \, x \ge 2 \end{cases}[/latex], evaluate each of the following limits.
- [latex]\underset{x\to 2^-}{\lim}f(x)[/latex]
- [latex]\underset{x\to 2^+}{\lim}f(x)[/latex]
Watch the following video to see the worked solution to Example: Evaluating One-Sided Limits
Try It
Use a table of functional values to estimate the following limits, if possible.
- [latex]\underset{x\to 2^-}{\lim}\dfrac{|x^2-4|}{x-2}[/latex]
- [latex]\underset{x\to 2^+}{\lim}\dfrac{|x^2-4|}{x-2}[/latex]
Try It
Let us now consider the relationship between the limit of a function at a point and the limits from the right and left at that point. It seems clear that if the limit from the right and the limit from the left have a common value, then that common value is the limit of the function at that point. Similarly, if the limit from the left and the limit from the right take on different values, the limit of the function does not exist.
Relating One-Sided and Two-Sided Limits
Let [latex]f(x)[/latex] be a function defined at all values in an open interval containing [latex]a[/latex], with the possible exception of [latex]a[/latex] itself, and let [latex]L[/latex] be a real number. Then,
[latex]\underset{x\to a}{\lim}f(x)=L[/latex], if and only if [latex]\underset{x\to a^-}{\lim}f(x)=L[/latex] and [latex]\underset{x\to a^+}{\lim}f(x)=L[/latex]