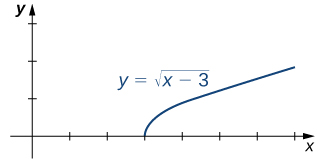Learning Outcomes
- Evaluate the limit of a function by factoring
- Use the limit laws to evaluate the limit of a polynomial or rational function
- Evaluate the limit of a function by factoring or by using conjugates
As we have seen, we may evaluate easily the limits of polynomials and limits of some (but not all) rational functions by direct substitution. However, as we saw in the introductory section on limits, it is certainly possible for [latex]\underset{x\to a}{\lim}f(x)[/latex] to exist when [latex]f(a)[/latex] is undefined. The following observation allows us to evaluate many limits of this type:
If for all [latex]x\ne a, \, f(x)=g(x)[/latex] over some open interval containing [latex]a[/latex], then [latex]\underset{x\to a}{\lim}f(x)=\underset{x\to a}{\lim}g(x)[/latex].
To understand this idea better, consider the limit [latex]\underset{x\to 1}{\lim}\frac{x^2-1}{x-1}[/latex].
The function
and the function [latex]g(x)=x+1[/latex] are identical for all values of [latex]x\ne 1.[/latex] The graphs of these two functions are shown in Figure 1.

Figure 1. The graphs of [latex]f(x)[/latex] and [latex]g(x)[/latex] are identical for all [latex]x\ne 1[/latex]. Their limits at 1 are equal.
We see that
The limit has the form [latex]\underset{x\to a}{\lim}\frac{f(x)}{g(x)}[/latex], where [latex]\underset{x\to a}{\lim}f(x)=0[/latex] and [latex]\underset{x\to a}{\lim}g(x)=0[/latex]. (In this case, we say that [latex]\frac{f(x)}{g(x)}[/latex] has the indeterminate form [latex]\frac{0}{0}[/latex].) The following Problem-Solving Strategy provides a general outline for evaluating limits of this type.
Problem-Solving Strategy: Calculating a Limit When [latex]f(x)/g(x)[/latex] has the Indeterminate Form 0/0
- First, we need to make sure that our function has the appropriate form and cannot be evaluated immediately using the limit laws.
- We then need to find a function that is equal to [latex]h(x)=f(x)/g(x)[/latex] for all [latex]x\ne a[/latex] over some interval containing [latex]a[/latex]. To do this, we may need to try one or more of the following steps:
- If [latex]f(x)[/latex] and [latex]g(x)[/latex] are polynomials, we should factor each function and cancel out any common factors.
- If the numerator or denominator contains a difference involving a square root, we should try multiplying the numerator and denominator by the conjugate of the expression involving the square root.
- If [latex]f(x)/g(x)[/latex] is a complex fraction, we begin by simplifying it.
- Last, we apply the limit laws.
The next examples demonstrate the use of this Problem-Solving Strategy. It may be helpful to revisit the following algebraic techniques.
Recall: Factoring polynomials
Key Equations
| difference of squares | [latex]{a}^{2}-{b}^{2}=\left(a+b\right)\left(a-b\right)[/latex] |
| perfect square trinomial | [latex]{a}^{2}+2ab+{b}^{2}={\left(a+b\right)}^{2}[/latex] |
| sum of cubes | [latex]{a}^{3}+{b}^{3}=\left(a+b\right)\left({a}^{2}-ab+{b}^{2}\right)[/latex] |
| difference of cubes | [latex]{a}^{3}-{b}^{3}=\left(a-b\right)\left({a}^{2}+ab+{b}^{2}\right)[/latex] |
Key Concepts
- The greatest common factor, or GCF, can be factored out of a polynomial. Checking for a GCF should be the first step in any factoring problem.
- Trinomials with leading coefficient 1 can be factored by finding numbers that have a product of the third term and a sum of the second term.
- Trinomials can be factored using a process called factoring by grouping.
- Perfect square trinomials and the difference of squares are special products and can be factored using equations.
- The sum of cubes and the difference of cubes can be factored using equations.
- Polynomials containing fractional and negative exponents can be factored by pulling out a GCF.
- factor by grouping
- a method for factoring a trinomial of the form [latex]a{x}^{2}+bx+c[/latex] by dividing the x term into the sum of two terms, factoring each portion of the expression separately, and then factoring out the GCF of the entire expression
- greatest common factor
- the largest polynomial that divides evenly into each polynomial
Recall: The conjugate of a sum or difference of a rational and irrational term
The conjugate of the sum or difference of a rational and an irrational term can be found by changing the sign of the radical portion of the denominator. If the denominator is [latex]a+b\sqrt{c}[/latex], then the conjugate is [latex]a-b\sqrt{c}[/latex].
The example below illustrates the factor-and-cancel technique; the next shows multiplying by a conjugate. In the one after that, we look at simplifying a complex fraction.
Example: Evaluating a Limit by Factoring and Canceling
Evaluate [latex]\underset{x\to 3}{\lim}\dfrac{x^2-3x}{2x^2-5x-3}[/latex]
Try It
Evaluate [latex]\underset{x\to -3}{\lim}\dfrac{x^2+4x+3}{x^2-9}[/latex]
Watch the following video to see the worked solution to the above Try It as well as another worked example of evaluating a limit by factoring and canceling.
Try It
Try It
Example: Evaluating a Limit by Multiplying by a Conjugate
Evaluate [latex]\underset{x\to -1}{\lim}\dfrac{\sqrt{x+2}-1}{x+1}[/latex]
Try It
Evaluate [latex]\underset{x\to 5}{\lim}\dfrac{\sqrt{x-1}-2}{x-5}[/latex]
The next few examples involve complex fractions that will require combining rational expressions to simplify complex fractions.
Recall: Given two rational expressions, add or subtract them
- Factor the numerator and denominator.
- Find the LCD of the expressions.
- Multiply the expressions by a form of 1 that changes the denominators to the LCD.
- Add or subtract the numerators.
- Simplify.
Example:
First, we have to find the LCD. In this case, the LCD will be [latex]xy[/latex]. We then multiply each expression by the appropriate form of 1 to obtain [latex]xy[/latex] as the denominator for each fraction.
Now that the expressions have the same denominator, we simply add the numerators to find the sum.
Recall: Given a complex rational expression, simplify it
- Combine the expressions in the numerator into a single rational expression by adding or subtracting.
- Combine the expressions in the denominator into a single rational expression by adding or subtracting.
- Rewrite as the numerator divided by the denominator.
- Rewrite as multiplication.
- Multiply.
- Simplify.
Example: [latex]\dfrac{y+\dfrac{1}{x}}{\dfrac{x}{y}}[/latex] .Begin by combining the expressions in the numerator into one expression.[latex]\begin{array}{cc}y\cdot \dfrac{x}{x}+\dfrac{1}{x}\hfill & \text{Multiply by }\dfrac{x}{x}\text{to get LCD as denominator}.\hfill \\ \dfrac{xy}{x}+\dfrac{1}{x}\hfill & \\ \dfrac{xy+1}{x}\hfill & \text{Add numerators}.\hfill \end{array}[/latex]Now the numerator is a single rational expression and the denominator is a single rational expression.
[latex]\dfrac{\dfrac{xy+1}{x}}{\dfrac{x}{y}}[/latex]We can rewrite this as division and then multiplication.
[latex]\begin{array}{cc}\dfrac{xy+1}{x}\div \dfrac{x}{y}\hfill & \\ \dfrac{xy+1}{x}\cdot \dfrac{y}{x}\hfill & \text{Rewrite as multiplication}\text{.}\hfill \\ \dfrac{y\left(xy+1\right)}{{x}^{2}}\hfill & \text{Multiply}\text{.}\hfill \end{array}[/latex]
Example: Evaluating a Limit by Simplifying a Complex Fraction
Evaluate [latex]\underset{x\to 1}{\lim}\dfrac{\frac{1}{x+1}-\frac{1}{2}}{x-1}[/latex]
Try It
Evaluate [latex]\underset{x\to -3}{\lim}\dfrac{\frac{1}{x+2}+1}{x+3}[/latex]
Watch the following video to see the worked solution to the above Try It.
The example below does not fall neatly into any of the patterns established in the previous examples. However, with a little creativity, we can still use these same techniques.
Example: Evaluating a Limit When the Limit Laws Do Not Apply
Evaluate [latex]\underset{x\to 0}{\lim}\left(\dfrac{1}{x}+\dfrac{5}{x(x-5)}\right)[/latex]
Try It
Evaluate [latex]\underset{x\to 3}{\lim}\left(\dfrac{1}{x-3}-\dfrac{4}{x^2-2x-3}\right)[/latex]
Simple modifications in the limit laws allow us to apply them to one-sided limits. For example, to apply the limit laws to a limit of the form [latex]\underset{x\to a^-}{\lim}h(x)[/latex], we require the function [latex]h(x)[/latex] to be defined over an open interval of the form [latex](b,a)[/latex]; for a limit of the form [latex]\underset{x\to a^+}{\lim}h(x)[/latex], we require the function [latex]h(x)[/latex] to be defined over an open interval of the form [latex](a,c)[/latex]. The example illustrates this point.
Example: Evaluating a One-Sided Limit Using the Limit Laws
Evaluate each of the following limits, if possible.
- [latex]\underset{x\to 3^-}{\lim}\sqrt{x-3}[/latex]
- [latex]\underset{x\to 3^+}{\lim}\sqrt{x-3}[/latex]
In the example below, we look at one-sided limits of a piecewise-defined function and use these limits to draw a conclusion about a two-sided limit of the same function.
Example: Evaluating a Two-Sided Limit Using the Limit Laws
For [latex]f(x)=\begin{cases} 4x-3 & \text{ if } \, x<2 \\ (x-3)^2 & \text{ if } \, x \ge 2 \end{cases}[/latex] evaluate each of the following limits:
- [latex]\underset{x\to 2^-}{\lim}f(x)[/latex]
- [latex]\underset{x\to 2^+}{\lim}f(x)[/latex]
- [latex]\underset{x\to 2}{\lim}f(x)[/latex]
Try It
Graph [latex]f(x)=\begin{cases} -x-2 & \text{ if } \, x<-1 \\ 2 & \text{ if } \, x = -1 \\ x^3 & \text{ if } \, x > -1 \end{cases}[/latex] and evaluate [latex]\underset{x\to -1^-}{\lim}f(x)[/latex]
We now turn our attention to evaluating a limit of the form [latex]\underset{x\to a}{\lim}\frac{f(x)}{g(x)}[/latex], where [latex]\underset{x\to a}{\lim}f(x) = K[/latex], where [latex]K\ne{0}[/latex] and [latex]\underset{x\to a}{\lim}g(x) = 0[/latex]. That is [latex]f(x)\text{/}g(x)[/latex] has the form [latex]K\text{/}0[/latex], [latex]K\ne{0}[/latex] at [latex]a[/latex].
Example: Evaluating a Limit of the Form [latex]K/0, \, K\ne 0[/latex] Using the Limit Laws
Evaluate [latex]\underset{x\to 2^-}{\lim}\dfrac{x-3}{x^2-2x}[/latex]
Try It
Evaluate [latex]\underset{x\to 1}{\lim}\dfrac{x+2}{(x-1)^2}[/latex]
Candela Citations
- 2.3 Limit Laws. Authored by: Ryan Melton. License: CC BY: Attribution
- Calculus Volume 1. Authored by: Gilbert Strang, Edwin (Jed) Herman. Provided by: OpenStax. Located at: https://openstax.org/details/books/calculus-volume-1. License: CC BY-NC-SA: Attribution-NonCommercial-ShareAlike. License Terms: Access for free at https://openstax.org/books/calculus-volume-1/pages/1-introduction