In the Maxima and Minima and the Mean Value Theorem sections, we will find the domain of functions and their derivatives. Derivatives will also be set equal to 0 or some specific value in both sections which will lead to having to solve various types of equations. Here we will review how to find the domain of functions and how to solve various types of equations.

Find the Domain of a Function

Recall that the domain of a function is all input values where the function is defined. When given a function equation, you must remember the following three cases:

1. If the function has no denominator or an even root, in most cases, the domain will be all real numbers.
2. If there is a denominator in the function’s equation, exclude values in the domain that force the denominator to be zero.
3. If there is an even root, consider excluding values that would make the quantity under the radical negative.

Example: Finding the Domain of a Rational Function

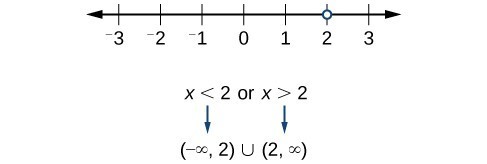
Find the domain of the function [latex]f\left(x\right)=\dfrac{x+1}{2-x}[/latex].

Show Solution

When there is a denominator, we want to include only values of the input that do not force the denominator to be zero. So, we will set the denominator equal to 0 and solve for [latex]x[/latex].

[latex]\begin{align}2-x&=0 \\ -x&=-2 \\ x&=2 \end{align}[/latex]

Now, we will exclude 2 from the domain. The answers are all real numbers where [latex]x<2[/latex] or [latex]x>2[/latex]. We can use a symbol known as the union, [latex]\cup [/latex], to combine the two sets. In interval notation, we write the solution: [latex]\left(\mathrm{-\infty },2\right)\cup \left(2,\infty \right)[/latex].

In interval form, the domain of [latex]f[/latex] is [latex]\left(-\infty ,2\right)\cup \left(2,\infty \right)[/latex].

Watch the following video to see more examples of how to find the domain of a rational function.

You can view the transcript for “Ex: The Domain of Rational Functions” here (opens in new window).

The next video gives more examples of how to define the domain of a function that contains an even root.

You can view the transcript for “Ex: Domain and Range of Square Root Functions” here (opens in new window).

Solve Quadratic Equations by Factoring

(also in Module 3, Skills Review for Differentiation Rules)

Often, the easiest method of solving a quadratic equation is by factoring. When solving a quadratic equation by factoring, you must first set the equation equal to zero, factor, and then set each of the factors equal to 0 and solve for the variable.

Solve Rational Equations Set Equal to Zero

Equations that contain rational expressions are called rational equations. For example, [latex] \frac{2x+1}{4}=\frac{x}{3}[/latex] is a rational equation. Specifically, for the sake of calculus, you will often take derivatives that are rational expressions and set them equal to 0.

As a bit of a hint, almost always, the best way to determine where a rational expression (fraction) is equal to 0 is to set the numerator of the fraction equal to 0.

Solve Radical Equations

An equation that contains a radical expression is called a radical equation. Solving radical equations requires applying the rules of exponents and following some basic algebraic principles. In some cases, it also requires looking out for errors generated by raising unknown quantities to an even power.

To check your solution, you can substitute [latex]64[/latex] in for x in the original equation. Does [latex] \sqrt{64}-3=5[/latex]? Yes—the square root of [latex]64[/latex] is [latex]8[/latex], and [latex]8−3=5[/latex].

Notice how you combined like terms and then squared both sides of the equation in this problem. This is a standard method for removing a radical from an equation. It is important to isolate a radical on one side of the equation and simplify as much as possible before squaring. The fewer terms there are before squaring, the fewer additional terms will be generated by the process of squaring.

In the example above, only the variable x was underneath the radical. Sometimes you will need to solve an equation that contains multiple terms underneath a radical. Follow the same steps to solve these, but pay attention to a critical point—square both sides of an equation, not individual terms.

In the following video, you will see two more examples that are similar to the ones above.

You can view the transcript for “Ex 1: Solve a Basic Radical Equation – Square Roots” here (opens in new window).

Solve Trigonometric Equations

Trigonometric equations are, as the name implies, equations that involve trigonometric functions. We will often solve a trigonometric equation over a specified interval. However, we will sometimes be asked to find all possible solutions, and as trigonometric functions are periodic, solutions are repeated within each period. In other words, trigonometric equations may have an infinite number of solutions. The domain of the function must be considered before we assume that any solution is valid. The period of both the sine function and the cosine function is [latex]2\pi [/latex]. In other words, every [latex]2\pi [/latex] units, the y-values repeat. If we need to find all possible solutions, then we must add [latex]2\pi k[/latex], where [latex]k[/latex] is an integer, to the initial solution.

One quick way to solve trigonometric equations is to use the unit circle. Remember that the unit circle tells us the value of cosine and sine at any of the given angle measures seen below. The first coordinate in each ordered pair is the value of cosine at the given angle measure, while the second coordinate in each ordered pair is the value of sine at the given angle measure.