Learning Outcomes
- Describe the velocity as a rate of change
- Explain the difference between average velocity and instantaneous velocity
- Estimate the derivative from a table of values
Now that we can evaluate a derivative, we can use it in velocity applications. Recall that if [latex]s(t)[/latex] is the position of an object moving along a coordinate axis, the average velocity of the object over a time interval [latex][a,t][/latex] if [latex]t>a[/latex] or [latex][t,a][/latex] if [latex]t As the values of [latex]t[/latex] approach [latex]a[/latex], the values of [latex]v_{\text{avg}}[/latex] approach the value we call the instantaneous velocity at [latex]a[/latex]. That is, instantaneous velocity at [latex]a[/latex], denoted [latex]v(a)[/latex], is given by To better understand the relationship between average velocity and instantaneous velocity, see Figure 7. In this figure, the slope of the tangent line (shown in red) is the instantaneous velocity of the object at time [latex]t=a[/latex] whose position at time [latex]t[/latex] is given by the function [latex]s(t)[/latex]. The slope of the secant line (shown in green) is the average velocity of the object over the time interval [latex][a,t][/latex]. Figure 7. The slope of the secant line is the average velocity over the interval [latex][a,t][/latex]. The slope of the tangent line is the instantaneous velocity. We can use the definitions to calculate the instantaneous velocity, or we can estimate the velocity of a moving object by using a table of values. We can then confirm the estimate by using the difference quotient. A lead weight on a spring is oscillating up and down. Its position at time [latex]t[/latex] with respect to a fixed horizontal line is given by [latex]s(t)= \sin t[/latex]. Use a table of values to estimate [latex]v(0)[/latex]. Check the estimate by using the definition of a derivative. Figure 8. A lead weight suspended from a spring in vertical oscillatory motion. A rock is dropped from a height of 64 feet. Its height above ground at time [latex]t[/latex] seconds later is given by [latex]s(t)=-16t^2+64, \, 0\le t\le 2[/latex]. Find its instantaneous velocity 1 second after it is dropped, using the definition of a derivative. Watch the following video to see the worked solution to the above Try It. As we have seen throughout this section, the slope of a tangent line to a function and instantaneous velocity are related concepts. Each is calculated by computing a derivative and each measures the instantaneous rate of change of a function, or the rate of change of a function at any point along the function. The instantaneous rate of change of a function [latex]f(x)[/latex] at a value [latex]a[/latex] is its derivative [latex]f^{\prime}(a)[/latex]. A homeowner sets the thermostat so that the temperature in the house begins to drop from [latex]70^{\circ}\text{F}[/latex] at 9 p.m., reaches a low of [latex]60^{\circ}[/latex] during the night, and rises back to [latex]70^{\circ}[/latex] by 7 a.m. the next morning. Suppose that the temperature in the house is given by [latex]T(t)=0.4t^2-4t+70[/latex] for [latex]0\le t\le 10[/latex], where [latex]t[/latex] is the number of hours past 9 p.m. Find the instantaneous rate of change of the temperature at midnight. A toy company can sell [latex]x[/latex] electronic gaming systems at a price of [latex]p=-0.01x+400[/latex] dollars per gaming system. The cost of manufacturing [latex]x[/latex] systems is given by [latex]C(x)=100x+10,000[/latex] dollars. Find the rate of change of profit when 10,000 games are produced. Should the toy company increase or decrease production? A coffee shop determines that the daily profit on scones obtained by charging [latex]s[/latex] dollars per scone is [latex]P(s)=-20s^2+150s-10[/latex]. The coffee shop currently charges [latex]\$3.25[/latex] per scone. Find [latex]P^{\prime}(3.25)[/latex], the rate of change of profit when the price is [latex]\$3.25[/latex] and decide whether or not the coffee shop should consider raising or lowering its prices on scones.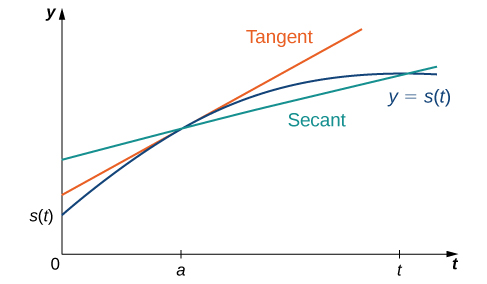
Example: Estimating Velocity
Try It
Definition
Example: Rate of Change of Temperature
Example: Rate of Change of Profit
Try It
Try It
Candela Citations
