Module 3 Review Problems

For the following exercises, determine whether the statement is true or false. Justify your answer with a proof or a counterexample.

\int e^{x} \sin (x) d x

$\displaystyle\int {e}^{x}\sin\left(x\right)dx$ cannot be integrated by parts.

2. $\displaystyle\int \frac{1}{{x}^{4}+1}dx$ cannot be integrated using partial fractions.

Show Solution

3. In numerical integration, increasing the number of points decreases the error.

4. Integration by parts can always yield the integral.

Show Solution

For the following exercises, evaluate the integral using the specified method.

\int x^{2} \sin (4 x) d x

$\displaystyle\int {x}^{2}\sin\left(4x\right)dx$ using integration by parts

6. $\displaystyle\int \frac{1}{{x}^{2}\sqrt{{x}^{2}+16}}dx$ using trigonometric substitution

Show Solution

- \frac{\sqrt{x^{2} + 16}}{16 x} + C

$-\frac{\sqrt{{x}^{2}+16}}{16x}+C$

\int \sqrt{x} ln (x) d x

$\displaystyle\int \sqrt{x}\text{ln}\left(x\right)dx$ using integration by parts

8. $\displaystyle\int \frac{3x}{{x}^{3}+2{x}^{2}-5x - 6}dx$ using partial fractions

Show Solution

\frac{1}{10} (4 ln (2 - x) + 5 ln (x + 1) - 9 ln (x + 3)) + C

$\frac{1}{10}\left(4\text{ln}\left(2-x\right)+5\text{ln}\left(x+1\right)-9\text{ln}\left(x+3\right)\right)+C$

\int \frac{x^{5}}{{(4 x^{2} + 4)}^{\frac{5}{2}}} d x

$\displaystyle\int \frac{{x}^{5}}{{\left(4{x}^{2}+4\right)}^{\frac{5}{2}}}dx$ using trigonometric substitution

10. $\displaystyle\int \frac{\sqrt{4-{\sin}^{2}\left(x\right)}}{{\sin}^{2}\left(x\right)}\cos\left(x\right)dx$ using a table of integrals or a CAS

Show Solution

- \frac{\sqrt{4 - \sin^{2} (x)}}{\sin (x)} - \frac{x}{2} + C

$-\frac{\sqrt{4-{\sin}^{2}\left(x\right)}}{\sin\left(x\right)}-\frac{x}{2}+C$

For the following exercises, integrate using whatever method you choose.

11.

\int \sin^{2} (x) \cos^{2} (x) d x

$\displaystyle\int {\sin}^{2}\left(x\right){\cos}^{2}\left(x\right)dx$

12. $\displaystyle\int {x}^{3}\sqrt{{x}^{2}+2}dx$

Show Solution

\frac{1}{15} {(x^{2} + 2)}^{\frac{3}{2}} (3 x^{2} - 4) + C

$\frac{1}{15}{\left({x}^{2}+2\right)}^{\frac{3}{2}}\left(3{x}^{2}-4\right)+C$

13.

\int \frac{3 x^{2} + 1}{x^{4} - 2 x^{3} - x^{2} + 2 x} d x

$\displaystyle\int \frac{3{x}^{2}+1}{{x}^{4}-2{x}^{3}-{x}^{2}+2x}dx$

14. $\displaystyle\int \frac{1}{{x}^{4}+4}dx$

Show Solution

\frac{1}{16} ln (\frac{x^{2} + 2 x + 2}{x^{2} - 2 x + 2}) - \frac{1}{8} \tan^{- 1} (1 - x) + \frac{1}{8} \tan^{- 1} (x + 1) + C

$\frac{1}{16}\text{ln}\left(\frac{{x}^{2}+2x+2}{{x}^{2}-2x+2}\right)-\frac{1}{8}{\tan}^{-1}\left(1-x\right)+\frac{1}{8}{\tan}^{-1}\left(x+1\right)+C$

15.

\int \frac{\sqrt{3 + 16 x^{4}}}{x^{4}} d x

$\displaystyle\int \frac{\sqrt{3+16{x}^{4}}}{{x}^{4}}dx$

For the following exercises, approximate the integrals using the midpoint rule, trapezoidal rule, and Simpson’s rule using four subintervals, rounding to three decimals.

16. [T] ${\displaystyle\int }_{1}^{2}\sqrt{{x}^{5}+2}dx$

Show Solution

M_{4} = 3.312, T_{4} = 3.354, S_{4} = 3.326

${\text{M}}_{4}=3.312,{\text{T}}_{4}=3.354,{S}_{4}=3.326$

17. [T]

\int_{0}^{\sqrt{π}} e^{- \sin (x^{2})} d x

${\displaystyle\int }_{0}^{\sqrt{\pi }}{e}^{\text{-}\sin\left({x}^{2}\right)}dx$

18. [T] ${\displaystyle\int }_{1}^{4}\frac{\text{ln}\frac{1}{x}}{x}dx$

Show Solution

M_{4} = - 0.982, T_{4} = - 0.917, S_{4} = - 0.952

${\text{M}}_{4}=-0.982,{\text{T}}_{4}=-0.917,{S}_{4}=-0.952$

For the following exercises, evaluate the integrals, if possible.

19.

\int_{1}^{\infty} \frac{1}{x^{n}} d x

${\displaystyle\int }_{1}^{\infty }\frac{1}{{x}^{n}}dx$ , for what values of

n

$n$ does this integral converge or diverge?

20. ${\displaystyle\int }_{1}^{\infty }\frac{{e}^{\text{-}x}}{x}dx$

Show Solution

For the following exercises, consider the gamma function given by $\Gamma\left(a\right)={\displaystyle\int }_{0}^{\infty }{e}^{\text{-}y}{y}^{a - 1}dy$ .

21. Show that

Γ (a) = (a - 1) Γ (a - 1)

$\Gamma\left(a\right)=\left(a - 1\right)\Gamma\left(a - 1\right)$ .

22. Extend to show that

Γ (a) = (a - 1)!

$\Gamma\left(a\right)=\left(a - 1\right)\text{!}$ , assuming

a

$a$ is a positive integer.

The fastest car in the world, the Bugati Veyron, can reach a top speed of 408 km/h. The graph represents its velocity.

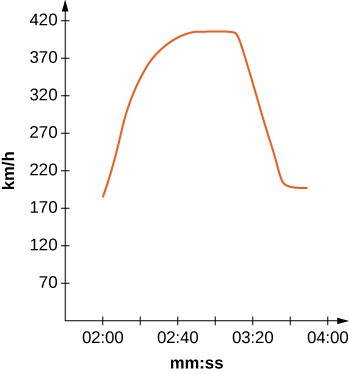
This figure has a graph in the first quadrant. It increases to where x is approximately 03:00 mm:ss and then drops off steep. The maximum height of the graph, here the drop occurs is approximately 420 km/h.

23. [T] Use the graph to estimate the velocity every 20 sec and fit to a graph of the form

v (t) = a {exp}^{b x} \sin (c x) + d

$v\left(t\right)=a{\text{exp}}^{bx}\sin\left(cx\right)+d$ . (Hint: Consider the time units.)

24. [T] Using your function from the previous problem, find exactly how far the Bugati Veyron traveled in the 1 min 40 sec included in the graph.

Show Solution

Answers may vary. Ex:

9.405

$9.405$ km

Techniques of Integration: Supplemental Content

Module 3 Review Problems

Candela Citations