Learning Outcomes
- Use the comparison theorem to determine whether a definite integral is convergent
It is not always easy or even possible to evaluate an improper integral directly; however, by comparing it with another carefully chosen integral, it may be possible to determine its convergence or divergence. To see this, consider two continuous functions [latex]f\left(x\right)[/latex] and [latex]g\left(x\right)[/latex] satisfying [latex]0\le f\left(x\right)\le g\left(x\right)[/latex] for [latex]x\ge a[/latex] (Figure 5). In this case, we may view integrals of these functions over intervals of the form [latex]\left[a,t\right][/latex] as areas, so we have the relationship
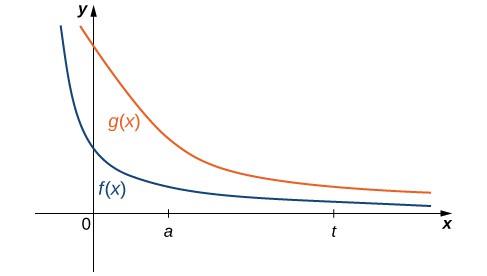
Figure 5. If [latex]0\le f\left(x\right)\le g\left(x\right)[/latex] for [latex]x\ge a[/latex], then for [latex]t\ge a[/latex], [latex]{\displaystyle\int }_{a}^{t}f\left(x\right)dx\le {\displaystyle\int }_{a}^{t}g\left(x\right)dx[/latex].
Thus, if
then
[latex]{\displaystyle\int }_{a}^{+\infty }g\left(x\right)dx=\underset{t\to \text{+}\infty }{\text{lim}}{\displaystyle\int }_{a}^{t}g\left(x\right)dx=\text{+}\infty[/latex] as well. That is, if the area of the region between the graph of [latex]f\left(x\right)[/latex] and the x-axis over [latex]\left[a,\text{+}\infty \right)[/latex] is infinite, then the area of the region between the graph of [latex]g\left(x\right)[/latex] and the x-axis over [latex]\left[a,\text{+}\infty \right)[/latex] is infinite too.
On the other hand, if
[latex]{\displaystyle\int }_{a}^{+\infty }g\left(x\right)dx=\underset{t\to \text{+}\infty }{\text{lim}}{\displaystyle\int }_{a}^{t}g\left(x\right)dx=L[/latex] for some real number [latex]L[/latex], then
[latex]{\displaystyle\int }_{a}^{+\infty }f\left(x\right)dx=\underset{t\to \text{+}\infty }{\text{lim}}{\displaystyle\int }_{a}^{t}f\left(x\right)dx[/latex] must converge to some value less than or equal to [latex]L[/latex], since [latex]{\displaystyle\int }_{a}^{t}f\left(x\right)dx[/latex] increases as [latex]t[/latex] increases and [latex]{\displaystyle\int }_{a}^{t}f\left(x\right)dx\le L[/latex] for all [latex]t\ge a[/latex].
If the area of the region between the graph of [latex]g\left(x\right)[/latex] and the x-axis over [latex]\left[a,\text{+}\infty \right)[/latex] is finite, then the area of the region between the graph of [latex]f\left(x\right)[/latex] and the x-axis over [latex]\left[a,\text{+}\infty \right)[/latex] is also finite.
These conclusions are summarized in the following theorem.
A Comparison Theorem
Let [latex]f\left(x\right)[/latex] and [latex]g\left(x\right)[/latex] be continuous over [latex]\left[a,\text{+}\infty \right)[/latex]. Assume that [latex]0\le f\left(x\right)\le g\left(x\right)[/latex] for [latex]x\ge a[/latex].
- If [latex]{\displaystyle\int }_{a}^{+\infty }f\left(x\right)dx=\underset{t\to \text{+}\infty }{\text{lim}}{\displaystyle\int }_{a}^{t}f\left(x\right)dx=\text{+}\infty[/latex], then [latex]{\displaystyle\int }_{a}^{+\infty }g\left(x\right)dx=\underset{t\to \text{+}\infty }{\text{lim}}{\displaystyle\int }_{a}^{t}g\left(x\right)dx=\text{+}\infty[/latex].
- If [latex]{\displaystyle\int }_{a}^{+\infty }g\left(x\right)dx=\underset{t\to \text{+}\infty }{\text{lim}}{\displaystyle\int }_{a}^{t}g\left(x\right)dx=L[/latex], where [latex]L[/latex] is a real number, then [latex]{\displaystyle\int }_{a}^{+\infty }f\left(x\right)dx=\underset{t\to \text{+}\infty }{\text{lim}}{\displaystyle\int }_{a}^{t}f\left(x\right)dx=M[/latex] for some real number [latex]M\le L[/latex].
Since utilizing this comparison theorem requires the use of inequalities, it is helpful to note the following fact when comparing functions.
Recall: Algebra of inequalities
If [latex]0 < f(x) \le g(x)[/latex], then [latex]\frac{1}{f(x)} \ge \frac{1}{g(x)}[/latex] In other words, a smaller denominator corresponds to a larger fraction, and vice versa.
Example: Applying the Comparison Theorem
Use a comparison to show that [latex]{\displaystyle\int }_{1}^{+\infty }\frac{1}{x{e}^{x}}dx[/latex] converges.
Example: Applying the Comparison Theorem
Use the comparison theorem to show that [latex]{\displaystyle\int }_{1}^{+\infty }\frac{1}{{x}^{p}}dx[/latex] diverges for all [latex]p<1[/latex].
try it
Use a comparison to show that [latex]{\displaystyle\int }_{e}^{+\infty }\frac{\text{ln}x}{x}dx[/latex] diverges.
Watch the following video to see the worked solution to the above Try It
For closed captioning, open the video on its original page by clicking the Youtube logo in the lower right-hand corner of the video display. In YouTube, the video will begin at the same starting point as this clip, but will continue playing until the very end.
You can view the transcript for this segmented clip of “3.7 Improper Integrals” here (opens in new window).
ACTIVITY: Laplace Transforms
In the last few modules, we have looked at several ways to use integration for solving real-world problems. For this next project, we are going to explore a more advanced application of integration: integral transforms. Specifically, we describe the Laplace transform and some of its properties. The Laplace transform is used in engineering and physics to simplify the computations needed to solve some problems. It takes functions expressed in terms of time and transforms them to functions expressed in terms of frequency. It turns out that, in many cases, the computations needed to solve problems in the frequency domain are much simpler than those required in the time domain.
The Laplace transform is defined in terms of an integral as
Note that the input to a Laplace transform is a function of time, [latex]f\left(t\right)[/latex], and the output is a function of frequency, [latex]F\left(s\right)[/latex]. Although many real-world examples require the use of complex numbers (involving the imaginary number [latex]i=\sqrt{-1}[/latex]), in this project we limit ourselves to functions of real numbers.
Let’s start with a simple example. Here we calculate the Laplace transform of [latex]f\left(t\right)=t[/latex] . We have
This is an improper integral, so we express it in terms of a limit, which gives
Now we use integration by parts to evaluate the integral. Note that we are integrating with respect to t, so we treat the variable s as a constant. We have
Then we obtain
- Calculate the Laplace transform of [latex]f\left(t\right)=1[/latex].
- Calculate the Laplace transform of [latex]f\left(t\right)={e}^{-3t}[/latex].
- Calculate the Laplace transform of [latex]f\left(t\right)={t}^{2}[/latex]. (Note, you will have to integrate by parts twice.)
Laplace transforms are often used to solve differential equations. Differential equations are not covered in detail until later in this book; but, for now, let’s look at the relationship between the Laplace transform of a function and the Laplace transform of its derivative.
Let’s start with the definition of the Laplace transform. We have
[latex]L\left\{f\left(t\right)\right\}={\displaystyle\int }_{0}^{\infty }{e}^{\text{-}st}f\left(t\right)dt=\underset{z\to \infty }{\text{lim}}{\displaystyle\int }_{0}^{z}{e}^{\text{-}st}f\left(t\right)dt[/latex]. - Use integration by parts to evaluate [latex]\underset{z\to \infty }{\text{lim}}{\displaystyle\int }_{0}^{z}{e}^{\text{-}st}f\left(t\right)dt[/latex]. (Let [latex]u=f\left(t\right)[/latex] and [latex]dv={e}^{\text{-}st}dt.[/latex])
After integrating by parts and evaluating the limit, you should see that
[latex]L\left\{f\left(t\right)\right\}=\frac{f\left(0\right)}{s}+\frac{1}{s}\left[L\left\{{f}^{\prime }\left(t\right)\right\}\right][/latex].
Then,
[latex]L\left\{{f}^{\prime }\left(t\right)\right\}=sL\left\{f\left(t\right)\right\}-f\left(0\right)[/latex].
Thus, differentiation in the time domain simplifies to multiplication by s in the frequency domain.
The final thing we look at in this project is how the Laplace transforms of [latex]f\left(t\right)[/latex] and its antiderivative are related. Let [latex]g\left(t\right)={\displaystyle\int }_{0}^{t}f\left(u\right)du[/latex]. Then,
[latex]L\left\{g\left(t\right)\right\}={\displaystyle\int }_{0}^{\infty }{e}^{\text{-}st}g\left(t\right)dt=\underset{z\to \infty }{\text{lim}}{\displaystyle\int }_{0}^{z}{e}^{\text{-}st}g\left(t\right)dt[/latex]. - Use integration by parts to evaluate [latex]\underset{z\to \infty }{\text{lim}}{\displaystyle\int }_{0}^{z}{e}^{\text{-}st}g\left(t\right)dt[/latex]. (Let [latex]u=g\left(t\right)[/latex] and [latex]dv={e}^{\text{-}st}dt[/latex]. Note, by the way, that we have defined [latex]g\left(t\right)[/latex], [latex]du=f\left(t\right)dt.[/latex]
As you might expect, you should see that
[latex]L\left\{g\left(t\right)\right\}=\frac{1}{s}\cdot L\left\{f\left(t\right)\right\}[/latex].
Integration in the time domain simplifies to division by s in the frequency domain.
Candela Citations
- 3.7 Improper Integrals. Authored by: Ryan Melton. License: CC BY: Attribution
- Calculus Volume 2. Authored by: Gilbert Strang, Edwin (Jed) Herman. Provided by: OpenStax. Located at: https://openstax.org/books/calculus-volume-2/pages/1-introduction. License: CC BY-NC-SA: Attribution-NonCommercial-ShareAlike. License Terms: Access for free at https://openstax.org/books/calculus-volume-2/pages/1-introduction
