Learning Outcomes
- Solve applied problems involving first-order linear differential equations
We look at two different applications of first-order linear differential equations. The first involves air resistance as it relates to objects that are rising or falling; the second involves an electrical circuit. Other applications are numerous, but most are solved in a similar fashion.
Free fall with air resistance
We discussed air resistance at the beginning of this section. The next example shows how to apply this concept for a ball in vertical motion. Other factors can affect the force of air resistance, such as the size and shape of the object, but we ignore them here.
Example: A Ball with Air Resistance
A racquetball is hit straight upward with an initial velocity of [latex]2[/latex] m/s. The mass of a racquetball is approximately [latex]0.0427[/latex] kg. Air resistance acts on the ball with a force numerically equal to [latex]0.5v[/latex], where [latex]v[/latex] represents the velocity of the ball at time [latex]t[/latex].
- Find the velocity of the ball as a function of time.
- How long does it take for the ball to reach its maximum height?
- If the ball is hit from an initial height of [latex]1[/latex] meter, how high will it reach?
Watch the following video to see the worked solution to Example: A Ball with Air Resistance.
For closed captioning, open the video on its original page by clicking the Youtube logo in the lower right-hand corner of the video display. In YouTube, the video will begin at the same starting point as this clip, but will continue playing until the very end.
You can view the transcript for this segmented clip of “4.5.3” here (opens in new window).
try it
The weight of a penny is [latex]2.5[/latex] grams (United States Mint, “Coin Specifications,” accessed April 9, 2015, http://www.usmint.gov/about_the_mint/?action=coin_specifications), and the upper observation deck of the Empire State Building is [latex]369[/latex] meters above the street. Since the penny is a small and relatively smooth object, air resistance acting on the penny is actually quite small. We assume the air resistance is numerically equal to [latex]0.0025v[/latex]. Furthermore, the penny is dropped with no initial velocity imparted to it.
- Set up an initial-value problem that represents the falling penny.
- Solve the problem for [latex]v\left(t\right)[/latex].
- What is the terminal velocity of the penny (i.e., calculate the limit of the velocity as [latex]t[/latex] approaches infinity)?
Electrical Circuits
A source of electromotive force (e.g., a battery or generator) produces a flow of current in a closed circuit, and this current produces a voltage drop across each resistor, inductor, and capacitor in the circuit. Kirchhoff’s Loop Rule states that the sum of the voltage drops across resistors, inductors, and capacitors is equal to the total electromotive force in a closed circuit. We have the following three results:
- The voltage drop across a resistor is given by
[latex]{E}_{R}=Ri[/latex],
where [latex]R[/latex] is a constant of proportionality called the resistance, and [latex]i[/latex] is the current. - The voltage drop across an inductor is given by
[latex]{E}_{L}=L{i}^{\prime }[/latex],
where [latex]L[/latex] is a constant of proportionality called the inductance, and [latex]i[/latex] again denotes the current. - The voltage drop across a capacitor is given by
[latex]{E}_{C}=\frac{1}{C}q[/latex],
where [latex]C[/latex] is a constant of proportionality called the capacitance, and [latex]q[/latex] is the instantaneous charge on the capacitor. The relationship between [latex]i[/latex] and [latex]q[/latex] is [latex]i={q}^{\prime }[/latex].
We use units of volts [latex]\left(\text{V}\right)[/latex] to measure voltage [latex]E[/latex], amperes [latex]\left(\text{A}\right)[/latex] to measure current [latex]i[/latex], coulombs [latex]\left(\text{C}\right)[/latex] to measure charge [latex]q[/latex], ohms [latex]\left(\Omega \right)[/latex] to measure resistance [latex]R[/latex], henrys [latex]\left(\text{H}\right)[/latex] to measure inductance [latex]L[/latex], and farads [latex]\left(\text{F}\right)[/latex] to measure capacitance [latex]C[/latex]. Consider the circuit in Figure 2.
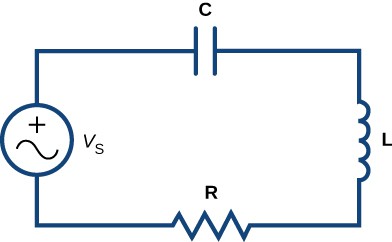
Figure 2. A typical electric circuit, containing a voltage generator [latex]\left({V}_{S}\right)[/latex], capacitor [latex]\left(C\right)[/latex], inductor [latex]\left(L\right)[/latex], and resistor [latex]\left(R\right)[/latex].
Applying Kirchhoff’s Loop Rule to this circuit, we let [latex]E[/latex] denote the electromotive force supplied by the voltage generator. Then
Substituting the expressions for [latex]{E}_{L},{E}_{R}[/latex], and [latex]{E}_{C}[/latex] into this equation, we obtain
If there is no capacitor in the circuit, then the equation becomes
This is a first-order differential equation in [latex]i[/latex]. The circuit is referred to as an [latex]LR[/latex] circuit.
Next, suppose there is no inductor in the circuit, but there is a capacitor and a resistor, so [latex]L=0,R\ne 0[/latex], and [latex]C\ne 0[/latex]. Then [latex]y=\dfrac{1}{\mu \left(x\right)}\left[\displaystyle\int \mu \left(x\right)q\left(x\right)dx+C\right][/latex] can be rewritten as
which is a first-order linear differential equation. This is referred to as an RC circuit. In either case, we can set up and solve an initial-value problem.
Example: Finding Current in an RL Electric Circuit
A circuit has in series an electromotive force given by [latex]E=50\sin{20t}\text{ V}[/latex], a resistor of [latex]5 \Omega[/latex], and an inductor of [latex]0.4\text{H}\text{.}[/latex] If the initial current is [latex]0[/latex], find the current at time [latex]t>0[/latex].
try it
A circuit has in series an electromotive force given by [latex]E=20\sin5t[/latex] V, a capacitor with capacitance [latex]0.02\text{F}[/latex], and a resistor of [latex]8 \Omega[/latex]. If the initial charge is [latex]4\text{C}[/latex], find the charge at time [latex]t>0[/latex].
![A graph of the given solution over [0, 6] on the x axis. It is an oscillating function, rapidly going from just below -5 to just above 5.](https://s3-us-west-2.amazonaws.com/courses-images/wp-content/uploads/sites/4175/2019/04/11234229/CNX_Calc_Figure_08_05_004.jpg)
