Learning Outcomes
- Describe the common applied conditions of a catenary curve
One physical application of hyperbolic functions involves hanging cables. If a cable of uniform density is suspended between two supports without any load other than its own weight, the cable forms a curve called a catenary. High-voltage power lines, chains hanging between two posts, and strands of a spider’s web all form catenaries. The following figure shows chains hanging from a row of posts.

Figure 3. Chains between these posts take the shape of a catenary. (credit: modification of work by OKFoundryCompany, Flickr)
Hyperbolic functions can be used to model catenaries. Specifically, functions of the form [latex]y=a\text{cosh}\left(\frac{x}{a}\right)[/latex] are catenaries. Figure 4 shows the graph of [latex]y=2\text{cosh}\left(\frac{x}{2}\right).[/latex]
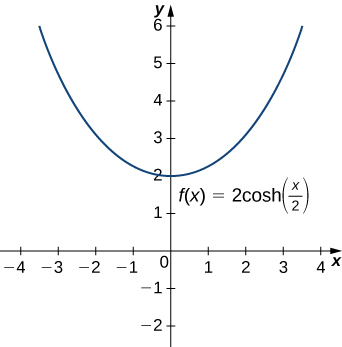
Figure 4. A hyperbolic cosine function forms the shape of a catenary.
example: Using a Catenary to Find the Length of a Cable
Assume a hanging cable has the shape [latex]10\text{cosh}\left(\frac{x}{10}\right)[/latex] for [latex]-15\le x\le 15,[/latex] where [latex]x[/latex] is measured in feet. Determine the length of the cable (in feet).
Watch the following video to see the worked solution to Example: Using a Catenary to Find the Length of a Cable.
Try It
Assume a hanging cable has the shape [latex]15\text{cosh}\left(\frac{x}{15}\right)[/latex] for [latex]-20\le x\le 20.[/latex] Determine the length of the cable (in feet).
Try It
Candela Citations
- 6.9.3 #73 (edited). Authored by: Ryan Melton. License: CC BY: Attribution
- Calculus Volume 2. Authored by: Gilbert Strang, Edwin (Jed) Herman. Provided by: OpenStax. Located at: https://openstax.org/books/calculus-volume-2/pages/1-introduction. License: CC BY-NC-SA: Attribution-NonCommercial-ShareAlike. License Terms: Access for free at https://openstax.org/books/calculus-volume-2/pages/1-introduction
