Area of a Region between Two Curves

Let [latex]f(x)[/latex] and [latex]g(x)[/latex] be continuous functions over an interval [latex]\left[a,b\right][/latex] such that [latex]f(x)\ge g(x)[/latex] on [latex]\left[a,b\right].[/latex] We want to find the area between the graphs of the functions, as shown in the following figure.

Figure 1. The area between the graphs of two functions, [latex]f(x)[/latex] and [latex]g(x),[/latex] on the interval [latex]\left[a,b\right].[/latex]

As we did before, we are going to partition the interval on the [latex]x\text{-axis}[/latex] and approximate the area between the graphs of the functions with rectangles. So, for [latex]i=0,1,2\text{,…},n,[/latex] let [latex]P=\left\{{x}_{i}\right\}[/latex] be a regular partition of [latex]\left[a,b\right].[/latex] Then, for [latex]i=1,2\text{,…},n,[/latex] choose a point [latex]{x}_{i}^{*}\in \left[{x}_{i-1},{x}_{i}\right],[/latex] and on each interval [latex]\left[{x}_{i-1},{x}_{i}\right][/latex] construct a rectangle that extends vertically from [latex]g({x}_{i}^{*})[/latex] to [latex]f({x}_{i}^{*}).[/latex] Figure 2(a) shows the rectangles when [latex]{x}_{i}^{*}[/latex] is selected to be the left endpoint of the interval and [latex]n=10.[/latex] Figure 2(b) shows a representative rectangle in detail.

Figure 2. (a)We can approximate the area between the graphs of two functions, [latex]f(x)[/latex] and [latex]g(x),[/latex] with rectangles. (b) The area of a typical rectangle goes from one curve to the other.

The height of each individual rectangle is [latex]f({x}_{i}^{*})-g({x}_{i}^{*})[/latex] and the width of each rectangle is [latex]\text{Δ}x.[/latex] Adding the areas of all the rectangles, we see that the area between the curves is approximated by

This is a Riemann sum, so we take the limit as [latex]n\to \infty [/latex] and we get

These findings are summarized in the following theorem.

We apply this theorem in the following example.

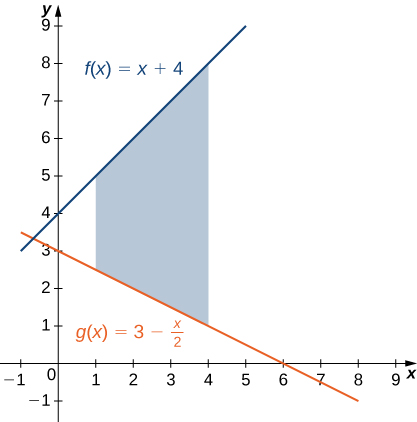
Example: Finding the Area of a Region between Two Curves 1

If R is the region bounded above by the graph of the function [latex]f(x)=x+4[/latex] and below by the graph of the function [latex]g(x)=3-\frac{x}{2}[/latex] over the interval [latex]\left[1,4\right],[/latex] find the area of region [latex]R.[/latex]

Show Solution

The region is depicted in the following figure.

Figure 3. A region between two curves is shown where one curve is always greater than the other.

We have

[latex]\begin{array}{cc}\hfill A& ={\displaystyle\int }_{a}^{b}\left[f(x)-g(x)\right]dx\hfill \\ & ={\displaystyle\int }_{1}^{4}\left[(x+4)-(3-\frac{x}{2})\right]dx={\displaystyle\int }_{1}^{4}\left[\frac{3x}{2}+1\right]dx\hfill \\ & ={\left[\frac{3{x}^{2}}{4}+x\right]|}_{1}^{4}=(16-\frac{7}{4})=\frac{57}{4}.\hfill \end{array}[/latex]

The area of the region is [latex]\frac{57}{4}{\text{units}}^{2}.[/latex]

In the last example, we defined the interval of interest as part of the problem statement. Quite often, though, we want to define our interval of interest based on where the graphs of the two functions intersect. This is illustrated in the following example.

Example: Finding the Area of a Region between Two Curves 2

If [latex]R[/latex] is the region bounded above by the graph of the function [latex]f(x)=9-{(\frac{x}{2})}^{2}[/latex] and below by the graph of the function [latex]g(x)=6-x,[/latex] find the area of region [latex]R.[/latex]

Show Solution

The region is depicted in the following figure.

Figure 4. This graph shows the region below the graph of [latex]f(x)[/latex] and above the graph of [latex]g(x).[/latex]

We first need to compute where the graphs of the functions intersect. Setting [latex]f(x)=g(x),[/latex] we get

[latex]\begin{array}{ccc}\hfill f(x)& =\hfill & g(x)\hfill \\ \\ \hfill 9-{(\frac{x}{2})}^{2}& =\hfill & 6-x\hfill \\ \hfill 9-\frac{{x}^{2}}{4}& =\hfill & 6-x\hfill \\ \hfill 36-{x}^{2}& =\hfill & 24-4x\hfill \\ \hfill {x}^{2}-4x-12& =\hfill & 0\hfill \\ \hfill (x-6)(x+2)& =\hfill & 0.\hfill \end{array}[/latex]

The graphs of the functions intersect when [latex]x=6[/latex] or [latex]x=-2,[/latex] so we want to integrate from -2 to 6. Since [latex]f(x)\ge g(x)[/latex] for [latex]-2\le x\le 6,[/latex] we obtain

[latex]\begin{array}{cc}\hfill A& ={\displaystyle\int }_{a}^{b}\left[f(x)-g(x)\right]dx\hfill \\ & ={\displaystyle\int }_{-2}^{6}\left[9-{(\frac{x}{2})}^{2}-(6-x)\right]dx={\displaystyle\int }_{-2}^{6}\left[3-\frac{{x}^{2}}{4}+x\right]dx\hfill \\ & ={\left[3x-\frac{{x}^{3}}{12}+\frac{{x}^{2}}{2}\right]|}_{-2}^{6}=\frac{64}{3}.\hfill \end{array}[/latex]

The area of the region is [latex]\frac{64}{3}[/latex] units².

Watch the following video to see the worked solution to the above Try It.

Areas of Compound Regions

So far, we have required [latex]f(x)\ge g(x)[/latex] over the entire interval of interest, but what if we want to look at regions bounded by the graphs of functions that cross one another? In that case, we modify the process we just developed by using the absolute value function.

In practice, applying this theorem requires us to break up the interval [latex]\left[a,b\right][/latex] and evaluate several integrals, depending on which of the function values is greater over a given part of the interval. We study this process in the following example.

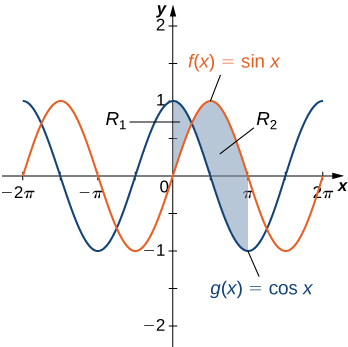
Example: Finding the Area of a Region Bounded by Functions That Cross

If R is the region between the graphs of the functions [latex]f(x)= \sin x[/latex] and [latex]g(x)= \cos x[/latex] over the interval [latex]\left[0,\pi \right],[/latex] find the area of region [latex]R.[/latex]

Show Solution

The region is depicted in the following figure.

Figure 5. The region between two curves can be broken into two sub-regions.

The graphs of the functions intersect at [latex]x=\pi \text{/}4.[/latex] For [latex]x\in \left[0,\pi \text{/}4\right],[/latex] [latex] \cos x\ge \sin x,[/latex] so

[latex]|f(x)-g(x)|=| \sin x- \cos x|= \cos x- \sin x[/latex]

On the other hand, for [latex]x\in \left[\pi \text{/}4,\pi \right],[/latex] [latex] \sin x\ge \cos x,[/latex] so

[latex]|f(x)-g(x)|=| \sin x- \cos x|= \sin x- \cos x[/latex]

Then

[latex]\begin{array}{cc}\hfill A& ={\displaystyle\int }_{a}^{b}|f(x)-g(x)|dx\hfill \\ & ={\displaystyle\int }_{0}^{\pi }| \sin x- \cos x|dx={\displaystyle\int }_{0}^{\pi \text{/}4}( \cos x- \sin x)dx+{\displaystyle\int }_{\pi \text{/}4}^{\pi }( \sin x- \cos x)dx\hfill \\ & ={\left[ \sin x+ \cos x\right]|}_{0}^{\pi \text{/}4}+{\left[\text{−} \cos x- \sin x\right]|}_{\pi \text{/}4}^{\pi }\hfill \\ & =(\sqrt{2}-1)+(1+\sqrt{2})=2\sqrt{2}.\hfill \end{array}[/latex]

The area of the region is [latex]2\sqrt{2}[/latex] units².

Watch the following video to see the worked solution to the above Try It.

Example: Finding the Area of a Complex Region

Consider the region depicted in Figure 6. Find the area of [latex]R.[/latex]

Figure 6. Two integrals are required to calculate the area of this region.

Show Solution

As with the last example, we need to divide the interval into two pieces. The graphs of the functions intersect at [latex]x=1[/latex] (set [latex]f(x)=g(x)[/latex] and solve for [latex]x[/latex]), so we evaluate two separate integrals: one over the interval [latex]\left[0,1\right][/latex] and one over the interval [latex]\left[1,2\right].[/latex]

Over the interval [latex]\left[0,1\right],[/latex] the region is bounded above by [latex]f(x)={x}^{2}[/latex] and below by the [latex]x[/latex]-axis, so we have

[latex]{A}_{1}={\displaystyle\int }_{0}^{1}{x}^{2}dx={\frac{{x}^{3}}{3}|}_{0}^{1}=\frac{1}{3}.[/latex]

Over the interval [latex]\left[1,2\right],[/latex] the region is bounded above by [latex]g(x)=2-x[/latex] and below by the [latex]x\text{-axis,}[/latex] so we have

[latex]{A}_{2}={\displaystyle\int }_{1}^{2}(2-x)dx={\left[2x-\frac{{x}^{2}}{2}\right]|}_{1}^{2}=\frac{1}{2}.[/latex]

Adding these areas together, we obtain

[latex]A={A}_{1}+{A}_{2}=\frac{1}{3}+\frac{1}{2}=\frac{5}{6}.[/latex]

The area of the region is [latex]\frac{5}{6}[/latex] units².

Try It

Consider the region depicted in the following figure. Find the area of [latex]R.[/latex]

Figure 7.

Hint

The two curves intersect at [latex]x=1.[/latex]

Show Solution

[latex]\frac{5}{3}[/latex] units²

Watch the following video to see the worked solution to the above Try It.