For the following exercises, determine whether the statement is true or false. Justify your answer with a proof or a counterexample.
1. [latex]\displaystyle\int {e}^{x}\sin\left(x\right)dx[/latex] cannot be integrated by parts.
2. [latex]\displaystyle\int \frac{1}{{x}^{4}+1}dx[/latex] cannot be integrated using partial fractions.
3. In numerical integration, increasing the number of points decreases the error.
4. Integration by parts can always yield the integral.
For the following exercises, evaluate the integral using the specified method.
5. [latex]\displaystyle\int {x}^{2}\sin\left(4x\right)dx[/latex] using integration by parts
6. [latex]\displaystyle\int \frac{1}{{x}^{2}\sqrt{{x}^{2}+16}}dx[/latex] using trigonometric substitution
Show Solution
[latex]-\frac{\sqrt{{x}^{2}+16}}{16x}+C[/latex]
7. [latex]\displaystyle\int \sqrt{x}\text{ln}\left(x\right)dx[/latex] using integration by parts
8. [latex]\displaystyle\int \frac{3x}{{x}^{3}+2{x}^{2}-5x - 6}dx[/latex] using partial fractions
Show Solution
[latex]\frac{1}{10}\left(4\text{ln}\left(2-x\right)+5\text{ln}\left(x+1\right)-9\text{ln}\left(x+3\right)\right)+C[/latex]
9. [latex]\displaystyle\int \frac{{x}^{5}}{{\left(4{x}^{2}+4\right)}^{\frac{5}{2}}}dx[/latex] using trigonometric substitution
10. [latex]\displaystyle\int \frac{\sqrt{4-{\sin}^{2}\left(x\right)}}{{\sin}^{2}\left(x\right)}\cos\left(x\right)dx[/latex] using a table of integrals or a CAS
Show Solution
[latex]-\frac{\sqrt{4-{\sin}^{2}\left(x\right)}}{\sin\left(x\right)}-\frac{x}{2}+C[/latex]
For the following exercises, integrate using whatever method you choose.
11. [latex]\displaystyle\int {\sin}^{2}\left(x\right){\cos}^{2}\left(x\right)dx[/latex]
12. [latex]\displaystyle\int {x}^{3}\sqrt{{x}^{2}+2}dx[/latex]
Show Solution
[latex]\frac{1}{15}{\left({x}^{2}+2\right)}^{\frac{3}{2}}\left(3{x}^{2}-4\right)+C[/latex]
13. [latex]\displaystyle\int \frac{3{x}^{2}+1}{{x}^{4}-2{x}^{3}-{x}^{2}+2x}dx[/latex]
14. [latex]\displaystyle\int \frac{1}{{x}^{4}+4}dx[/latex]
Show Solution
[latex]\frac{1}{16}\text{ln}\left(\frac{{x}^{2}+2x+2}{{x}^{2}-2x+2}\right)-\frac{1}{8}{\tan}^{-1}\left(1-x\right)+\frac{1}{8}{\tan}^{-1}\left(x+1\right)+C[/latex]
15. [latex]\displaystyle\int \frac{\sqrt{3+16{x}^{4}}}{{x}^{4}}dx[/latex]
For the following exercises, approximate the integrals using the midpoint rule, trapezoidal rule, and Simpson’s rule using four subintervals, rounding to three decimals.
16. [T] [latex]{\displaystyle\int }_{1}^{2}\sqrt{{x}^{5}+2}dx[/latex]
Show Solution
[latex]{\text{M}}_{4}=3.312,{\text{T}}_{4}=3.354,{S}_{4}=3.326[/latex]
17. [T] [latex]{\displaystyle\int }_{0}^{\sqrt{\pi }}{e}^{\text{-}\sin\left({x}^{2}\right)}dx[/latex]
18. [T] [latex]{\displaystyle\int }_{1}^{4}\frac{\text{ln}\frac{1}{x}}{x}dx[/latex]
Show Solution
[latex]{\text{M}}_{4}=-0.982,{\text{T}}_{4}=-0.917,{S}_{4}=-0.952[/latex]
For the following exercises, evaluate the integrals, if possible.
19. [latex]{\displaystyle\int }_{1}^{\infty }\frac{1}{{x}^{n}}dx[/latex], for what values of [latex]n[/latex] does this integral converge or diverge?
20. [latex]{\displaystyle\int }_{1}^{\infty }\frac{{e}^{\text{-}x}}{x}dx[/latex]
Show Solution
approximately 0.2194
For the following exercises, consider the gamma function given by [latex]\Gamma\left(a\right)={\displaystyle\int }_{0}^{\infty }{e}^{\text{-}y}{y}^{a - 1}dy[/latex].
21. Show that [latex]\Gamma\left(a\right)=\left(a - 1\right)\Gamma\left(a - 1\right)[/latex].
22. Extend to show that [latex]\Gamma\left(a\right)=\left(a - 1\right)\text{!}[/latex], assuming [latex]a[/latex] is a positive integer.
The fastest car in the world, the Bugati Veyron, can reach a top speed of 408 km/h. The graph represents its velocity.
23. [T] Use the graph to estimate the velocity every 20 sec and fit to a graph of the form [latex]v\left(t\right)=a{\text{exp}}^{bx}\sin\left(cx\right)+d[/latex]. (Hint: Consider the time units.)
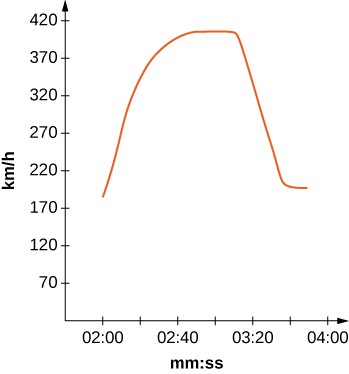
24. [T] Using your function from the previous problem, find exactly how far the Bugati Veyron traveled in the 1 min 40 sec included in the graph.
Show Solution
Answers may vary. Ex: [latex]9.405[/latex] km
