Problem Set: Partial Fractions

Express the rational function as a sum or difference of two simpler rational expressions.

\frac{1}{(x - 3) (x - 2)}

$\frac{1}{\left(x - 3\right)\left(x - 2\right)}$

2. $\frac{{x}^{2}+1}{x\left(x+1\right)\left(x+2\right)}$

Show Solution

- \frac{2}{x + 1} + \frac{5}{2 (x + 2)} + \frac{1}{2 x}

$-\frac{2}{x+1}+\frac{5}{2\left(x+2\right)}+\frac{1}{2x}$

\frac{1}{x^{3} - x}

$\frac{1}{{x}^{3}-x}$

4. $\frac{3x+1}{{x}^{2}}$

Show Solution

\frac{1}{x^{2}} + \frac{3}{x}

$\frac{1}{{x}^{2}}+\frac{3}{x}$

\frac{3 x^{2}}{x^{2} + 1}

$\frac{3{x}^{2}}{{x}^{2}+1}$ (Hint: Use long division first.)

6. $\frac{2{x}^{4}}{{x}^{2}-2x}$

Show Solution

2 x^{2} + 4 x + 8 + \frac{16}{x - 2}

$2{x}^{2}+4x+8+\frac{16}{x - 2}$

\frac{1}{(x - 1) (x^{2} + 1)}

$\frac{1}{\left(x - 1\right)\left({x}^{2}+1\right)}$

8. $\frac{1}{{x}^{2}\left(x - 1\right)}$

Show Solution

- \frac{1}{x^{2}} - \frac{1}{x} + \frac{1}{x - 1}

$-\frac{1}{{x}^{2}}-\frac{1}{x}+\frac{1}{x - 1}$

\frac{x}{x^{2} - 4}

$\frac{x}{{x}^{2}-4}$

10. $\frac{1}{x\left(x - 1\right)\left(x - 2\right)\left(x - 3\right)}$

Show Solution

- \frac{1}{2 (x - 2)} + \frac{1}{2 (x - 1)} - \frac{1}{6 x} + \frac{1}{6 (x - 3)}

$-\frac{1}{2\left(x - 2\right)}+\frac{1}{2\left(x - 1\right)}-\frac{1}{6x}+\frac{1}{6\left(x - 3\right)}$

11.

\frac{1}{x^{4} - 1} = \frac{1}{(x + 1) (x - 1) (x^{2} + 1)}

$\frac{1}{{x}^{4}-1}=\frac{1}{\left(x+1\right)\left(x - 1\right)\left({x}^{2}+1\right)}$

12. $\frac{3{x}^{2}}{{x}^{3}-1}=\frac{3{x}^{2}}{\left(x - 1\right)\left({x}^{2}+x+1\right)}$

Show Solution

\frac{1}{x - 1} + \frac{2 x + 1}{x^{2} + x + 1}

$\frac{1}{x - 1}+\frac{2x+1}{{x}^{2}+x+1}$

13.

\frac{2 x}{{(x + 2)}^{2}}

$\frac{2x}{{\left(x+2\right)}^{2}}$

14. $\frac{3{x}^{4}+{x}^{3}+20{x}^{2}+3x+31}{\left(x+1\right){\left({x}^{2}+4\right)}^{2}}$

Show Solution

\frac{2}{x + 1} + \frac{x}{x^{2} + 4} - \frac{1}{{(x^{2} + 4)}^{2}}

$\frac{2}{x+1}+\frac{x}{{x}^{2}+4}-\frac{1}{{\left({x}^{2}+4\right)}^{2}}$

Use the method of partial fractions to evaluate each of the following integrals.

15. $\displaystyle\int \frac{dx}{\left(x - 3\right)\left(x - 2\right)}$

16. $\displaystyle\int \frac{3x}{{x}^{2}+2x - 8}dx$

Show Solution

- ln | 2 - x | + 2 ln | 4 + x | + C

$\text{-}\text{ln}|2-x|+2\text{ln}|4+x|+C$

17.

\int \frac{d x}{x^{3} - x}

$\displaystyle\int \frac{dx}{{x}^{3}-x}$

18. $\displaystyle\int \frac{x}{{x}^{2}-4}dx$

Show Solution

\frac{1}{2} ln | 4 - x^{2} | + C

$\frac{1}{2}\text{ln}|4-{x}^{2}|+C$

19.

\int \frac{d x}{x (x - 1) (x - 2) (x - 3)}

$\displaystyle\int \frac{dx}{x\left(x - 1\right)\left(x - 2\right)\left(x - 3\right)}$

20. $\displaystyle\int \frac{2{x}^{2}+4x+22}{{x}^{2}+2x+10}dx$

Show Solution

2 (x + \frac{1}{3} arctan (\frac{1 + x}{3})) + C

$2\left(x+\frac{1}{3}\text{arctan}\left(\frac{1+x}{3}\right)\right)+C$

21.

\int \frac{d x}{x^{2} - 5 x + 6}

$\displaystyle\int \frac{dx}{{x}^{2}-5x+6}$

22. $\displaystyle\int \frac{2-x}{{x}^{2}+x}dx$

Show Solution

2 ln | x | - 3 ln | 1 + x | + C

$2\text{ln}|x|-3\text{ln}|1+x|+C$

23.

\int \frac{2}{x^{2} - x - 6} d x

$\displaystyle\int \frac{2}{{x}^{2}-x - 6}dx$

24. $\displaystyle\int \frac{dx}{{x}^{3}-2{x}^{2}-4x+8}$

Show Solution

\frac{1}{16} (- \frac{4}{- 2 + x} - ln | - 2 + x | + ln | 2 + x |) + C

$\frac{1}{16}\left(\text{-}\frac{4}{-2+x}-\text{ln}|-2+x|+\text{ln}|2+x|\right)+C$

25. $\displaystyle\int \frac{dx}{{x}^{4}-10{x}^{2}+9}$

Evaluate the following integrals, which have irreducible quadratic factors.

26. $\displaystyle\int \frac{2}{\left(x - 4\right)\left({x}^{2}+2x+6\right)}dx$

Show Solution

\frac{1}{30} (- 2 \sqrt{5} arctan [\frac{1 + x}{\sqrt{5}}] + 2 ln | - 4 + x | - ln | 6 + 2 x + x^{2} |) + C

$\frac{1}{30}\left(-2\sqrt{5}\text{arctan}\left[\frac{1+x}{\sqrt{5}}\right]+2\text{ln}|-4+x|-\text{ln}|6+2x+{x}^{2}|\right)+C$

27.

\int \frac{x^{2}}{x^{3} - x^{2} + 4 x - 4} d x

$\displaystyle\int \frac{{x}^{2}}{{x}^{3}-{x}^{2}+4x - 4}dx$

28. $\displaystyle\int \frac{{x}^{3}+6{x}^{2}+3x+6}{{x}^{3}+2{x}^{2}}dx$

Show Solution

- \frac{3}{x} + 4 ln | x + 2 | + x + C

$-\frac{3}{x}+4\text{ln}|x+2|+x+C$

29.

\int \frac{x}{(x - 1) {(x^{2} + 2 x + 2)}^{2}} d x

$\displaystyle\int \frac{x}{\left(x - 1\right){\left({x}^{2}+2x+2\right)}^{2}}dx$

Use the method of partial fractions to evaluate the following integrals.

30. $\displaystyle\int \frac{3x+4}{\left({x}^{2}+4\right)\left(3-x\right)}dx$

Show Solution

- ln | 3 - x | + \frac{1}{2} ln | x^{2} + 4 | + C

$\text{-}\text{ln}|3-x|+\frac{1}{2}\text{ln}|{x}^{2}+4|+C$

31.

\int \frac{2}{{(x + 2)}^{2} (2 - x)} d x

$\displaystyle\int \frac{2}{{\left(x+2\right)}^{2}\left(2-x\right)}dx$

32. $\displaystyle\int \frac{3x+4}{{x}^{3}-2x - 4}dx$ (Hint: Use the rational root theorem.)

Show Solution

ln | x - 2 | - \frac{1}{2} ln | x^{2} + 2 x + 2 | + C

$\text{ln}|x - 2|-\frac{1}{2}\text{ln}|{x}^{2}+2x+2|+C$

Use substitution to convert the integrals to integrals of rational functions. Then use partial fractions to evaluate the integrals.

33.

\int_{0}^{1} \frac{e^{x}}{36 - e^{2 x}} d x

${\displaystyle\int }_{0}^{1}\frac{{e}^{x}}{36-{e}^{2x}}dx$ (Give the exact answer and the decimal equivalent. Round to five decimal places.)

34. $\displaystyle\int \frac{{e}^{x}dx}{{e}^{2x}-{e}^{x}}dx$

Show Solution

- x + ln | 1 - e^{x} | + C

$\text{-}x+\text{ln}|1-{e}^{x}|+C$

35.

\int \frac{sin x d x}{1 - {cos}^{2} x}

$\displaystyle\int \frac{\sin{x}dx}{1-{\cos}^{2}x}$

36. $\displaystyle\int \frac{\sin{x}}{{\cos}^{2}x+\cos{x} - 6}dx$

Show Solution

\frac{1}{5} ln | \frac{cos x + 3}{cos x - 2} | + C

$\frac{1}{5}\text{ln}|\frac{\cos{x}+3}{\cos{x} - 2}|+C$

37.

\int \frac{1 - \sqrt{x}}{1 + \sqrt{x}} d x

$\displaystyle\int \frac{1-\sqrt{x}}{1+\sqrt{x}}dx$

38. $\displaystyle\int \frac{dt}{{\left({e}^{t}-{e}^{\text{-}t}\right)}^{2}}$

Show Solution

\frac{1}{2 - 2 e^{2 t}} + C

$\frac{1}{2 - 2{e}^{2t}}+C$

39.

\int \frac{1 + e^{x}}{1 - e^{x}} d x

$\displaystyle\int \frac{1+{e}^{x}}{1-{e}^{x}}dx$

40. $\displaystyle\int \frac{dx}{1+\sqrt{x+1}}$

Show Solution

2 \sqrt{1 + x} - 2 ln | 1 + \sqrt{1 + x} | + C

$2\sqrt{1+x}-2\text{ln}|1+\sqrt{1+x}|+C$

41.

\int \frac{d x}{\sqrt{x} + \sqrt[4]{x}}

$\displaystyle\int \frac{dx}{\sqrt{x}+\sqrt[4]{x}}$

42. $\displaystyle\int \frac{\cos{x}}{\sin{x}\left(1-\sin{x}\right)}dx$

Show Solution

ln | \frac{sin x}{1 - sin x} | + C

$\text{ln}|\frac{\sin{x}}{1-\sin{x}}|+C$

43.

\int \frac{e^{x}}{{(e^{2 x} - 4)}^{2}} d x

$\displaystyle\int \frac{{e}^{x}}{{\left({e}^{2x}-4\right)}^{2}}dx$

44. $\underset{1}{\overset{2}{\displaystyle\int }}\frac{1}{{x}^{2}\sqrt{4-{x}^{2}}}dx$

Show Solution

\frac{\sqrt{3}}{4}

$\frac{\sqrt{3}}{4}$

45.

\int \frac{1}{2 + e^{- x}} d x

$\displaystyle\int \frac{1}{2+{e}^{\text{-}x}}dx$

46. $\displaystyle\int \frac{1}{1+{e}^{x}}dx$

Show Solution

x - ln (1 + e^{x}) + C

$x-\text{ln}\left(1+{e}^{x}\right)+C$

Use the given substitution to convert the integral to an integral of a rational function, then evaluate.

47.

\int \frac{1}{t - \sqrt[3]{t}} d t t = x^{3}

$\displaystyle\int \frac{1}{t-\sqrt[3]{t}}dtt={x}^{3}$

48. $\displaystyle\int \frac{1}{\sqrt{x}+\sqrt[3]{x}}dx;x={u}^{6}$

Show Solution

6 x^{\frac{1}{6}} - 3 x^{\frac{1}{3}} + 2 \sqrt{x} - 6 ln (1 + x^{\frac{1}{6}}) + C

$6{x}^{\frac{1}{6}}-3{x}^{\frac{1}{3}}+2\sqrt{x}-6\text{ln}\left(1+{x}^{\frac{1}{6}}\right)+C$

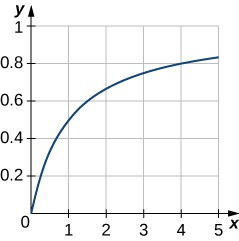
49. Graph the curve $y=\frac{x}{1+x}$ over the interval $\left[0,5\right]$ . Then, find the area of the region bounded by the curve, the x-axis, and the line $x=4$ .

This figure is a graph of the function y = x/(1 + x). The graph is only in the first quadrant. It begins at the origin and increases into the first quadrant. The curve stops at x = 5.

50. Find the volume of the solid generated when the region bounded by $y=\frac{1}{\sqrt{x\left(3-x\right)}}$ , $y=0$ , $x=1$ , and $x=2$ is revolved about the x-axis.

Show Solution

\frac{4}{3} π arctanh [\frac{1}{3}] = \frac{1}{3} π ln 4

$\frac{4}{3}\pi \text{arctanh}\left[\frac{1}{3}\right]=\frac{1}{3}\pi \text{ln}4$

51. The velocity of a particle moving along a line is a function of time given by

v (t) = \frac{88 t^{2}}{t^{2} + 1}

$v\left(t\right)=\frac{88{t}^{2}}{{t}^{2}+1}$ . Find the distance that the particle has traveled after

t = 5

$t=5$ sec.

Solve the initial-value problem for x as a function of t.

52. $\left({t}^{2}-7t+12\right)\frac{dx}{dt}=1,\left(t>4,x\left(5\right)=0\right)$

Show Solution

x = - ln | t - 3 | + ln | t - 4 | + ln 2

$x=\text{-}\text{ln}|t - 3|+\text{ln}|t - 4|+\text{ln}2$

53.

(t + 5) \frac{d x}{d t} = x^{2} + 1, t > - 5, x (1) = tan 1

$\left(t+5\right)\frac{dx}{dt}={x}^{2}+1,t>\text{-}5,x\left(1\right)=\tan1$

54. $\left(2{t}^{3}-2{t}^{2}+t - 1\right)\frac{dx}{dt}=3,x\left(2\right)=0$

Show Solution

x = ln | t - 1 | - \sqrt{2} arctan (\sqrt{2} t) - \frac{1}{2} ln (t^{2} + \frac{1}{2}) + \sqrt{2} arctan (2 \sqrt{2}) + \frac{1}{2} ln 4.5

$x=\text{ln}|t - 1|-\sqrt{2}\text{arctan}\left(\sqrt{2}t\right)-\frac{1}{2}\text{ln}\left({t}^{2}+\frac{1}{2}\right)+\sqrt{2}\text{arctan}\left(2\sqrt{2}\right)+\frac{1}{2}\text{ln}4.5$

55. Find the x-coordinate of the centroid of the area bounded by

y (x^{2} - 9) = 1

$y\left({x}^{2}-9\right)=1$ ,

y = 0, x = 4, and x = 5

$y=0,x=4,\text{and }x=5$ . (Round the answer to two decimal places.)

56. Find the volume generated by revolving the area bounded by $y=\frac{1}{{x}^{3}+7{x}^{2}+6x}x=1,x=7,\text{and }y=0$ about the y-axis.

Show Solution

\frac{2}{5} π ln \frac{28}{13}

$\frac{2}{5}\pi \text{ln}\frac{28}{13}$

57. Find the area bounded by

y = \frac{x - 12}{x^{2} - 8 x - 20}

$y=\frac{x - 12}{{x}^{2}-8x - 20}$ ,

y = 0, x = 2, and x = 4

$y=0,x=2,\text{and }x=4$ . (Round the answer to the nearest hundredth.)

58. Evaluate the integral $\displaystyle\int \frac{dx}{{x}^{3}+1}$ .

Show Solution

\frac{arctan [\frac{- 1 + 2 x}{\sqrt{3}}]}{\sqrt{3}} + \frac{1}{3} ln | 1 + x | - \frac{1}{6} ln | 1 - x + x^{2} | + C

$\frac{\text{arctan}\left[\frac{-1+2x}{\sqrt{3}}\right]}{\sqrt{3}}+\frac{1}{3}\text{ln}|1+x|-\frac{1}{6}\text{ln}|1-x+{x}^{2}|+C$

For the following problems, use the substitutions $\tan\left(\frac{x}{2}\right)=t$ , $dx=\frac{2}{1+{t}^{2}}dt$ , $\sin{x}=\frac{2t}{1+{t}^{2}}$ , and $\cos{x}=\frac{1-{t}^{2}}{1+{t}^{2}}$ .

59.

\int \frac{d x}{3 - 5 sin x}

$\displaystyle\int \frac{dx}{3 - 5\sin{x}}$

60. Find the area under the curve $y=\frac{1}{1+\sin{x}}$ between $x=0$ and $x=\pi$ . (Assume the dimensions are in inches.)

Show Solution

61. Given

tan (\frac{x}{2}) = t

$\tan\left(\frac{x}{2}\right)=t$ , derive the formulas

d x = \frac{2}{1 + t^{2}} d t

$dx=\frac{2}{1+{t}^{2}}dt$ ,

sin x = \frac{2 t}{1 + t^{2}}

$\sin{x}=\frac{2t}{1+{t}^{2}}$ , and

cos x = \frac{1 - t^{2}}{1 + t^{2}}

$\cos{x}=\frac{1-{t}^{2}}{1+{t}^{2}}$ .

62. Evaluate $\displaystyle\int \frac{\sqrt[3]{x - 8}}{x}dx$ .

Show Solution

3 {(- 8 + x)}^{\frac{1}{3}}

$3{\left(-8+x\right)}^{\frac{1}{3}}$

- 2 \sqrt{3} arctan [\frac{- 1 + {(- 8 + x)}^{\frac{1}{3}}}{\sqrt{3}}]

$-2\sqrt{3}\text{arctan}\left[\frac{-1+{\left(-8+x\right)}^{\frac{1}{3}}}{\sqrt{3}}\right]$

- 2 ln [2 + {(- 8 + x)}^{\frac{1}{3}}]

$-2\text{ln}\left[2+{\left(-8+x\right)}^{\frac{1}{3}}\right]$

+ ln [4 - 2 {(- 8 + x)}^{\frac{1}{3}} + {(- 8 + x)}^{\frac{2}{3}}] + C

$+\text{ln}\left[4 - 2{\left(-8+x\right)}^{\frac{1}{3}}+{\left(-8+x\right)}^{\frac{2}{3}}\right]+C$

Techniques of Integration: Supplemental Content

Problem Set: Partial Fractions

Candela Citations