Problem Set: Determining Volumes by Slicing

1. Derive the formula for the volume of a sphere using the slicing method.

2. Use the slicing method to derive the formula for the volume of a cone.

3. Use the slicing method to derive the formula for the volume of a tetrahedron with side length $a.$

4. Use the disk method to derive the formula for the volume of a trapezoidal cylinder.

5. Explain when you would use the disk method versus the washer method. When are they interchangeable?

For the following exercises (6-10), draw a typical slice and find the volume using the slicing method for the given volume.

6. A pyramid with height 6 units and square base of side 2 units, as pictured here.

This figure is a pyramid with base width of 2 and height of 6 units.

Show Solution

7. A pyramid with height 4 units and a rectangular base with length 2 units and width 3 units, as pictured here.

This figure is a pyramid with base width of 2, length of 3, and height of 4 units.

8. A tetrahedron with a base side of 4 units, as seen here.

This figure is an equilateral triangle with side length of 4 units.

Show Solution

$\frac{32}{3\sqrt{2}}$ units3

9. A pyramid with height 5 units, and an isosceles triangular base with lengths of 6 units and 8 units, as seen here.

This figure is a pyramid with a triangular base. The view is of the base. The sides of the triangle measure 6 units, 8 units, and 8 units. The height of the pyramid is 5 units.

10. A cone of radius $r$ and height $h$ has a smaller cone of radius $r\text{/}2$ and height $h\text{/}2$ removed from the top, as seen here. The resulting solid is called a frustum.

This figure is a 3-dimensional graph of an upside down cone. The cone is inside of a rectangular prism that represents the xyz coordinate system. the radius of the bottom of the cone is “r” and the radius of the top of the cone is labeled “r/2”.

Show Solution

$\frac{7\pi }{12}h{r}^{2}$ units3

For the following exercises (11-16), draw an outline of the solid and find the volume using the slicing method.

11. The base is a circle of radius $a.$ The slices perpendicular to the base are squares.

12. The base is a triangle with vertices $(0,0),(1,0),$ and $(0,1).$ Slices perpendicular to the xy-plane are semicircles.

Show Solution

This figure shows the x-axis and the y-axis with a line starting on the x-axis at (1,0) and ending on the y-axis at (0,1). Perpendicular to the xy-plane are 4 shaded semi-circles with their diameters beginning on the x-axis and ending on the line, decreasing in size away from the origin.

\frac{π}{24}

$\frac{\pi }{24}$ units³

13. The base is the region under the parabola $y=1-{x}^{2}$ in the first quadrant. Slices perpendicular to the xy-plane are squares.

14. The base is the region under the parabola $y=1-{x}^{2}$ and above the $x\text{-axis}\text{.}$ Slices perpendicular to the $y\text{-axis}$ are squares.

Show Solution

15. The base is the region enclosed by $y={x}^{2}$ and $y=9.$ Slices perpendicular to the $x$ -axis are right isosceles triangles.

16. The base is the area between $y=x$ and $y={x}^{2}.$ Slices perpendicular to the $x$ -axis are semicircles.

Show Solution

This figure is a graph with the x and y axes diagonal to show 3-dimensional perspective. On the first quadrant of the graph are the curves y=x, a line, and y=x^2, a parabola. They intersect at the origin and at (1,1). Several semicircular-shaped shaded regions are perpendicular to the x y plane, which go from the parabola to the line and perpendicular to the line.

\frac{π}{240}

$\frac{\pi }{240}$ units³

For the following exercises (17-24), draw the region bounded by the curves. Then, use the disk method to find the volume when the region is rotated around the $x$ -axis.

17. $x+y=8,x=0,\text{ and }y=0$

18. $y=2{x}^{2},x=0,x=4,\text{ and }y=0$

Show Solution

This figure is a graph in the first quadrant. It is a shaded region bounded above by the curve y=2x^2, below by the x-axis, and to the right by the vertical line x=4.

\frac{4096 π}{5}

$\frac{4096\pi }{5}$ units³

19. $y={e}^{x}+1,x=0,x=1,\text{ and }y=0$

20. $y={x}^{4},x=0,\text{ and }y=1$

Show Solution

This figure is a graph in the first quadrant. It is a shaded region bounded above by the line y=1, below by the curve y=x^4, and to the left by the y-axis.

$\frac{8\pi }{9}$ units³

21. $y=\sqrt{x},x=0,x=4,\text{ and }y=0$

22. $y= \sin x,y= \cos x,\text{ and }x=0$

Show Solution

This figure is a shaded region bounded above by the curve y=cos(x), below to the left by the y-axis and below to the right by y=sin(x). The shaded region is in the first quadrant.

$\frac{\pi }{2}$ units³

23. $y=\frac{1}{x},x=2,\text{ and }y=3$

24. ${x}^{2}-{y}^{2}=9\text{ and }x+y=9,y=0\text{ and }x=0$

Show Solution

This figure is a graph in the first quadrant. It is a shaded region bounded above by the line x + y=9, below by the x-axis, to the left by the y-axis, and to the left by the curve x^2-y^2=9.

$207\pi$ units³

For the following exercises (25-32), draw the region bounded by the curves. Then, find the volume when the region is rotated around the $y$ -axis.

25. $y=4-\frac{1}{2}x,x=0,\text{ and }y=0$

26. $y=2{x}^{3},x=0,x=1,\text{ and }y=0$

Show Solution

This figure is a graph in the first quadrant. It is a shaded region bounded above by the curve y=2x^3, below by the x-axis, and to the right by the line x=1.

$\frac{4\pi }{5}$ units³

27. $y=3{x}^{2},x=0,\text{ and }y=3$

28. $y=\sqrt{4-{x}^{2}},y=0,\text{ and }x=0$

Show Solution

This figure is a graph in the first quadrant. It is a quarter of a circle with center at the origin and radius of 2. It is shaded on the inside.

$\frac{16\pi }{3}$ units³

29. $y=\frac{1}{\sqrt{x+1}},x=0,\text{ and }x=3$

30. $x= \sec (y)\text{ and }y=\frac{\pi }{4},y=0\text{ and }x=0$

Show Solution

This figure is a graph in the first quadrant. It is a shaded region bounded above by the line y=pi/4, to the right by the curve x=sec(y), below by the x-axis, and to the left by the y-axis.

$\pi$ units³

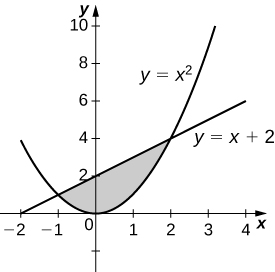
31. $y=\frac{1}{x+1},x=0,\text{ and }x=2$

32. $y=4-x,y=x,\text{ and }x=0$

Show Solution

This figure is a graph in the first quadrant. It is a shaded triangle bounded above by the line y=4-x, below by the line y=x, and to the left by the y-axis.

$\frac{16\pi }{3}$ units³

For the following exercises (33-40), draw the region bounded by the curves. Then, find the volume when the region is rotated around the $x$ -axis.

33. $y=x+2,y=x+6,x=0,\text{ and }x=5$

34. $y={x}^{2}\text{ and }y=x+2$

Show Solution

This figure is a graph above the x-axis. It is a shaded region bounded above by the line y=x+2, and below by the parabola y=x^2.

$\frac{72\pi }{5}$ units³

35. ${x}^{2}={y}^{3}\text{ and }{x}^{3}={y}^{2}$

36. $y=4-{x}^{2}\text{ and }y=2-x$

Show Solution

This figure is a shaded region bounded above by the curve y=4-x^2 and below by the line y=2-x.

$\frac{108\pi }{5}$ units³

37. [T] $y= \cos x,y={e}^{\text{−}x},x=0,\text{ and }x=1.2927$

38. $y=\sqrt{x}\text{ and }y={x}^{2}$

Show Solution

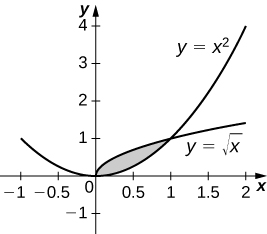
This figure is a graph in the first quadrant. It is a shaded region bounded above by the curve y=squareroot(x), below by the curve y=x^2.

$\frac{3\pi }{10}$ units³

39. $y= \sin x\text{,}y=5 \sin x,x=0\text{ and }x=\pi$

40. $y=\sqrt{1+{x}^{2}}\text{ and }y=\sqrt{4-{x}^{2}}$

Show Solution

This figure is a shaded region bounded above by the curve y=squareroot(4-x^2) and, below by the curve y=squareroot(1+x^2).

$2\sqrt{6}\pi$ units³

For the following exercises (41-45), draw the region bounded by the curves. Then, use the washer method to find the volume when the region is revolved around the $y$ -axis.

41. $y=\sqrt{x},x=4,\text{ and }y=0$

42. $y=x+2,y=2x-1,\text{ and }x=0$

Show Solution

This figure is a graph in the first quadrant. It is a shaded region bounded above by the line y=x+2, below by the line y=2x-1, and to the left by the y-axis.

$9\pi$ units³

43. $y=\sqrt[3]{x}\text{ and }y={x}^{3}$

44. $x={e}^{2y},x={y}^{2},y=0,\text{ and }y=\text{ln}(2)$

Show Solution

This figure is a graph in the first quadrant. It is a shaded region bounded above by the curve y=ln(2), below by the x-axis, to the left by the curve x=y^2, and to the right by the curve x=e^(2y).

$\frac{\pi }{20}(75-4{\text{ln}}^{5}(2))$ units³

45. $x=\sqrt{9-{y}^{2}},x={e}^{\text{−}y},y=0,\text{ and }y=3$

46. Yogurt containers can be shaped like frustums. Rotate the line $y=\frac{1}{m}x$ around the $y$ -axis to find the volume between $y=a\text{ and }y=b.$

This figure has two parts. The first part is a solid cone. The base of the cone is wider than the top. It is shown in a 3-dimensional box. Underneath the cone is an image of a yogurt container with the same shape as the figure.

Show Solution

$\frac{{m}^{2}\pi }{3}({b}^{3}-{a}^{3})$ units3

47. Rotate the ellipse $({x}^{2}\text{/}{a}^{2})+({y}^{2}\text{/}{b}^{2})=1$ around the $x$ -axis to approximate the volume of a football, as seen here.

This figure has an oval that is approximately equal to the image of a football.

48. Rotate the ellipse $({x}^{2}\text{/}{a}^{2})+({y}^{2}\text{/}{b}^{2})=1$ around the $y$ -axis to approximate the volume of a football.

Show Solution

$\frac{4{a}^{2}b\pi }{3}$ units³

49. A better approximation of the volume of a football is given by the solid that comes from rotating $y= \sin x$ around the $x$ -axis from $x=0$ to $x=\pi .$ What is the volume of this football approximation, as seen here?

This figure has a 3-dimensional oval shape. It is inside of a box parallel to the x-axis on the bottom front edge of the box. The y-axis is vertical to the solid.

50. What is the volume of the Bundt cake that comes from rotating $y= \sin x$ around the $y$ -axis from $x=0$ to $x=\pi ?$

This figure is a graph of a 3-dimensional solid. It is round, bigger towards the bottom. It has a hole in the center that progressively gets smaller towards the bottom. Next to the graph is an image of a bundt cake, resembling the solid.

Show Solution

$2{\pi }^{2}$ units3

For the following exercises (51-56), find the volume of the solid described.

51. The base is the region between $y=x$ and $y={x}^{2}.$ Slices perpendicular to the $x$ -axis are semicircles.

52. The base is the region enclosed by the generic ellipse $({x}^{2}\text{/}{a}^{2})+({y}^{2}\text{/}{b}^{2})=1.$ Slices perpendicular to the $x$ -axis are semicircles.

Show Solution

$\frac{2a{b}^{2}\pi }{3}$ units³

53. Bore a hole of radius $a$ down the axis of a right cone and through the base of radius $b,$ as seen here.

This figure is an upside down cone. It has a radius of the top as “b”, center at “a”, and height as “b”.

54. Find the volume common to two spheres of radius $r$ with centers that are $2h$ apart, as shown here.

This figure has two circles that intersect. Both circles have radius “r”. There is a line segment from one center to the other. In the middle of the intersection of the circles is point “h”. It is on the line segment.

Show Solution

$\frac{\pi }{12}{(r+h)}^{2}(6r-h)$ units3

55. Find the volume of a spherical cap of height $h$ and radius $r$ where [latex]h

This figure a portion of a sphere. This spherical cap has radius “r” and height “h”.

56. Find the volume of a sphere of radius $R$ with a cap of height $h$ removed from the top, as seen here.

This figure is a sphere with a top portion removed. The radius of the sphere is “R”. The distance from the center to where the top portion is removed is “R-h”.

Show Solution

$\frac{\pi }{3}(h+R){(h-2R)}^{2}$ units3

Applications of Integration: Supplemental Content

Problem Set: Determining Volumes by Slicing

Candela Citations