1. Why is [latex]u[/latex]-substitution referred to as change of variable?
2. If [latex]f=g\circ h,[/latex] when reversing the chain rule, [latex]\frac{d}{dx}(g\circ h)(x)={g}^{\prime }(h(x)){h}^{\prime }(x),[/latex] should you take [latex]u=g(x)[/latex] or [latex]u=h(x)?[/latex]
In the following exercises, verify each identity using differentiation. Then, using the indicated [latex]u[/latex]-substitution, identify [latex]f[/latex] such that the integral takes the form [latex]\displaystyle\int f(u)du.[/latex]
3. [latex]\displaystyle\int x\sqrt{x+1}dx=\frac{2}{15}{(x+1)}^{3\text{/}2}(3x-2)+C; \,\,\, u=x+1[/latex]
4. For [latex]x>1[/latex]: [latex]\displaystyle\int \frac{{x}^{2}}{\sqrt{x-1}}dx = \frac{2}{15}\sqrt{x-1}(3{x}^{2}+4x+8)+C; \,\,\, u=x-1[/latex]
5. [latex]\displaystyle\int x\sqrt{4{x}^{2}+9}dx=\frac{1}{12}{(4{x}^{2}+9)}^{3\text{/}2}+C; \,\,\, u=4{x}^{2}+9[/latex]
6. [latex]\displaystyle\int \frac{x}{\sqrt{4{x}^{2}+9}}dx=\frac{1}{4}\sqrt{4{x}^{2}+9}+C;\,\,\, u=4{x}^{2}+9[/latex]
7. [latex]\displaystyle\int \frac{x}{{(4{x}^{2}+9)}^{2}}dx=-\frac{1}{8(4{x}^{2}+9)};\,\,\, u=4{x}^{2}+9[/latex]
In the following exercises, find the antiderivative using the indicated substitution.
8. [latex]\displaystyle\int {(x+1)}^{4}dx; \,\,\, u=x+1[/latex]
9. [latex]\displaystyle\int {(x-1)}^{5}dx; \,\,\, u=x-1[/latex]
10. [latex]\displaystyle\int {(2x-3)}^{-7}dx; \,\,\, u=2x-3[/latex]
11. [latex]\displaystyle\int {(3x-2)}^{-11}dx; \,\,\, u=3x-2[/latex]
12. [latex]\displaystyle\int \frac{x}{\sqrt{{x}^{2}+1}}dx; \,\,\, u={x}^{2}+1[/latex]
13. [latex]\displaystyle\int \frac{x}{\sqrt{1-{x}^{2}}}dx; \,\,\, u=1-{x}^{2}[/latex]
14. [latex]\displaystyle\int (x-1){({x}^{2}-2x)}^{3}dx; \,\,\, u={x}^{2}-2x[/latex]
15. [latex]\displaystyle\int ({x}^{2}-2x){({x}^{3}-3{x}^{2})}^{2}dx; \,\,\, u={x}^{3}-3{x}^{2}[/latex]
16. [latex]\displaystyle\int { \cos }^{3}\theta d\theta ; \,\,\, u= \sin \theta [/latex]
17. [latex]\displaystyle\int { \sin }^{3}\theta d\theta ; \,\,\, u= \cos \theta [/latex]
In the following exercises, use a suitable change of variables to determine the indefinite integral.
18. [latex]\displaystyle\int x{(1-x)}^{99}dx[/latex]
19. [latex]\displaystyle\int t{(1-{t}^{2})}^{10}dt[/latex]
20. [latex]\displaystyle\int {(11x-7)}^{-3}dx[/latex]
21. [latex]\displaystyle\int {(7x-11)}^{4}dx[/latex]
22. [latex]\displaystyle\int { \cos }^{3}\theta \sin \theta d\theta [/latex]
23. [latex]\displaystyle\int { \sin }^{7}\theta \cos \theta d\theta [/latex]
24. [latex]\displaystyle\int { \cos }^{2}(\pi t) \sin (\pi t)dt[/latex]
25. [latex]\displaystyle\int { \sin }^{2}x{ \cos }^{3}xdx[/latex]
26. [latex]\displaystyle\int [latex]t[/latex] \sin ({t}^{2}) \cos ({t}^{2})dt[/latex]
27. [latex]\displaystyle\int {t}^{2}{ \cos }^{2}({t}^{3}) \sin ({t}^{3})dt[/latex]
28. [latex]\displaystyle\int \frac{{x}^{2}}{{({x}^{3}-3)}^{2}}dx[/latex]
29. [latex]\displaystyle\int \frac{{x}^{3}}{\sqrt{1-{x}^{2}}}dx[/latex]
30. [latex]\displaystyle\int \frac{{y}^{5}}{{(1-{y}^{3})}^{3\text{/}2}}dy[/latex]
31. [latex]{\displaystyle\int \cos \theta (1- \cos \theta )}^{99} \sin \theta d\theta [/latex]
32. [latex]{\displaystyle\int (1-{ \cos }^{3}\theta )}^{10}{ \cos }^{2}\theta \sin \theta d\theta [/latex]
33. [latex]\displaystyle\int ( \cos \theta -1){({ \cos }^{2}\theta -2 \cos \theta )}^{3} \sin \theta d\theta [/latex]
34. [latex]\displaystyle\int ({ \sin }^{2}\theta -2 \sin \theta ){({ \sin }^{3}\theta -3{ \sin }^{2}\theta )}^{3} \cos \theta d\theta [/latex]
In the following exercises, use a calculator to estimate the area under the curve using left Riemann sums with 50 terms, then use substitution to solve for the exact answer.
35. [T] [latex]y=3{(1-x)}^{2}[/latex] over [latex]\left[0,2\right][/latex]
36. [T] [latex]y=x{(1-{x}^{2})}^{3}[/latex] over [latex]\left[-1,2\right][/latex]
37. [T] [latex]y= \sin x{(1- \cos x)}^{2}[/latex] over [latex]\left[0,\pi \right][/latex]
38. [T] [latex]y=\dfrac{x}{{({x}^{2}+1)}^{2}}[/latex] over [latex]\left[-1,1\right][/latex]
In the following exercises, use a change of variables to evaluate the definite integral.
39. [latex]{\displaystyle\int }_{0}^{1}x\sqrt{1-{x}^{2}}dx[/latex]
40. [latex]{\displaystyle\int }_{0}^{1}\dfrac{x}{\sqrt{1+{x}^{2}}}dx[/latex]
41. [latex]{\displaystyle\int }_{0}^{2}\dfrac{t^2}{\sqrt{5+{t}^{2}}}dt[/latex]
42. [latex]{\displaystyle\int }_{0}^{1}\dfrac{t^2}{\sqrt{1+{t}^{3}}}dt[/latex]
43. [latex]{\displaystyle\int }_{0}^{\pi \text{/}4}{ \sec }^{2}\theta \tan \theta d\theta [/latex]
44. [latex]{\displaystyle\int }_{0}^{\pi \text{/}4}\dfrac{ \sin \theta }{{ \cos }^{4}\theta }d\theta [/latex]
In the following exercises, evaluate the indefinite integral [latex]\displaystyle\int f(x)dx[/latex] with constant [latex]C=0[/latex] using [latex]u[/latex]-substitution. Then, graph the function and the antiderivative over the indicated interval. If possible, estimate a value of C that would need to be added to the antiderivative to make it equal to the definite integral [latex]F(x)={\displaystyle\int }_{a}^{x}f(t)dt,[/latex] with [latex]a[/latex] the left endpoint of the given interval.
45. [T] [latex]\displaystyle\int (2x+1){e}^{{x}^{2}+x-6}dx[/latex] over [latex]\left[-3,2\right][/latex]
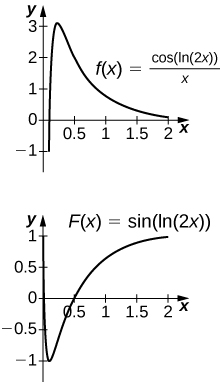
46. [T] [latex]\displaystyle\int \frac{ \cos (\text{ln}(2x))}{x}dx[/latex] on [latex]\left[0,2\right][/latex]
47. [T] [latex]\displaystyle\int \frac{3{x}^{2}+2x+1}{\sqrt{{x}^{3}+{x}^{2}+x+4}}dx[/latex] over [latex]\left[-1,2\right][/latex]
48. [T] [latex]\displaystyle\int \frac{ \sin x}{{ \cos }^{3}x}dx[/latex] over [latex]\left[-\frac{\pi }{3},\frac{\pi }{3}\right][/latex]
![Two graphs. The first is the function f(x) = sin(x) / cos(x)^3 over [-5pi/16, 5pi/16]. It is an increasing concave down function for values less than zero and an increasing concave up function for values greater than zero. The second is the fuction f(x) = ½ sec(x)^2 over the same interval. It is a wide, concave up curve which decreases for values less than zero and increases for values greater than zero.](https://s3-us-west-2.amazonaws.com/courses-images/wp-content/uploads/sites/2332/2018/01/11204239/CNX_Calc_Figure_05_05_206.jpg)
49. [T] [latex]\displaystyle\int (x+2){e}^{\text{−}{x}^{2}-4x+3}dx[/latex] over [latex]\left[-5,1\right][/latex]
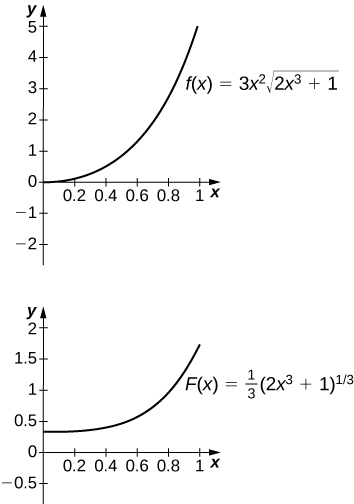
50. [T] [latex]\displaystyle\int 3{x}^{2}\sqrt{2{x}^{3}+1}dx[/latex] over [latex]\left[0,1\right][/latex]
51. If [latex]h(a)=h(b)[/latex] in [latex]{\displaystyle\int }_{a}^{b}g\text{‘}(h(x))h(x)dx,[/latex] what can you say about the value of the integral?
52. Is the substitution [latex]u=1-{x}^{2}[/latex] in the definite integral [latex]{\displaystyle\int }_{0}^{2}\dfrac{x}{1-{x}^{2}}dx[/latex] okay? If not, why not?
In the following exercises, use a change of variables to show that each definite integral is equal to zero.
53. [latex]{\displaystyle\int }_{0}^{\pi }{ \cos }^{2}(2\theta ) \sin (2\theta )d\theta [/latex]
54. [latex]{\displaystyle\int }_{0}^{\sqrt{\pi }}t \cos ({t}^{2}) \sin ({t}^{2})dt[/latex]
55. [latex]{\displaystyle\int }_{0}^{1}(1-2t)dt[/latex]
56. [latex]{\displaystyle\int }_{0}^{1}\dfrac{1-2t}{(1+{(t-\frac{1}{2})}^{2})}dt[/latex]
57. [latex]{\displaystyle\int }_{0}^{\pi } \sin ({(t-\frac{\pi }{2})}^{3}) \cos (t-\frac{\pi }{2})dt[/latex]
58. [latex]{\displaystyle\int }_{0}^{2}(1-t) \cos (\pi t)dt[/latex]
59. [latex]{\displaystyle\int }_{\pi \text{/}4}^{3\pi \text{/}4}{ \sin }^{2}t \cos tdt[/latex]
60. Show that the average value of [latex]f(x)[/latex] over an interval [latex]\left[a,b\right][/latex] is the same as the average value of [latex]f(cx)[/latex] over the interval [latex]\left[\frac{a}{c},\frac{b}{c}\right][/latex] for [latex]c>0.[/latex]
61. Find the area under the graph of [latex]f(t)=\dfrac{t}{{(1+{t}^{2})}^{a}}[/latex] between [latex]t=0[/latex] and [latex]t=x[/latex] where [latex]a>0[/latex] and [latex]a\ne 1[/latex] is fixed, and evaluate the limit as [latex]x\to \infty .[/latex]
62. Find the area under the graph of [latex]g(t)=\dfrac{t}{{(1-{t}^{2})}^{a}}[/latex] between [latex]t=0[/latex] and [latex]t=x,[/latex] where [latex]0<x<1[/latex] and [latex]a>0[/latex] is fixed. Evaluate the limit as [latex]x\to 1.[/latex]
63. The area of a semicircle of radius 1 can be expressed as [latex]{\displaystyle\int }_{-1}^{1}\sqrt{1-{x}^{2}}dx.[/latex] Use the substitution [latex]x= \cos t[/latex] to express the area of a semicircle as the integral of a trigonometric function. You do not need to compute the integral.
64. The area of the top half of an ellipse with a major axis that is the [latex]x[/latex]-axis from [latex]x=-1[/latex] to [latex]a[/latex] and with a minor axis that is the [latex]y[/latex]-axis from [latex]y=\text{−}b[/latex] to [latex]b[/latex] can be written as [latex]{\displaystyle\int }_{\text{−}a}^{a}b\sqrt{1-\frac{{x}^{2}}{{a}^{2}}}dx.[/latex] Use the substitution [latex]x=a \cos t[/latex] to express this area in terms of an integral of a trigonometric function. You do not need to compute the integral.
65. [T] The following graph is of a function of the form [latex]f(t)=a \sin (nt)+b \sin (mt).[/latex] Estimate the coefficients [latex]a[/latex] and [latex]b[/latex], and the frequency parameters [latex]n[/latex] and [latex]m[/latex]. Use these estimates to approximate [latex]{\displaystyle\int }_{0}^{\pi }f(t)dt.[/latex]
![A graph of a function of the given form over [0, 2pi], which has six turning points. They are located at just before pi/4, just after pi/2, between 3pi/4 and pi, between pi and 5pi/4, just before 3pi/2, and just after 7pi/4 at about 3, -2, 1, -1, 2, and -3. It begins at the origin and ends at (2pi, 0). It crosses the x-axis between pi/4 and pi/2, just before 3pi/4, pi, just after 5pi/4, and between 3pi/2 and 4pi/4.](https://s3-us-west-2.amazonaws.com/courses-images/wp-content/uploads/sites/2332/2018/01/11204247/CNX_Calc_Figure_05_05_201.jpg)
66. [T] The following graph is of a function of the form [latex]f(x)=a \cos (nt)+b \cos (mt).[/latex] Estimate the coefficients [latex]a[/latex] and [latex]b[/latex] and the frequency parameters [latex]n[/latex] and [latex]m[/latex]. Use these estimates to approximate [latex]{\displaystyle\int }_{0}^{\pi }f(t)dt.[/latex]
![The graph of a function of the given form over [0, 2pi]. It begins at (0,1) and ends at (2pi, 1). It has five turning points, located just after pi/4, between pi/2 and 3pi/4, pi, between 5pi/4 and 3pi/2, and just before 7pi/4 at about -1.5, 2.5, -3, 2.5, and -1. It crosses the x-axis between 0 and pi/4, just before pi/2, just after 3pi/4, just before 5pi/4, just after 3pi/2, and between 7pi/4 and 2pi.](https://s3-us-west-2.amazonaws.com/courses-images/wp-content/uploads/sites/2332/2018/01/11204249/CNX_Calc_Figure_05_05_202.jpg)
