Learning Outcomes
- Divide two fractions
- Divide a fraction by a whole number
- Determine whether a function is even, odd, or neither
In the Integration Formulas and the Net Change Theorem section, we will need skills that include how to simplify complex fractions and determine the symmetry of a function. These skills are reviewed here.
Simplify Complex Fractions
When integrating, it is not uncommon to have to work with a complex fraction, that is, a fraction that contains fractions in its numerator/denominator. An easy way to remember how to divide fractions is to multiply by the reciprocal. This means that you keep the first number as-is, change the division sign to multiplication, and then find the reciprocal of the second number (flip it!).
Example: Simplifying Complex Fractions
Simplify [latex]\dfrac{\frac{2}{3}}{\frac{1}{6}}[/latex].
Example: Simplifying Complex Fractions
Divide [latex]\dfrac{\frac{3}{5}}{2}[/latex].
Try It
Simplify [latex]\dfrac{\frac{5}{7}}{\frac{3}{8}}[/latex].
Determine Whether a Functions is Even, Odd, or Neither
Some functions exhibit symmetry so that reflections result in the original graph. For example, horizontally reflecting the toolkit functions [latex]f\left(x\right)={x}^{2}[/latex] or [latex]f\left(x\right)=|x|[/latex] will result in the original graph. We say that these types of graphs are symmetric about the [latex]y[/latex]-axis. Functions whose graphs are symmetric about the y-axis are called even functions.
If the graphs of [latex]f\left(x\right)={x}^{3}[/latex] or [latex]f\left(x\right)=\dfrac{1}{x}[/latex] were reflected over both axes, the result would be the original graph.
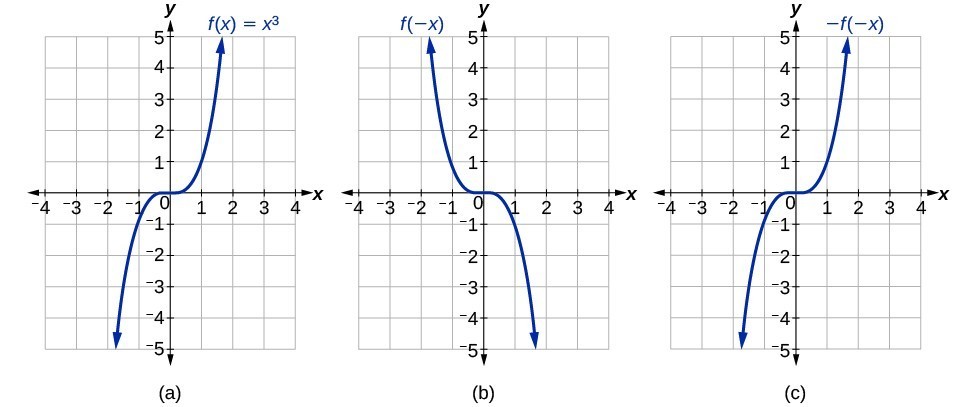
(a) The cubic toolkit function (b) Horizontal reflection of the cubic toolkit function (c) Horizontal and vertical reflections reproduce the original cubic function.
We say that these graphs are symmetric about the origin. A function with a graph that is symmetric about the origin is called an odd function.
Note: A function can be neither even nor odd if it does not exhibit either symmetry. For example, [latex]f\left(x\right)={2}^{x}[/latex] is neither even nor odd. Also, the only function that is both even and odd is the constant function [latex]f\left(x\right)=0[/latex].
You can view the transcript for “Introduction to Odd and Even Functions” here (opens in new window).
A General Note: Even and Odd Functions
A function is called an even function if for every input [latex]x[/latex]
[latex]f\left(x\right)=f\left(-x\right)[/latex]
The graph of an even function is symmetric about the [latex]y\text{-}[/latex] axis.
A function is called an odd function if for every input [latex]x[/latex]
[latex]f\left(x\right)=-f\left(-x\right)[/latex]
The graph of an odd function is symmetric about the origin.
How To: Given the formula for a function, determine if the function is even, odd, or neither.
- Determine whether the function satisfies [latex]f\left(x\right)=f\left(-x\right)[/latex]. If it does, it is even.
- Determine whether the function satisfies [latex]f\left(x\right)=-f\left(-x\right)[/latex]. If it does, it is odd.
- If the function does not satisfy either rule, it is neither even nor odd.
Example: Determining whether a Function Is Even, Odd, or Neither
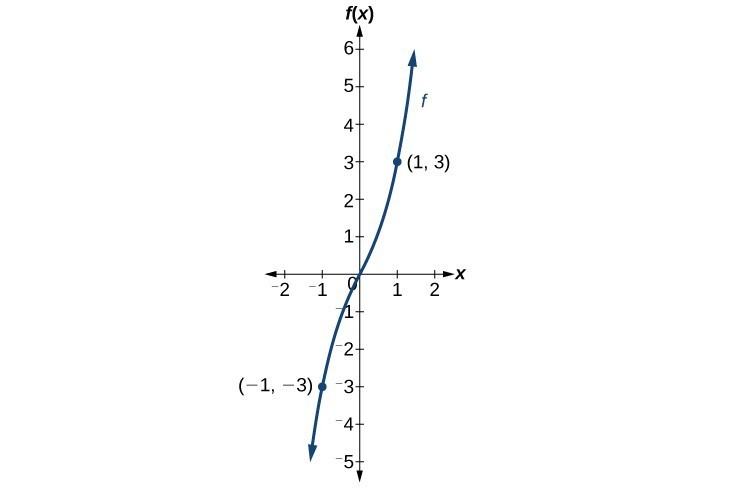
Is the function [latex]f\left(x\right)={x}^{3}+2x[/latex] even, odd, or neither?
Try It
Is the function [latex]f\left(s\right)={s}^{4}+3{s}^{2}+7[/latex] even, odd, or neither?
Try It
Candela Citations
- Modification and Revision . Provided by: Lumen Learning. License: CC BY: Attribution
- College Algebra Corequisite. Provided by: Lumen Learning. Located at: https://courses.lumenlearning.com/waymakercollegealgebracorequisite/. License: CC BY: Attribution
- Precalculus. Provided by: Lumen Learning. Located at: https://courses.lumenlearning.com/precalculus/. License: CC BY: Attribution