Learning Outcomes
- Find the distance between two points
- Find the midpoint of a line segment
- Complete the square
In the Conic Section section, we will learn about various conic sections including parabolas, ellipses, and hyperbolas. Here we will review how to use both the distance and midpoint formulas along with how to complete the square.
Find the Distance Between Two Points
A General Note: The Distance Formula
Given endpoints [latex]\left({x}_{1},{y}_{1}\right)[/latex] and [latex]\left({x}_{2},{y}_{2}\right)[/latex], the distance between two points is given by
Example: Finding the Distance between Two Points
Find the distance between the points [latex]\left(-3,-1\right)[/latex] and [latex]\left(2,3\right)[/latex].
Try It
Find the distance between two points: [latex]\left(1,4\right)[/latex] and [latex]\left(11,9\right)[/latex].
Find the Midpoint of a Line Segment
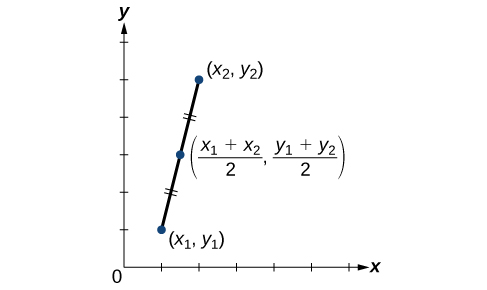
When the endpoints of a line segment are known, we can find the point midway between them. This point is known as the midpoint and the formula is known as the midpoint formula. Given the endpoints of a line segment, [latex]\left({x}_{1},{y}_{1}\right)[/latex] and [latex]\left({x}_{2},{y}_{2}\right)[/latex], the midpoint formula states how to find the coordinates of the midpoint [latex]M[/latex].
A graphical view of a midpoint is shown below. Notice that the line segments on either side of the midpoint are congruent.
Example: Finding the Midpoint of A Line Segment
Find the midpoint of the line segment with the endpoints [latex]\left(7,-2\right)[/latex] and [latex]\left(9,5\right)[/latex].
Try It
Find the midpoint of the line segment with endpoints [latex]\left(-2,-1\right)[/latex] and [latex]\left(-8,6\right)[/latex].
Try It
Complete the Square
(also in Module 3, Skills Review for Trigonometric Substitution)
We will use the example [latex]{x}^{2}+4x+1=0[/latex] to illustrate each step of completing the sqare. To complete the square, it is always easier when the leading coefficient, a, equals 1.
- Given a quadratic equation that cannot be factored and with [latex]a=1[/latex], first add or subtract the constant term to the right sign of the equal sign.
[latex]{x}^{2}+4x=-1[/latex]
- Multiply the b term by [latex]\frac{1}{2}[/latex] and square it.
[latex]\begin{array}{l}\frac{1}{2}\left(4\right)=2\hfill \\ {2}^{2}=4\hfill \end{array}[/latex]
- Add [latex]{\left(\frac{1}{2}b\right)}^{2}[/latex] to both sides of the equal sign and simplify the right side. We have
[latex]\begin{array}{l}{x}^{2}+4x+4=-1+4\hfill \\ {x}^{2}+4x+4=3\hfill \end{array}[/latex]
- The left side of the equation can now be factored as a perfect square.
[latex]\begin{array}{l}{x}^{2}+4x+4=3\hfill \\ {\left(x+2\right)}^{2}=3\hfill \end{array}[/latex]
- Use the square root property and solve.
[latex]\begin{array}{l}\sqrt{{\left(x+2\right)}^{2}}=\pm \sqrt{3}\hfill \\ x+2=\pm \sqrt{3}\hfill \\ x=-2\pm \sqrt{3}\hfill \end{array}[/latex]
- The solutions are [latex]x=-2+\sqrt{3}[/latex], [latex]x=-2-\sqrt{3}[/latex].
We will see when studying conic sections that the method of completing the square comes in handy when rewriting the equation of a conic section given in general form. In preparation to use the method in this manner, it will be good to practice it first.
How To: use the method of complete the square to write a perfect square trinomial from an expression
- Given an expression of the form [latex]a\left(x^2+bx\right)[/latex], add [latex]\left(\dfrac{b}{2}\right)^2[/latex] inside the parentheses.
- Then subtract [latex]a\left(\dfrac{b}{2}\right)^2[/latex] to counteract the change you made to the expression.
- If completing the square on one side of an equation, you may either subtract the value of [latex]a\left(\dfrac{b}{2}\right)^2[/latex] from that side, or add it to the other to maintain equality.
- Then factor the perfect square trinomial you created inside the original parentheses.
The resulting form will look like this:
Given
[latex]\qquad a\left(x^2+bx\right)[/latex]
add [latex]\left(b/2\right)^2[/latex] inside the parentheses and subtract [latex]a\left(b/2\right)^2[/latex] to counteract the change you made to the expression
[latex]=a\left(x^2+bx+ \left(\dfrac{b}{2}\right)^2\right)-a\left(\dfrac{b}{2}\right)^2[/latex]
then factor the resulting perfect square trinomial
[latex]=a\left(x+ \dfrac{b}{2}\right)^2-a\left(\dfrac{b}{2}\right)^2[/latex].
Example : CreatING a perfect square trinomial using the method of complete the square
Complete the square on: [latex]3\left(x^2 - 10x\right)[/latex].
try it
Candela Citations
- Modification and Revision. Provided by: Lumen Learning. License: CC BY: Attribution
- College Algebra Corequisite. Provided by: Lumen Learning. Located at: https://courses.lumenlearning.com/waymakercollegealgebracorequisite/. License: CC BY: Attribution
- Precalculus. Provided by: Lumen Learning. Located at: https://courses.lumenlearning.com/precalculus/. License: CC BY: Attribution

