Skills Review for Improper Integrals

Learning Outcomes

Calculate the limit of a function as 𝑥 increases or decreases without bound
Recognize when to apply L’Hôpital’s rule
Identify indeterminate forms produced by quotients, products, subtractions, and powers, and apply L’Hôpital’s rule in each case

In the Improper Integrals section, we will be faced with evaluating integrals that contain bounds that are either infinite or where the function we are integrating is undefined. As a result, here we will review how to find limits of functions at infinity and apply L’Hopital’s Rule.

Limits at Infinity

Recall that $\underset{x \to a}{\lim}f(x)=L$ means $f(x)$ becomes arbitrarily close to $L$ as long as $x$ is sufficiently close to $a$ . We can extend this idea to limits at infinity. For example, consider the function $f(x)=2+\frac{1}{x}$ . As can be seen graphically below, as the values of $x$ get larger, the values of $f(x)$ approach 2. We say the limit as $x$ approaches $\infty$ of $f(x)$ is 2 and write $\underset{x\to \infty }{\lim}f(x)=2$ . Similarly, for $x<0$ , as the values $|x|$ get larger, the values of $f(x)$ approaches 2. We say the limit as $x$ approaches $−\infty$ of $f(x)$ is 2 and write $\underset{x\to a}{\lim}f(x)=2$ .

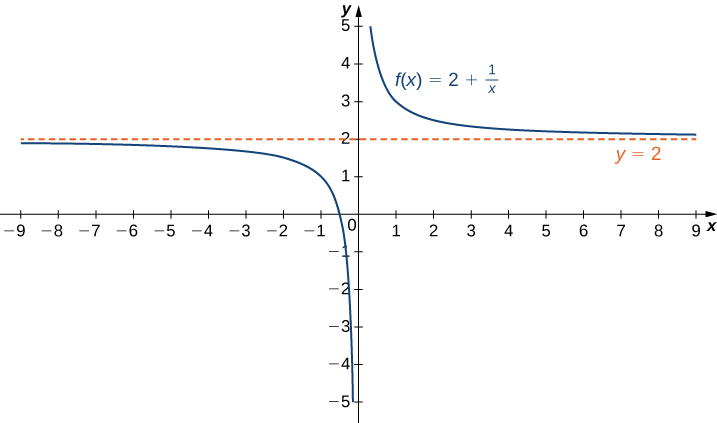
The function f(x) 2 + 1/x is graphed. The function starts negative near y = 2 but then decreases to −∞ near x = 0. The function then decreases from ∞ near x = 0 and gets nearer to y = 2 as x increases. There is a horizontal line denoting the asymptote y = 2.

The function approaches the asymptote $y=2$ as $x$ approaches $\pm \infty$ .

More generally, for any function $f$ , we say the limit as $x \to \infty$ of $f(x)$ is $L$ if $f(x)$ becomes arbitrarily close to $L$ as long as $x$ is sufficiently large. In that case, we write $\underset{x\to \infty}{\lim}f(x)=L$ . Similarly, we say the limit as $x\to −\infty$ of $f(x)$ is $L$ if $f(x)$ becomes arbitrarily close to $L$ as long as $x<0$ and $|x|$ is sufficiently large. In that case, we write $\underset{x\to −\infty }{\lim}f(x)=L$ . We now look at the definition of a function having a limit at infinity.

Definition

(Informal) If the values of $f(x)$ become arbitrarily close to $L$ as $x$ becomes sufficiently large, we say the function $f$ has a limit at infinity and write

$\underset{x\to \infty }{\lim}f(x)=L$

If the values of $f(x)$ becomes arbitrarily close to $L$ for $x<0$ as $|x|$ becomes sufficiently large, we say that the function $f$ has a limit at negative infinity and write

$\underset{x\to -\infty }{\lim}f(x)=L$

Example: Computing Limits at Infinity

For each of the following functions $f$ , evaluate $\underset{x\to \infty }{\lim}f(x)$ and $\underset{x\to −\infty }{\lim}f(x)$ .

$f(x)=5-\frac{2}{x^2}$
$f(x)=\dfrac{\sin x}{x}$

Show Solution

Using the algebraic limit laws, we have $\underset{x\to \infty }{\lim}(5-\frac{2}{x^2})=\underset{x\to \infty }{\lim}5-2(\underset{x\to \infty }{\lim}\frac{1}{x})(\underset{x\to \infty }{\lim}\frac{1}{x})=5-2 \cdot 0=5$ . Similarly, $\underset{x\to -\infty }{\lim}f(x)=5$ .
nce $-1\le \sin x\le 1$ for all $x$ , we have
$\frac{-1}{x}\le \frac{\sin x}{x}\le \frac{1}{x}$

for all $x \ne 0$ . Also, since

$\underset{x\to \infty }{\lim}\frac{-1}{x}=0=\underset{x\to \infty }{\lim}\frac{1}{x}$ ,

we can apply the squeeze theorem to conclude that

$\underset{x\to \infty }{\lim}\frac{\sin x}{x}=0$

Similarly,

$\underset{x\to −\infty}{\lim}\frac{\sin x}{x}=0$

Try It

Evaluate $\underset{x\to −\infty}{\lim}\left(3+\frac{4}{x}\right)$ and $\underset{x\to \infty }{\lim}\left(3+\frac{4}{x}\right)$ .

Hint

$\underset{x\to \pm \infty }{\lim}1/x=0$

Show Solution

Sometimes the values of a function $f$ become arbitrarily large as $x\to \infty$ (or as $x\to −\infty )$ . In this case, we write $\underset{x\to \infty }{\lim}f(x)=\infty$ (or $\underset{x\to −\infty }{\lim}f(x)=\infty )$ . On the other hand, if the values of $f$ are negative but become arbitrarily large in magnitude as $x\to \infty$ (or as $x\to −\infty )$ , we write $\underset{x\to \infty }{\lim}f(x)=−\infty$ (or $\underset{x\to −\infty }{\lim}f(x)=−\infty )$ .

For example, consider the function $f(x)=x^3$ . The $\underset{x\to \infty }{\lim}x^3=\infty$ . On the other hand, as $x\to −\infty$ , the values of $f(x)=x^3$ are negative but become arbitrarily large in magnitude. Consequently, $\underset{x\to −\infty }{\lim}x^3=−\infty$ .

Values of a power function as $x\to \pm \infty$
$x$	10	20	50	100	1000
$x^3$	1000	8000	125,000	1,000,000	1,000,000,000
$x$	-10	-20	-50	-100	-1000
$x^3$	-1000	-8000	-125,000	-1,000,000	-1,000,000,000

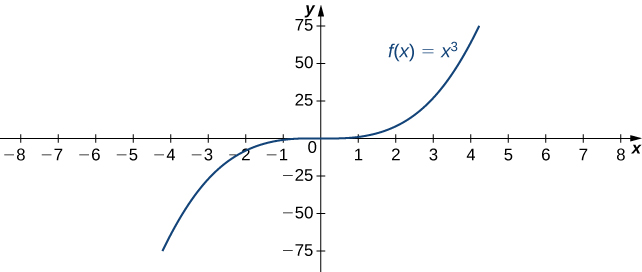
The function f(x) = x3 is graphed. It is apparent that this function rapidly approaches infinity as x approaches infinity.

For this function, the functional values approach infinity as $x\to \pm \infty$ .

Definition

(Informal) We say a function $f$ has an infinite limit at infinity and write

$\underset{x\to \infty }{\lim}f(x)=\infty$

if $f(x)$ becomes arbitrarily large for $x$ sufficiently large. We say a function has a negative infinite limit at infinity and write

$\underset{x\to \infty }{\lim}f(x)=−\infty$

if $f(x)<0$ and $|f(x)|$ becomes arbitrarily large for $x$ sufficiently large. Similarly, we can define infinite limits as $x\to −\infty$ .

Apply L’Hopital’s Rule

Indeterminate Form of Type $\frac{0}{0}$

L’Hôpital’s rule can be used to evaluate limits involving the quotient of two functions. Consider

$\underset{x\to a}{\lim}\dfrac{f(x)}{g(x)}$

If $\underset{x\to a}{\lim}f(x)=L_1$ and $\underset{x\to a}{\lim}g(x)=L_2 \ne 0$ , then

$\underset{x\to a}{\lim}\dfrac{f(x)}{g(x)}=\dfrac{L_1}{L_2}$

However, what happens if $\underset{x\to a}{\lim}f(x)=0$ and $\underset{x\to a}{\lim}g(x)=0$ ? We call this one of the indeterminate forms, of type $\frac{0}{0}$ . This is considered an indeterminate form because we cannot determine the exact behavior of $\frac{f(x)}{g(x)}$ as $x\to a$ without further analysis.

L’Hôpital’s Rule (0/0 Case)

Suppose $f$ and $g$ are differentiable functions over an open interval containing $a$ , except possibly at $a$ . If $\underset{x\to a}{\lim}f(x)=0$ and $\underset{x\to a}{\lim}g(x)=0$ , then

$\underset{x\to a}{\lim}\dfrac{f(x)}{g(x)}=\underset{x\to a}{\lim}\dfrac{f^{\prime}(x)}{g^{\prime}(x)}$ ,

assuming the limit on the right exists or is $\infty$ or $−\infty$ . This result also holds if we are considering one-sided limits, or if $a=\infty$ or $-\infty$ .

Example: Applying L’Hôpital’s Rule (0/0 Case)

Evaluate each of the following limits by applying L’Hôpital’s rule.

$\underset{x\to 0}{\lim}\dfrac{1- \cos x}{x}$
$\underset{x\to 1}{\lim}\dfrac{\sin (\pi x)}{\ln x}$
$\underset{x\to \infty }{\lim}\dfrac{e^{\frac{1}{x}}-1}{\frac{1}{x}}$
$\underset{x\to 0}{\lim}\dfrac{\sin x-x}{x^2}$

Show Solution

Since the numerator $1- \cos x\to 0$ and the denominator $x\to 0$ , we can apply L’Hôpital’s rule to evaluate this limit. We have
$\begin{array}{ll} \underset{x\to 0}{\lim}\frac{1- \cos x}{x} & =\underset{x\to 0}{\lim}\frac{\frac{d}{dx}(1- \cos x)}{\frac{d}{dx}(x)} \\ & =\underset{x\to 0}{\lim}\frac{\sin x}{1} \\ & =\frac{\underset{x\to 0}{\lim}(\sin x)}{\underset{x\to 0}{\lim}(1)} \\ & =\frac{0}{1}=0 \end{array}$
As $x\to 1$ , the numerator $\sin (\pi x)\to 0$ and the denominator $\ln x \to 0$ . Therefore, we can apply L’Hôpital’s rule. We obtain
$\begin{array}{ll} \underset{x\to 1}{\lim}\frac{\sin (\pi x)}{\ln x} & =\underset{x\to 1}{\lim}\frac{\pi \cos (\pi x)}{1/x} \\ & =\underset{x\to 1}{\lim}(\pi x) \cos (\pi x) \\ & =(\pi \cdot 1)(-1)=−\pi \end{array}$
As $x\to \infty$ , the numerator $e^{1/x}-1\to 0$ and the denominator $(\frac{1}{x})\to 0$ . Therefore, we can apply L’Hôpital’s rule. We obtain
$\underset{x\to \infty }{\lim}\frac{e^{1/x}-1}{\frac{1}{x}}=\underset{x\to \infty }{\lim}\frac{e^{1/x}(\frac{-1}{x^2})}{(\frac{-1}{x^2})}=\underset{x\to \infty}{\lim} e^{1/x}=e^0=1$
As $x\to 0$ , both the numerator and denominator approach zero. Therefore, we can apply L’Hôpital’s rule. We obtain
$\underset{x\to 0}{\lim}\frac{\sin x-x}{x^2}=\underset{x\to 0}{\lim}\frac{\cos x-1}{2x}$ .

Since the numerator and denominator of this new quotient both approach zero as $x\to 0$ , we apply L’Hôpital’s rule again. In doing so, we see that

$\underset{x\to 0}{\lim}\frac{\cos x-1}{2x}=\underset{x\to 0}{\lim}\frac{−\sin x}{2}=0$ .

Therefore, we conclude that

$\underset{x\to 0}{\lim}\frac{\sin x-x}{x^2}=0$ .

Try It

Evaluate $\underset{x\to 0}{\lim}\dfrac{x}{\tan x}$ .

Hint

$\frac{d}{dx} \tan x= \sec ^2 x$

Show Solution

$1$

Indeterminate Form of Type $\frac{\infty}{\infty}$

We can also use L’Hôpital’s rule to evaluate limits of quotients $\frac{f(x)}{g(x)}$ in which $f(x)\to \pm \infty$ and $g(x)\to \pm \infty$ . Limits of this form are classified as indeterminate forms of type $\infty / \infty$ . Again, note that we are not actually dividing $\infty$ by $\infty$ . Since $\infty$ is not a real number, that is impossible; rather, $\infty / \infty$ is used to represent a quotient of limits, each of which is $\infty$ or $−\infty$ .

L’Hôpital’s Rule ( $\infty / \infty$ Case)

Suppose $f$ and $g$ are differentiable functions over an open interval containing $a$ , except possibly at $a$ . Suppose $\underset{x\to a}{\lim}f(x)=\infty$ (or $−\infty$ ) and $\underset{x\to a}{\lim}g(x)=\infty$ (or $−\infty$ ). Then,

$\underset{x\to a}{\lim}\dfrac{f(x)}{g(x)}=\underset{x\to a}{\lim}\dfrac{f^{\prime}(x)}{g^{\prime}(x)}$ ,

assuming the limit on the right exists or is $\infty$ or $−\infty$ . This result also holds if the limit is infinite, if $a=\infty$ or $−\infty$ , or the limit is one-sided.

Example: Applying L’Hôpital’s Rule ( $\infty /\infty$ Case)

Evaluate each of the following limits by applying L’Hôpital’s rule.

$\underset{x\to \infty }{\lim}\dfrac{3x+5}{2x+1}$
$\underset{x\to 0^+}{\lim}\dfrac{\ln x}{\cot x}$

Show Solution

Since $3x+5$ and $2x+1$ are first-degree polynomials with positive leading coefficients, $\underset{x\to \infty }{\lim}(3x+5)=\infty$ and $\underset{x\to \infty }{\lim}(2x+1)=\infty$ . Therefore, we apply L’Hôpital’s rule and obtain
$\underset{x\to \infty}{\lim}\dfrac{3x+5}{2x+\frac{1}{x}}=\underset{x\to \infty }{\lim}\dfrac{3}{2}=\dfrac{3}{2}$ .

Note that this limit can also be calculated without invoking L’Hôpital’s rule. Earlier in the module we showed how to evaluate such a limit by dividing the numerator and denominator by the highest power of $x$ in the denominator. In doing so, we saw that

$\underset{x\to \infty }{\lim}\dfrac{3x+5}{2x+1}=\underset{x\to \infty }{\lim}\dfrac{3+\frac{5}{x}}{2+\frac{1}{x}}=\dfrac{3}{2}$ .

L’Hôpital’s rule provides us with an alternative means of evaluating this type of limit.
Here, $\underset{x\to 0^+}{\lim} \ln x=−\infty$ and $\underset{x\to 0^+}{\lim} \cot x=\infty$ . Therefore, we can apply L’Hôpital’s rule and obtain
$\underset{x\to 0^+}{\lim}\dfrac{\ln x}{\cot x}=\underset{x\to 0^+}{\lim}\dfrac{\frac{1}{x}}{−\csc^2 x}=\underset{x\to 0^+}{\lim}\dfrac{1}{−x \csc^2 x}$ .

Now as $x\to 0^+$ , $\csc^2 x\to \infty$ . Therefore, the first term in the denominator is approaching zero and the second term is getting really large. In such a case, anything can happen with the product. Therefore, we cannot make any conclusion yet. To evaluate the limit, we use the definition of $\csc x$ to write

$\underset{x\to 0^+}{\lim}\dfrac{1}{−x \csc^2 x}=\underset{x\to 0^+}{\lim}\dfrac{\sin^2 x}{−x}$ .

Now $\underset{x\to 0^+}{\lim} \sin^2 x=0$ and $\underset{x\to 0^+}{\lim} x=0$ , so we apply L’Hôpital’s rule again. We find

$\underset{x\to 0^+}{\lim}\dfrac{\sin^2 x}{−x}=\underset{x\to 0^+}{\lim}\dfrac{2 \sin x \cos x}{-1}=\dfrac{0}{-1}=0$ .

We conclude that

$\underset{x\to 0^+}{\lim}\dfrac{\ln x}{\cot x}=0$ .

Try It

Evaluate $\underset{x\to \infty }{\lim}\dfrac{\ln x}{5x}$

Hint

$\frac{d}{dx}\ln x=\frac{1}{x}$

Show Solution

L’Hôpital’s rule is very useful for evaluating limits involving the indeterminate forms $\frac{0}{0}$ and $\frac{\infty}{\infty}$ . However, we can also use L’Hôpital’s rule to help evaluate limits involving other indeterminate forms that arise when evaluating limits. The expressions $0 \cdot \infty$ , $\infty - \infty$ , $1^{\infty}$ , $\infty^0$ , and $0^0$ are all considered indeterminate forms. These expressions are not real numbers. Rather, they represent forms that arise when trying to evaluate certain limits. Next we realize why these are indeterminate forms and then understand how to use L’Hôpital’s rule in these cases. The key idea is that we must rewrite the indeterminate forms in such a way that we arrive at the indeterminate form $\frac{0}{0}$ or $\frac{\infty}{\infty}$ .

Indeterminate Form of Type $0 \cdot \infty$

Suppose we want to evaluate $\underset{x\to a}{\lim}(f(x) \cdot g(x))$ , where $f(x)\to 0$ and $g(x)\to \infty$ (or $−\infty$ ) as $x\to a$ . Since one term in the product is approaching zero but the other term is becoming arbitrarily large (in magnitude), anything can happen to the product. We use the notation $0 \cdot \infty$ to denote the form that arises in this situation. The expression $0 \cdot \infty$ is considered indeterminate because we cannot determine without further analysis the exact behavior of the product $f(x)g(x)$ as $x\to {a}$ . For example, let $n$ be a positive integer and consider

$f(x)=\dfrac{1}{(x^n+1)}$ and

$g(x)=3x^2$ .

As $x\to \infty$ , $f(x)\to 0$ and $g(x)\to \infty$ . However, the limit as $x\to \infty$ of $f(x)g(x)=\frac{3x^2}{(x^n+1)}$ varies, depending on $n$ . If $n=2$ , then $\underset{x\to \infty }{\lim}f(x)g(x)=3$ . If $n=1$ , then $\underset{x\to \infty }{\lim}f(x)g(x)=\infty$ . If $n=3$ , then $\underset{x\to \infty }{\lim}f(x)g(x)=0$ . Here we consider another limit involving the indeterminate form $0 \cdot \infty$ and show how to rewrite the function as a quotient to use L’Hôpital’s rule.

Example: Indeterminate Form of Type $0·\infty$

Evaluate $\underset{x\to 0^+}{\lim}x \ln x$

Show Solution

First, rewrite the function $x \ln x$ as a quotient to apply L’Hôpital’s rule. If we write

$x \ln x=\frac{\ln x}{1/x}$ ,

we see that $\ln x\to −\infty$ as $x\to 0^+$ and $\frac{1}{x}\to \infty$ as $x\to 0^+$ . Therefore, we can apply L’Hôpital’s rule and obtain

$\underset{x\to 0^+}{\lim}\frac{\ln x}{1/x}=\underset{x\to 0^+}{\lim}\frac{\frac{d}{dx}(\ln x)}{\frac{d}{dx}(1/x)}=\underset{x\to 0^+}{\lim}\frac{1/x}{-1/x^2}=\underset{x\to 0^+}{\lim}(−x)=0$ .

We conclude that

$\underset{x\to 0^+}{\lim}x \ln x=0$ .

The function y = x ln(x) is graphed for values x ≥ 0. At x = 0, the value of the function is 0.

Finding the limit at $x=0$ of the function $f(x)=x \ln x$ .

Try It

Evaluate $\underset{x\to 0}{\lim}x \cot x$

Hint

Write $x \cot x=\frac{x \cos x}{\sin x}$

Show Solution

Indeterminate Form of Type $\infty -\infty$

Another type of indeterminate form is $\infty -\infty$ . Consider the following example. Let $n$ be a positive integer and let $f(x)=3x^n$ and $g(x)=3x^2+5$ . As $x\to \infty$ , $f(x)\to \infty$ and $g(x)\to \infty$ . We are interested in $\underset{x\to \infty}{\lim}(f(x)-g(x))$ . Depending on whether $f(x)$ grows faster, $g(x)$ grows faster, or they grow at the same rate, as we see next, anything can happen in this limit. Since $f(x)\to \infty$ and $g(x)\to \infty$ , we write $\infty -\infty$ to denote the form of this limit. As with our other indeterminate forms, $\infty -\infty$ has no meaning on its own and we must do more analysis to determine the value of the limit. For example, suppose the exponent $n$ in the function $f(x)=3x^n$ is $n=3$ , then

$\underset{x\to \infty }{\lim}(f(x)-g(x))=\underset{x\to \infty }{\lim}(3x^3-3x^2-5)=\infty$ .

On the other hand, if $n=2$ , then

$\underset{x\to \infty }{\lim}(f(x)-g(x))=\underset{x\to \infty }{\lim}(3x^2-3x^2-5)=-5$ .

However, if $n=1$ , then

$\underset{x\to \infty }{\lim}(f(x)-g(x))=\underset{x\to \infty }{\lim}(3x-3x^2-5)=−\infty$ .

Therefore, the limit cannot be determined by considering only $\infty -\infty$ . Next we see how to rewrite an expression involving the indeterminate form $\infty -\infty$ as a fraction to apply L’Hôpital’s rule.

Example: Indeterminate Form of Type $\infty -\infty$

Evaluate $\underset{x\to 0^+}{\lim}\left(\dfrac{1}{x^2}-\dfrac{1}{\tan x}\right)$ .

Show Solution

By combining the fractions, we can write the function as a quotient. Since the least common denominator is $x^2 \tan x$ , we have

$\frac{1}{x^2}-\frac{1}{\tan x}=\frac{(\tan x)-x^2}{x^2 \tan x}$

As $x\to 0^+$ , the numerator $\tan x-x^2 \to 0$ and the denominator $x^2 \tan x \to 0$ . Therefore, we can apply L’Hôpital’s rule. Taking the derivatives of the numerator and the denominator, we have

$\underset{x\to 0^+}{\lim}\frac{(\tan x)-x^2}{x^2 \tan x}=\underset{x\to 0^+}{\lim}\frac{(\sec^2 x)-2x}{x^2 \sec^2 x+2x \tan x}$

As $x\to 0^+$ , $(\sec^2 x)-2x \to 1$ and $x^2 \sec^2 x+2x \tan x \to 0$ . Since the denominator is positive as $x$ approaches zero from the right, we conclude that

$\underset{x\to 0^+}{\lim}\frac{(\sec^2 x)-2x}{x^2 \sec^2 x+2x \tan x}=\infty$

Therefore,

$\underset{x\to 0^+}{\lim}(\frac{1}{x^2}-\frac{1}{ tan x})=\infty$

Try It

Evaluate $\underset{x\to 0^+}{\lim}\left(\dfrac{1}{x}-\dfrac{1}{\sin x}\right)$ .

Hint

Show Solution

Other Types of Indeterminate Form

Another type of indeterminate form that arises when evaluating limits involves exponents. The expressions $0^0$ , $\infty^0$ , and $1^{\infty}$ are all indeterminate forms. On their own, these expressions are meaningless because we cannot actually evaluate these expressions as we would evaluate an expression involving real numbers. Rather, these expressions represent forms that arise when finding limits. Now we examine how L’Hôpital’s rule can be used to evaluate limits involving these indeterminate forms.

Since L’Hôpital’s rule applies to quotients, we use the natural logarithm function and its properties to reduce a problem evaluating a limit involving exponents to a related problem involving a limit of a quotient. For example, suppose we want to evaluate $\underset{x\to a}{\lim}f(x)^{g(x)}$ and we arrive at the indeterminate form $\infty^0$ . (The indeterminate forms $0^0$ and $1^{\infty}$ can be handled similarly.)

Example: Indeterminate Form of Type $\infty^0$

Evaluate $\underset{x\to \infty }{\lim} x^{\frac{1}{x}}$

Show Solution

Let $y=x^{1/x}$ . Then,

$\ln (x^{1/x})=\frac{1}{x} \ln x=\frac{\ln x}{x}$

We need to evaluate $\underset{x\to \infty }{\lim}\frac{\ln x}{x}$ . Applying L’Hôpital’s rule, we obtain

$\underset{x\to \infty }{\lim} \ln y=\underset{x\to \infty}{\lim}\frac{\ln x}{x}=\underset{x\to \infty}{\lim}\frac{1/x}{1}=0$

Therefore, $\underset{x\to \infty }{\lim}\ln y=0$ . Since the natural logarithm function is continuous, we conclude that

$\ln (\underset{x\to \infty}{\lim} y)=0$ ,

which leads to

$\underset{x\to \infty }{\lim} y=\underset{x\to \infty}{\lim}\frac{\ln x}{x}=e^0=1$

Hence,

$\underset{x\to \infty}{\lim} x^{1/x}=1$

Try It

Evaluate $\underset{x\to \infty}{\lim} x^{\frac{1}{\ln x}}$

Hint

Let $y=x^{1/ \ln x}$ and apply the natural logarithm to both sides of the equation.

Show Solution

$e$

Example: Indeterminate Form of Type $0^0$

Evaluate $\underset{x\to 0^+}{\lim} x^{\sin x}$

Show Solution

Let

$y=x^{\sin x}$

Therefore,

$\ln y=\ln (x^{\sin x})= \sin x \ln x$

We now evaluate $\underset{x\to 0^+}{\lim} \sin x \ln x$ . Since $\underset{x\to 0^+}{\lim} \sin x=0$ and $\underset{x\to 0^+}{\lim} \ln x=−\infty$ , we have the indeterminate form $0 \cdot \infty$ . To apply L’Hôpital’s rule, we need to rewrite $\sin x \ln x$ as a fraction. We could write

$\sin x \ln x=\frac{\sin x}{1/ \ln x}$

$\sin x \ln x=\frac{\ln x}{1/ \sin x}=\frac{\ln x}{\csc x}$

Let’s consider the first option. In this case, applying L’Hôpital’s rule, we would obtain

$\underset{x\to 0^+}{\lim} \sin x \ln x=\underset{x\to 0^+}{\lim}\frac{\sin x}{1/ \ln x}=\underset{x\to 0^+}{\lim}\frac{\cos x}{-1/(x(\ln x)^2)}=\underset{x\to 0^+}{\lim}(−x(\ln x)^2 \cos x)$

Unfortunately, we not only have another expression involving the indeterminate form $0 \cdot \infty$ , but the new limit is even more complicated to evaluate than the one with which we started. Instead, we try the second option. By writing

$\sin x \ln x=\frac{\ln x}{1/ \sin x}=\frac{\ln x}{\csc x}$

and applying L’Hôpital’s rule, we obtain

$\underset{x\to 0^+}{\lim} \sin x \ln x=\underset{x\to 0^+}{\lim}\frac{\ln x}{\csc x}=\underset{x\to 0^+}{\lim}\frac{1/x}{− \csc x \cot x}=\underset{x\to 0^+}{\lim}\frac{-1}{x \csc x \cot x}$

Using the fact that $\csc x=\frac{1}{\sin x}$ and $\cot x=\frac{\cos x}{\sin x}$ , we can rewrite the expression on the right-hand side as

$\underset{x\to 0^+}{\lim}\frac{−\sin^2 x}{x \cos x}=\underset{x\to 0^+}{\lim}[\frac{\sin x}{x} \cdot (−\tan x)]=(\underset{x\to 0^+}{\lim}\frac{\sin x}{x}) \cdot (\underset{x\to 0^+}{\lim}(−\tan x))=1 \cdot 0=0$

We conclude that $\underset{x\to 0^+}{\lim} \ln y=0$ . Therefore, $\ln (\underset{x\to 0^+}{\lim} y)=0$ and we have

$\underset{x\to 0^+}{\lim} y=\underset{x\to 0^+}{\lim} x^{\sin x}=e^0=1$

Hence,

$\underset{x\to 0^+}{\lim} x^{\sin x}=1$

Try It

Evaluate $\underset{x\to 0^+}{\lim} x^x$

Hint

Let $y=x^x$ and take the natural logarithm of both sides of the equation.

Show Solution

Techniques of Integration: Prerequisite Material