Learning Objectives
- Identify a cylinder as a type of three-dimensional surface.
The first surface we’ll examine is the cylinder. Although most people immediately think of a hollow pipe or a soda straw when they hear the word cylinder, here we use the broad mathematical meaning of the term. As we have seen, cylindrical surfaces don’t have to be circular. A rectangular heating duct is a cylinder, as is a rolled-up yoga mat, the cross-section of which is a spiral shape.
In the two-dimensional coordinate plane, the equation [latex]x^{2}+y^{2}=9[/latex] describes a circle centered at the origin with radius 3. In three-dimensional space, this same equation represents a surface. Imagine copies of a circle stacked on top of each other centered on the [latex]z[/latex]-axis (Figure 1), forming a hollow tube. We can then construct a cylinder from the set of lines parallel to the [latex]z[/latex]-axis passing through circle [latex]x^{2}+y^{2}=9[/latex] in the [latex]xy[/latex]-plane, as shown in the figure. In this way, any curve in one of the coordinate planes can be extended to become a surface.
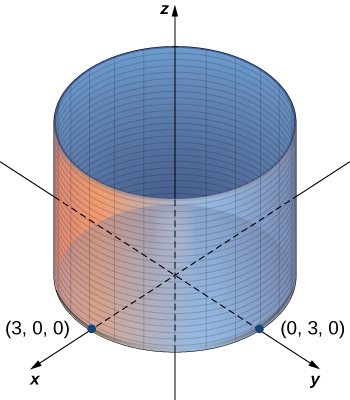
Figure 1. In three-dimensional space, the graph of equation [latex]x^{2}+y^{2}=9[/latex] is a cylinder with radius [latex]3[/latex] centered on the [latex]z[/latex]-axis. It continues indefinitely in the positive and negative directions.
DEFINITION
A set of lines parallel to a given line passing through a given curve is known as a cylindrical surface, or cylinder. The parallel lines are called rulings.
From this definition, we can see that we still have a cylinder in three-dimensional space, even if the curve is not a circle. Any curve can form a cylinder, and the rulings that compose the cylinder may be parallel to any given line (Figure 2).
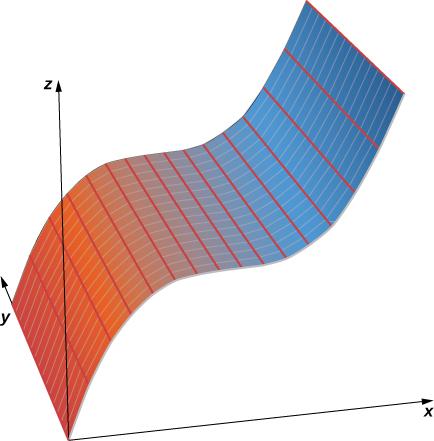
Figure 2. In three-dimensional space, the graph of equation [latex]z=x^{3}[/latex] is a cylinder, or a cylindrical surface with rulings parallel to the [latex]y[/latex]-axis.
Example: graphing cylindrical surfaces
Sketch the graphs of the following cylindrical surfaces.
- [latex]x^{2}+z^{2}=25[/latex]
- [latex]z=2x^{2}-y[/latex]
- [latex]y=\sin x[/latex]
try it
Sketch or use a graphing tool to view the graph of the cylindrical surface defined by equation [latex]z=y^{2}[/latex].
Watch the following video to see the worked solution to the above Try IT.
DEFINITION
The traces of a surface are the cross-sections created when the surface intersects a plane parallel to one of the coordinate planes.
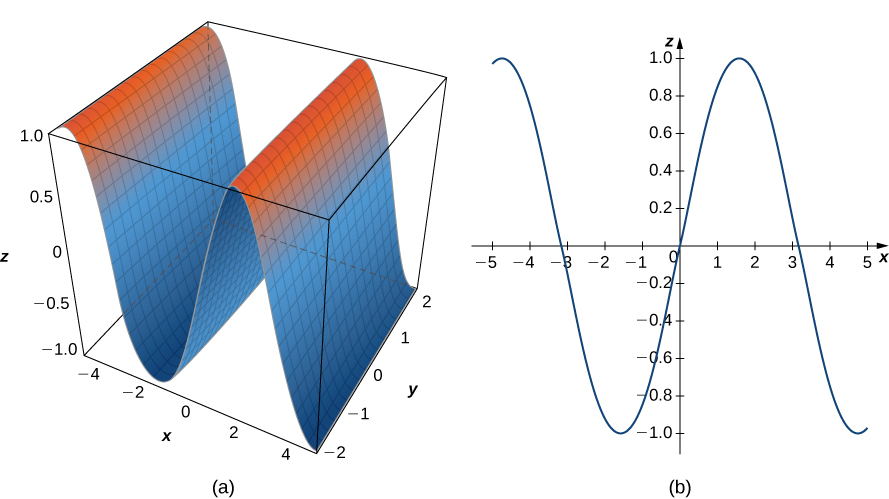
Figure 7. (a) This is one view of the graph of equation [latex]z=\sin x[/latex]. (b) To find the trace of the graph in the [latex]xz[/latex]-plane, set [latex]y=0[/latex]. The trace is simply a two-dimensional sine wave.
Traces are useful in sketching cylindrical surfaces. For a cylinder in three dimensions, though, only one set of traces is useful. Notice, in Figure 7, that the trace of the graph of [latex]z=\sin x[/latex] in the [latex]xz[/latex]-plane is useful in constructing the graph. The trace in the [latex]xy[/latex]-plane, though, is just a series of parallel lines, and the trace in the [latex]yz[/latex]-plane is simply one line.
Cylindrical surfaces are formed by a set of parallel lines. Not all surfaces in three dimensions are constructed so simply, however. We now explore more complex surfaces, and traces are an important tool in this investigation.
Candela Citations
- CP 2.52. Authored by: Ryan Melton. License: CC BY: Attribution
- Calculus Volume 3. Authored by: Gilbert Strang, Edwin (Jed) Herman. Provided by: OpenStax. Located at: https://openstax.org/books/calculus-volume-3/pages/1-introduction. License: CC BY-NC-SA: Attribution-NonCommercial-ShareAlike. License Terms: Access for free at https://openstax.org/books/calculus-volume-3/pages/1-introduction




