Equations for a Plane in Space

Learning Objectives

  • Write the vector and scalar equations of a plane through a given point with a given normal.
  • Find the distance from a point to a given plane.
  • Find the angle between two planes.

Equations for a Plane

We know that a line is determined by two points. In other words, for any two distinct points, there is exactly one line that passes through those points, whether in two dimensions or three. Similarly, given any three points that do not all lie on the same line, there is a unique plane that passes through these points. Just as a line is determined by two points, a plane is determined by three.

This may be the simplest way to characterize a plane, but we can use other descriptions as well. For example, given two distinct, intersecting lines, there is exactly one plane containing both lines. A plane is also determined by a line and any point that does not lie on the line. These characterizations arise naturally from the idea that a plane is determined by three points. Perhaps the most surprising characterization of a plane is actually the most useful.

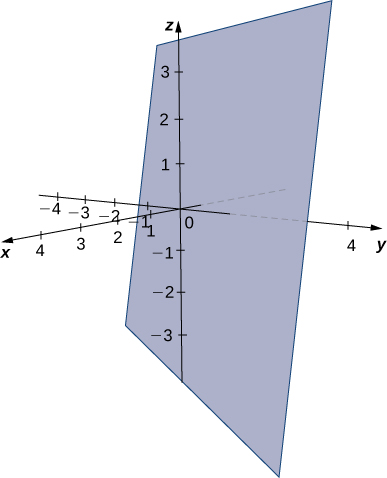
Imagine a pair of orthogonal vectors that share an initial point. Visualize grabbing one of the vectors and twisting it. As you twist, the other vector spins around and sweeps out a plane. Here, we describe that concept mathematically. Let [latex]{\bf{n}}=\langle a,b,c\rangle[/latex] be a vector and [latex]P=(x_0, y_0, z_0)[/latex] be a point. Then the set of all points [latex]Q=(x, y, z)[/latex] such that [latex]\overrightarrow{PQ}[/latex] is orthogonal to [latex]\textbf n[/latex] forms a plane (Figure 1). We say that [latex]\textbf n[/latex] is a normal vector, or perpendicular to the plane. Remember, the dot product of orthogonal vectors is zero. This fact generates the vector equation of a plane: [latex]{\bf{n}}\cdot\overrightarrow{PQ}=0[/latex]. Rewriting this equation provides additional ways to describe the plane:

[latex]\begin{aligned} {\bf{n}}\cdot\overrightarrow{PQ}&=0 \\ \langle a,b,c\rangle\cdot\langle x-x_0,y-y_0,z-z_0\rangle&=0 \\ a(x-x_0)+b(y-y_0)+c(z-z_0)&=0. \end{aligned}[/latex]

This figure is a parallelogram representing a plane. In the plane is a vector from point P to point Q. Perpendicular to the vector P Q is the vector n.

Figure 1. Given a point [latex]P[/latex] and vector [latex]\textbf n[/latex], the set of all points [latex]Q[/latex] with [latex]\overrightarrow{PQ}[/latex] orthogonal to [latex]\textbf n[/latex] forms a plane.

DEFINITION

Given a point [latex]P[/latex] and vector [latex]\textbf n[/latex], the set of all points [latex]Q[/latex] satisfying the equation [latex]{\bf{n}}\cdot\overrightarrow{PQ}=0[/latex] forms a plane. The equation

[latex]{\bf{n}}\cdot\overrightarrow{PQ}=0[/latex].

is known as the vector equation of a plane.

The scalar equation of a plane containing point [latex]P=(x_0, y_0, z_0)[/latex] with normal vector [latex]{\bf{n}}=\langle a,b,c\rangle[/latex] is

[latex]a(x-x_0)+b(y-y_0)+c(z-z_0)=0[/latex].

This equation can be expressed as [latex]ax+by+cz+d=0[/latex], where [latex]d=-ax_0-by_0-cz_0[/latex]. This form of the equation is sometimes called the general form of the equation of a plane.

As described earlier in this section, any three points that do not all lie on the same line determine a plane. Given three such points, we can find an equation for the plane containing these points.

Example: writing an equation of a plane given three points in the plane

Write an equation for the plane containing points [latex]P=(1,1,-2)[/latex], [latex]Q=(0,2,1)[/latex], and [latex]R=(-1,-1,0)[/latex] in both standard and general forms.

The scalar equations of a plane vary depending on the normal vector and point chosen.

Example: writing an equation for a plane given a point and a line

Find an equation of the plane that passes through point [latex](1, 4, 3)[/latex] and contains the line given by [latex]x=\frac{y-1}2=z+1[/latex].

try it

Find an equation of the plane containing the lines [latex]L_1[/latex] and [latex]L_2[/latex]:

[latex]L_1[/latex]: [latex]x=-y=z[/latex]

[latex]L_2[/latex]: [latex]\frac{x-3}2=y=z-2[/latex]

Watch the following video to see the worked solution to the above Try IT.

You can view the transcript for “CP 2.47” here (opens in new window).

Try It

Now that we can write an equation for a plane, we can use the equation to find the distance [latex]d[/latex] between a point [latex]P[/latex] and the plane. It is defined as the shortest possible distance from [latex]P[/latex] to a point on the plane.

This figure is the sketch of a parallelogram representing a plane. In the plane are points Q and R. there is a broken line from Q to R on the plane. There is a vector n out of the plane at point Q. Also, there is a vector labeled “R P” from point R to point P which is above the plane. This vector is perpendicular to the plane.

Figure 3. We want to find the shortest distance from point [latex]P[/latex] to the plane. Let point [latex]R[/latex] be the point in the plane such that, for any other point in the plane [latex]Q[/latex], [latex]||\overrightarrow{RP}||<||\overrightarrow{QP}||[/latex].

Just as we find the two-dimensional distance between a point and a line by calculating the length of a line segment perpendicular to the line, we find the three-dimensional distance between a point and a plane by calculating the length of a line segment perpendicular to the plane. Let [latex]R[/latex] be the point in the plane such that [latex]\overrightarrow{RP}[/latex] is orthogonal to the plane, and let [latex]Q[/latex] be an arbitrary point in the plane. Then the projection of vector [latex]\overrightarrow{QP}[/latex] onto the normal vector describes vector [latex]\overrightarrow{RP}[/latex], as shown in Figure 3.

THEOREM: the distance between a plane and a point

Suppose a plane with normal vector [latex]\textbf n[/latex] passes through point [latex]Q[/latex]. The distance [latex]d[/latex] from the plane to a point [latex]P[/latex] not in the plane is given by

[latex]d=\left|\left|\text{proj}_{\bf{n}}\overrightarrow{QP}\right|\right|=\left|\text{comp}_{\bf{n}}\overrightarrow{QP}\right|=\frac{|\overrightarrow{QP}\cdot{\bf{n}}|}{||{\bf{n}}||}[/latex].

Example: distance between a point and a plane

Find the distance between point [latex]P=(3, 1, 2)[/latex] and the plane given by [latex]x-2y+z=5[/latex] (see the following figure).

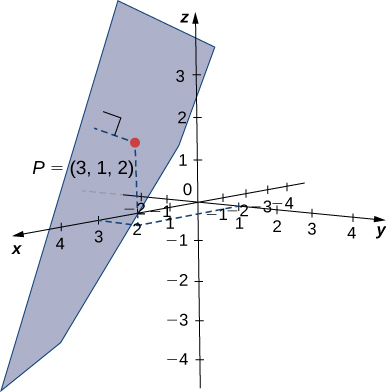
This figure is the 3-dimensional coordinate system. There is a point drawn at (3, 1, 2). The point is labeled “P(3, 1, 2).” There is a plane drawn. There is a perpendicular line from the plane to point P(3, 1, 2).

Figure 4. The distance between the plane given by [latex]x-2y+z=5[/latex] and the point [latex]P=(3, 1, 2)[/latex]

try it

Find the distance between point [latex]P=(5, -1, 0)[/latex] and the plane given by [latex]4x+2y-z=3[/latex].

Parallel and Intersecting Planes

We have discussed the various possible relationships between two lines in two dimensions and three dimensions. When we describe the relationship between two planes in space, we have only two possibilities: the two distinct planes are parallel or they intersect. When two planes are parallel, their normal vectors are parallel. When two planes intersect, the intersection is a line (Figure 5).

This figure is two planes that are intersecting. The intersection forms a line segment.

Figure 5. The intersection of two nonparallel planes is always a line.

We can use the equations of the two planes to find parametric equations for the line of intersection.

Example: finding the line of intersection for two planes

Find parametric and symmetric equations for the line formed by the intersection of the planes given by [latex]x+y+z=0[/latex] and [latex]2x-y+z=0[/latex] (see the following figure).

This figure is two planes intersecting in the 3-dimensional coordinate system.

Figure 6. The line formed by the intersection of the planes given by [latex]x+y+z=0[/latex] and [latex]2x-y+z=0[/latex]

try it

Find parametric equations for the line formed by the intersection of planes [latex]x+y-z=3[/latex] and [latex]3x-y+3z=5[/latex].

Watch the following video to see the worked solution to the above Try IT.

You can view the transcript for “CP 2.49” here (opens in new window).

In addition to finding the equation of the line of intersection between two planes, we may need to find the angle formed by the intersection of two planes. For example, builders constructing a house need to know the angle where different sections of the roof meet to know whether the roof will look good and drain properly. We can use normal vectors to calculate the angle between the two planes. We can do this because the angle between the normal vectors is the same as the angle between the planes. Figure 7 shows why this is true.

This figure is two parallelograms representing planes. The planes intersect forming angle theta between them. The first plane as vector “n sub 1” normal to the plane. The second vector has vector “n sub 2” normal to the plane. The normal vectors intersect and form the angle theta.

Figure 7. The angle between two planes has the same measure as the angle between the normal vectors for the planes.

We can find the measure of the angle [latex]\theta[/latex] between two intersecting planes by first finding the cosine of the angle, using the following equation:

[latex]\large{\cos\theta=\frac{|{\bf{n}}_1\cdot{\bf{n}}_2|}{||{\bf{n}}_1|| \ ||{\bf{n}}_2||}}[/latex].

We can then use the angle to determine whether two planes are parallel or orthogonal or if they intersect at some other angle.

Example: finding the angle between two planes

Determine whether each pair of planes is parallel, orthogonal, or neither. If the planes are intersecting, but not orthogonal, find the measure of the angle between them. Give the answer in radians and round to two decimal places.

  1. [latex]x+2y-z=8[/latex] and [latex]2x+4y-2z=10[/latex]
  2. [latex]2x-3y+2z=3[/latex] and [latex]6x+2y-3z=1[/latex]
  3. [latex]x+y+z=4[/latex] and [latex]x-3y+5z=1[/latex]

try it

Find the measure of the angle between planes [latex]x+y-z=3[/latex] and [latex]3x-y+3z=5[/latex]. Give the answer in radians and round to two decimal places.

When we find that two planes are parallel, we may need to find the distance between them. To find this distance, we simply select a point in one of the planes. The distance from this point to the other plane is the distance between the planes.

Previously, we introduced the formula for calculating this distance in The Distance between a Plane and a Point:

[latex]\large{d=\frac{\overrightarrow{QP}\cdot{\bf{n}}}{||{\bf{n}}||}}[/latex],

where [latex]Q[/latex] is a point on the plane, [latex]P[/latex] is a point not on the plane, and [latex]\textbf n[/latex] is the normal vector that passes through point [latex]Q[/latex]. Consider the distance from point [latex](x_0, y_0, z_0)[/latex] to plane [latex]ax+by+cz+k=0[/latex]. Let [latex](x_1, y_1, z_1)[/latex] be any point in the plane. Substituting into the formula yields

[latex]\large{\begin{aligned} d&=\frac{|a(x_0-x_1)+b(y_0-y_1)+c(z_0-z_1)|}{\sqrt{a^2+b^2+c^2}} \\ &=\frac{|ax_0+by_0+cz_0+k|}{\sqrt{a^2+b^2+c^2}} \end{aligned}}[/latex].

We state this result formally in the following theorem.

THEOREM: distance from a point to a plane

Let [latex]P(x_0, y_0, z_0)[/latex] be a point. The distance from [latex]P[/latex] to plane [latex]ax+by+cz+k=0[/latex] is given by

[latex]\large{d=\frac{|ax_0+by_0+cz_0+k|}{\sqrt{a^2+b^2+c^2}}}[/latex].

Example: finding the distance between parallel planes

Find the distance between the two parallel planes given by [latex]2x+y-z=2[/latex] and [latex]2x+y-z=8[/latex].

try it

Find the distance between parallel planes [latex]5x-2y+z=6[/latex] and [latex]5x-2y+z=-3[/latex].

Activity: distance between two skew lines

This figure shows a system of pipes running in different directions in an industrial plant. Two skew pipes are highlighted in red.

Figure 8. Industrial pipe installations often feature pipes running in different directions. How can we find the distance between two skew pipes?

Finding the distance from a point to a line or from a line to a plane seems like a pretty abstract procedure. But, if the lines represent pipes in a chemical plant or tubes in an oil refinery or roads at an intersection of highways, confirming that the distance between them meets specifications can be both important and awkward to measure. One way is to model the two pipes as lines, using the techniques in this chapter, and then calculate the distance between them. The calculation involves forming vectors along the directions of the lines and using both the cross product and the dot product.

The symmetric forms of two lines, [latex]L_1[/latex] and [latex]L_2[/latex], are

[latex]L_1[/latex]: [latex]\frac{x-x_1}{a_1}=\frac{y-y_1}{b_1}=\frac{z-z_1}{c_1}[/latex]

[latex]L_2[/latex]: [latex]\frac{x-x_2}{a_2}=\frac{y-y_2}{b_2}=\frac{z-z_2}{c_2}[/latex].

You are to develop a formula for the distance [latex]d[/latex] between these two lines, in terms of the values [latex]a_1[/latex], [latex]b_1[/latex], [latex]c_1[/latex]; [latex]a_2[/latex], [latex]b_2[/latex], [latex]c_2[/latex]; [latex]x_1[/latex], [latex]y_1[/latex], [latex]z_1[/latex]; and [latex]x_2[/latex], [latex]y_2[/latex], [latex]z_2[/latex]. The distance between two lines is usually taken to mean the minimum distance, so this is the length of a line segment or the length of a vector that is perpendicular to both lines and intersects both lines.

  1. First, write down two vectors, [latex]{\bf{v}}_1[/latex] and [latex]{\bf{v}}_2[/latex], that lie along [latex]L_1[/latex] and [latex]L_2[/latex], respectively.
  2. Find the cross product of these two vectors and call it [latex]\textbf N[/latex]. This vector is perpendicular to [latex]{\bf{v}}_1[/latex] and [latex]{\bf{v}}_2[/latex], and hence is perpendicular to both lines.
  3. From vector [latex]\textbf N[/latex], form a unit vector [latex]\textbf n[/latex] in the same direction.
  4. Use symmetric equations to find a convenient vector [latex]{\bf{v}}_{12}[/latex] that lies between any two points, one on each line. Again, this can be done directly from the symmetric equations.
  5. The dot product of two vectors is the magnitude of the projection of one vector onto the other—that is, [latex]{\bf{A}}\cdot{\bf{B}}=||{\bf{A}}|| \ ||{\bf{B}}||\cos\theta[/latex], where [latex]\theta[/latex] is the angle between the vectors. Using the dot product, find the projection of vector [latex]{\bf{v}}_{12}[/latex] found in step 4 onto unit vector [latex]\textbf n[/latex] found in step 3. This projection is perpendicular to both lines, and hence its length must be the perpendicular distance [latex]d[/latex] between them. Note that the value of [latex]d[/latex] may be negative, depending on your choice of vector [latex]{\bf{v}}_{12}[/latex] or the order of the cross product, so use absolute value signs around the numerator.
  6. Check that your formula gives the correct distance of [latex]|-25|/\sqrt{198}\approx1.78[/latex] between the following two lines:

    [latex]\begin{aligned} L_1&:\frac{x-5}2=\frac{y-3}4=\frac{z-1}3 \\ L_2&:\frac{x-6}3=\frac{y-1}5=\frac{z}7. \end{aligned}[/latex]

  7. Is your general expression valid when the lines are parallel? If not, why not? (Hint: What do you know about the value of the cross product of two parallel vectors? Where would that result show up in your expression for [latex]d[/latex]?)
  8. Demonstrate that your expression for the distance is zero when the lines intersect. Recall that two lines intersect if they are not parallel and they are in the same plane. Hence, consider the direction of [latex]\textbf n[/latex] and [latex]{\bf{v}}_{12}[/latex]. What is the result of their dot product?
  9. Consider the following application. Engineers at a refinery have determined they need to install support struts between many of the gas pipes to reduce damaging vibrations. To minimize cost, they plan to install these struts at the closest points between adjacent skewed pipes. Because they have detailed schematics of the structure, they are able to determine the correct lengths of the struts needed, and hence manufacture and distribute them to the installation crews without spending valuable time making measurements.
    The rectangular frame structure has the dimensions [latex]4.0\times15.0\times10.0\text{ m}[/latex] (height, width, and depth). One sector has a pipe entering the lower corner of the standard frame unit and exiting at the diametrically opposed corner (the one farthest away at the top); call this [latex]L_1[/latex]. A second pipe enters and exits at the two different opposite lower corners; call this [latex]L_2[/latex] (Figure 9).

    This figure is a three-dimensional box in an x y z coordinate system. The box has dimensions x = 10 m, y = 15 m, and z = 4 m. Line L1 passes through a main diagonal of the box from the origin to the far corner. Line L2 passes through a diagonal in the base of the box with x-intercept 10 and y-intercept 15.

    Figure 9. Two pipes cross through a standard frame unit.


    Write down the vectors along the lines representing those pipes, find the cross product between them from which to create the unit vector [latex]\textbf n[/latex], define a vector that spans two points on each line, and finally determine the minimum distance between the lines. (Take the origin to be at the lower corner of the first pipe.) Similarly, you may also develop the symmetric equations for each line and substitute directly into your formula.