Learning Outcomes
- State the conditions for continuity of a function of two variables.
- Verify the continuity of a function of two variables at a point.
- Calculate the limit of a function of three or more variables and verify the continuity of the function at a point.
In Continuity, we defined the continuity of a function of one variable and saw how it relied on the limit of a function of one variable. In particular, three conditions are necessary for [latex]f\,(x)[/latex] to be continuous at point [latex]x=a[/latex]:
- [latex]f\,(a)[/latex] exists.
- [latex]\displaystyle{\lim_{x\to{a}}}f\,(x)[/latex] exists.
- [latex]\displaystyle{\lim_{x\to{a}}}f\,(x)=f\,(a)[/latex].
These three conditions are necessary for continuity of a function of two variables as well.
Definition
A function [latex]f\,(x,\ y)[/latex] is continuous at a point [latex](a,\ b)[/latex] in its domain if the following conditions are satisfied:
- [latex]f\,(a,\ b)[/latex] exists.
- [latex]\displaystyle{\lim_{(x,\ y)\to{(a,\ b)}}}f\,(x,\ y)[/latex] exists.
- [latex]\displaystyle{\lim_{(x,\ y)\to(a,\ b)}}f\,(x,\ y)=f\,(a,\ b)[/latex].
Example: Demonstrating Continuity for a Function of Two Variables
Show that the function [latex]f\,(x,\ y)=\frac{3x+2y}{x+y+1}[/latex] is continuous at point [latex](5,-3)[/latex].
Try it
Show that the function [latex]f\,(x,y)=\sqrt{26-2x^{2}-y^{2}}[/latex] is continuous at point [latex](2,-3)[/latex].
Continuity of a function of any number of variables can also be defined in terms of delta and epsilon. A function of two variables is continuous at a point [latex](x_0,y_0)[/latex] in its domain for every [latex]\epsilon>0[/latex] there exists a [latex]\delta>0[/latex] such that, whenever [latex]\sqrt{(x-x_0)^2+(y-y_0)^2}<\delta[/latex] it is true, [latex]|f(x,y)-f(a,b)|<\epsilon[/latex]. This definition can be combined with the formal definition (that is, the epsilon-delta definition) of continuity of a function of one variable to prove the following theorems:
the sum of continuous functions is continuous
If [latex]f(x,y)[/latex] is continuous at [latex](x_0,y_0)[/latex], and [latex]g(x,y)[/latex] is continuous at [latex](x_0,y_0)[/latex], then [latex]f(x,y)+g(x,y)[/latex] is continuous at [latex](x_0,y_0)[/latex].
the product of continuous functions is continuous
If [latex]g(x)[/latex] is continuous at [latex]x_0[/latex], and [latex]h(y)[/latex] is continuous at [latex]y_0[/latex], then [latex]f(x,y)=g(x)h(y)[/latex] is continuous at [latex](x_0,y_0)[/latex].
the composition of continuous functions is continuous
Let [latex]g[/latex] be a function of two variables from a domain [latex]D\subseteq\mathbb{R}^{2}[/latex] to a range [latex]R\subseteq\mathbb{R}[/latex]. Suppose [latex]g[/latex] is continuous at some point [latex](x_0,y_0)\in{D}[/latex] and define [latex]z_0=g(x_0,y_0)[/latex]. Let [latex]f[/latex] be a function that maps [latex]\mathbb{R}[/latex] to [latex]\mathbb{R}[/latex] such that [latex]z_0[/latex] is in the domain of [latex]f[/latex]. Last, assume [latex]f[/latex] is continuous at [latex]z_0[/latex]. Then [latex]f\circ{g}[/latex] is continuous at [latex](x_0,y_0)[/latex] as shown in the following figure.
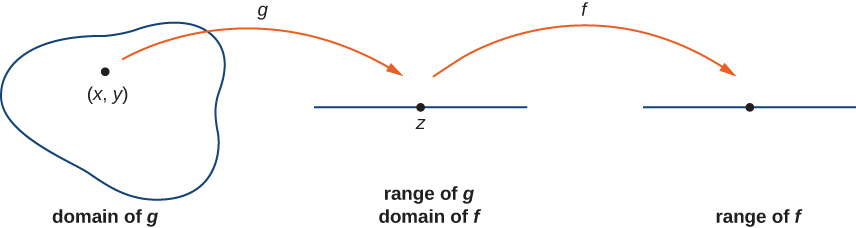
Figure 1. The composition of two continuous functions is continuous.
Let’s now use the previous theorems to show continuity of functions in the following examples.
Example: More Examples of Continuity of a Function of Two Variables
Show that the functions [latex]f\,(x,\ y)=4x^{3}y^{2}[/latex] and [latex]g\,(x,\ y)=\cos{(4x^{3}y^{2})}[/latex] are continuous everywhere.
Try it
Show that the functions [latex]f\,(x,\ y)=2x^{2}y^{3}+3[/latex] and [latex]g\,(x,\ y)=(2x^{2}y^{3}+3)^{4}[/latex] are continuous everywhere.
Watch the following video to see the worked solution to the above Try It
Functions of Three or More Variables
The limit of a function of three or more variables occurs readily in applications. For example, suppose we have a function [latex]f\,(x,\ y,\ z)[/latex] that gives the temperature at a physical location [latex](x,\ y,\ z)[/latex] in three dimensions. Or perhaps a function [latex]g\,(x,\ y,\ z,\ t)[/latex] can indicate air pressure at a location [latex](x,\ y,\ z)[/latex] at time [latex]t[/latex]. How can we take a limit at a point in [latex]\mathbb{R}^{3}[/latex]? What does it mean to be continuous at a point in four dimensions?
The answers to these questions rely on extending the concept of a [latex]\delta[/latex] disk into more than two dimensions. Then, the ideas of the limit of a function of three or more variables and the continuity of a function of three or more variables are very similar to the definitions given earlier for a function of two variables.
Definition
Let [latex](x_0,\ y_0,\ z_0)[/latex] be a point in [latex]\mathbb{R}^{3}[/latex]. Then, a [latex]\delta[/latex] ball in three dimensions consists of all points in [latex]\mathbb{R}^{3}[/latex] lying at a distance of less than [latex]\delta[/latex] from [latex](x_0,\ y_0,\ z_0)[/latex] – that is,
To define a [latex]\delta[/latex] ball in higher dimensions, add additional terms under the radical to correspond to each additional dimension. For example, given a point [latex]P=(w_0,\ x_0,\ y_0,\ z_0)[/latex] in [latex]\mathbb{R}^{4}[/latex], a [latex]\delta[/latex] ball around [latex]P[/latex] can be described by
To show that a limit of a function of three variables exists at a point [latex](x_0,\ y_0,\ z_0)[/latex], it suffices to show that for any point in a [latex]\delta[/latex] ball centered at [latex](x_0,\ y_0,\ z_0)[/latex], the value of the function at that point is arbitrarily close to a fixed value (the limit value). All the limit laws for functions of two variables hold for functions of more than two variables as well.
Example: Finding the Limit of a Function of Three Variables
Find [latex]\displaystyle\lim_{(x,\ y,\ z)\to(4,\ 1,\ -3)}\frac{x^{2}y-3z}{2x+5y-z}.[/latex]
Try it
Find [latex]\displaystyle\lim_{(x,\ y,\ z)\to(4,\ -1,\ 3)}\sqrt{13-x^{2}-2y^{2}+z^{2}}[/latex].
