Curvature

Learning Outcomes

Explain the meaning of the curvature of a curve in space and state its formula.

An important topic related to arc length is curvature. The concept of curvature provides a way to measure how sharply a smooth curve turns. A circle has constant curvature. The smaller the radius of the circle, the greater the curvature.

Think of driving down a road. Suppose the road lies on an arc of a large circle. In this case you would barely have to turn the wheel to stay on the road. Now suppose the radius is smaller. In this case you would need to turn more sharply to stay on the road. In the case of a curve other than a circle, it is often useful first to inscribe a circle to the curve at a given point so that it is tangent to the curve at that point and “hugs” the curve as closely as possible in a neighborhood of the point (Figure 1). The curvature of the graph at that point is then defined to be the same as the curvature of the inscribed circle.

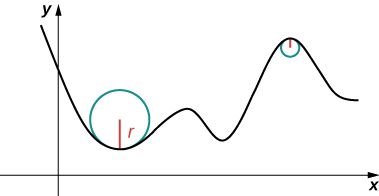
This figure is the graph of a curve. The curve rises and falls in the first quadrant. Along the curve, where the curve changes from decreasing to increasing there is a circle. The bottom of the circle curves the same as the graph of the curve. There is also a second smaller circle where the curve goes from increasing to decreasing. Part of the circle falls on the curve. Both circles have the radius r represented.

Figure 1. The graph represents the curvature of a function $y=f(x)$ . The sharper the turn in the graph, the greater the curvature, and the smaller the radius of the inscribed circle.

Definition

Let $C$ be a smooth curve in the plane or in space given by ${\bf{r}}\,(s)$ , where $s$ is the arc-length parameter. The curvature $\kappa$ at $s$ is

κ = ∥ ∥ \frac{d T}{d s} ∥ ∥ = ∥ ∥ T^{'} (s) ∥ ∥

$\LARGE{\kappa=\left\Vert\frac{d{\bf{T}}}{ds}\right\Vert=\left\Vert{\bf{T}}'\,(s)\right\Vert}$ .

Interactive

Visit this website for more information about the curvature of a space curve.

The formula in the definition of curvature is not very useful in terms of calculation. In particular, recall that ${\bf{T}}\,(t)$ represents the unit tangent vector to a given vector-valued function ${\bf{r}}\,(t)$ , and the formula ${\bf{T}}\,(t)$ is ${\bf{T}}\,(t)=\frac{{\bf{r}}'\,(t)}{\left\Vert{\bf{r}}'\,(t)\right\Vert}$ . To use the formula for curvature, it is first necessary to express ${\bf{r}}\,(t)$ in terms of the arc-length parameter $s$ , then find the unit tangent vector ${\bf{T}}\,(s)$ for the function ${\bf{r}}\,(s)$ , then take the derivative of ${\bf{T}}\,(s)$ with respect to $s$ . This is a tedious process. Fortunately, there are equivalent formulas for curvature.

Alternative formulas for curvature Theorem

If $C$ is a smooth curve given by ${\bf{r}}\,(t)$ , then the curvature $\kappa$ of $C$ at $t$ is given by

κ = \frac{∥ ∥ T^{'} (t) ∥ ∥}{∥ r^{'} (t) ∥}

$\LARGE{\kappa=\frac{\left\Vert{\bf{T}}'\,(t)\right\Vert}{\left\Vert{\bf{r}}'\,(t)\right\Vert}}$ .

If $C$ is a three-dimensional curve, then the curvature can be given by the formula

κ = \frac{∥ r^{'} (t) \times r^{''} (t) ∥}{{∥ r^{'} (t) ∥}^{3}}

$\LARGE{\kappa=\frac{\left\Vert{\bf{r}}'\,(t)\,\times\,{\bf{r}}''\,(t)\right\Vert}{\left\Vert{\bf{r}}'\,(t)\right\Vert^{3}}}$ .

If $C$ is the graph of a function $y=f\,(x)$ and both $y'$ and $y''$ exist, then the curvature $\kappa$ at point $(x,\ y)$ is given by

κ = \frac{| y^{''} |}{[1 + (y^{'})^{2}]^{3 / 2}}

$\LARGE{\kappa=\frac{|y''|}{[1+(y')^{2}]^{3/2}}}$ .

Proof

The first formula follows directly from the chain rule:

$\large{\frac{d{\bf{T}}}{dt}=\frac{d{\bf{T}}}{ds}\,\frac{ds}{dt}}$ ,

where $s$ is the arc length along the curve $C$ . Dividing both sides by $ds/dt$ , and taking the magnitude of both sides gives

$\large{\left\Vert\frac{d{\bf{T}}}{dt}\right\Vert=\left\Vert\frac{{\bf{T}}'\,(t)}{\frac{ds}{dt}}\right\Vert}$ .

Since $ds/dt=\left\Vert{\bf{r}}'\,(t)\right\Vert$ , this gives the formula for the curvature $\kappa$ of a curve $C$ in terms of any parameterization of $C$ :

$\large{\kappa=\frac{\left\Vert{\bf{T}}'\,(t)\right\Vert}{\left\Vert{\bf{r}}'\,(t)\right\Vert}}$ .

In the case of a three-dimensional curve, we start with the formulas ${\bf{T}}\,(t)=\big({\bf{r}}'\,(t)\big)/\left\Vert{\bf{r}}'\,(t)\right\Vert$ and $ds/dt=\left\Vert{\bf{r}}'\,(t)\right\Vert$ . Therefore, ${\bf{r}}'\,(t)=(ds/dt)\ {\bf{T}}\,(t)$ . We can take the derivative of this function using the scalar product formula:

${\bf{r}}''\,(t)=\frac{d^{2}s}{dt^{2}}\,{\bf{T}}\,(t)+\frac{ds}{dt}\,{\bf{T}}'\,(t)$ .

Using these last two equations we get

$\begin{array}{ccc}\hfill {{\bf{r}}'\,(t)\,\times\,{\bf{r}}''\,(t)} &=\hfill&{\frac{ds}{dt}\,{\bf{T}}\,(t)\,\times\,\big(\frac{d^{2}s}{dt^{2}}\,{\bf{T}}\,(t)+\frac{ds}{dt}\,{\bf{T}}'\,(t)\big)} \hfill \\ \hfill & =\hfill & {\frac{ds}{dt}\,\frac{d^{2}s}{dt^{2}}\,{\bf{T}}\,(t)\,\times\,{\bf{T}}\,(t)+(\frac{ds}{dt})^{2}\,{\bf{T}}\,(t)\,\times\,{\bf{T}}'\,(t).}\hfill \\ \hfill \end{array}$

Since ${\bf{T}}\,(t)\,\times\,{\bf{T}}\,(t)=0$ , this reduces to

${\bf{r}}'\,(t)\,\times\,{\bf{r}}''\,(t)=\big(\frac{ds}{dt}\big)^{2}\,{\bf{T}}\,(t)\,\times\,{\bf{T}}'\,(t)$ .

Since ${\bf{T}}'$ is parallel to ${\bf{N}}$ , and ${\bf{T}}$ is orthogonal to ${\bf{N}}$ , it follows that ${\bf{T}}$ and ${\bf{T}}'$ are orthogonal. This means that $\left\Vert{\bf{T}}\,\times\,{\bf{T}}'\right\Vert=\left\Vert{\bf{T}}\right\Vert\,\left\Vert{\bf{T}}'\right\Vert\sin{(\pi/2)}=\left\Vert{\bf{T}}'\right\Vert$ , so

$\large{\left\Vert{\bf{r}}'\,(t)\,\times\,{\bf{r}}''\,(t)\right\Vert=\big(\frac{ds}{dt}\big)\,\left\Vert{\bf{T}}'\,(t)\right\Vert}$ .

Now we solve this equation for $\left\Vert{\bf{T}}'\,(t)\right\Vert$ and use the fact that $ds/dt=\left\Vert{\bf{r}}'\,(t)\right\Vert$ :

$\large{\left\Vert{\bf{T}}'\,(t)\right\Vert=\frac{\left\Vert{\bf{r}}'\,(t)\,\times\,{\bf{r}}''\,(t)\right\Vert}{\left\Vert{\bf{r}}'\,(t)\right\Vert^{2}}}$

Then, we divide both sides by $\left\Vert{\bf{r}}'\,(t)\right\Vert$ . This gives

$\large{\kappa=\frac{\left\Vert{\bf{T}}'\,(t)\right\Vert}{\left\Vert{\bf{r}}'\,(t)\right\Vert}=\frac{\left\Vert{\bf{r}}'\,(t)\,\times\,{\bf{r}}''\,(t)\right\Vert}{\left\Vert{\bf{r}}'\,(t)\right\Vert^{3}}}$

This proves the second equation in our Alternative Formulas for Curvature Theorem. To prove the third equation in our Alternative Formulas for Curvature Theorem, we start with the assumption that curve $C$ is defined by the function . Then, we can define . Using the previous formula for curvature:

$\begin{array}{ccc}\hfill {{\bf{r}}'\,(t)} &=\hfill&{{\bf{i}}+f'\,(x)\,{\bf{j}}}\hfill \\ \hfill {{\bf{r}}''\,(t)} & =\hfill & {f''\,(x)\,{\bf{j}}} \hfill \\ \hfill {{\bf{r}}'\,(t)\,\times\,{\bf{r}}''\,(t)} & =\hfill & {\begin{vmatrix}{\bf{i}} & {\bf{j}} & {\bf{k}}\\1 & f'\,(x) & 0\\0 & f''\,(x) & 0\end{vmatrix}=f''\,(x)\,{\bf{k}}.}\hfill \\ \hfill \end{array}$

Therefore,

$\large{\kappa=\frac{\left\Vert{\bf{r}}'\,(t)\,\times\,{\bf{r}}''\,(t)\right\Vert}{\left\Vert{\bf{r}}'\,(t)\right\Vert^{3}}=\frac{|f''\,(x)|}{(1+[(f'(x))^{2}])^{3/2}}}$ .

$_\blacksquare$

Example: finding curvature

Calculate the arc length for each of the following vector-valued functions:

Show Solution

This function describes a helix.

Figure 2.

The curvature of the helix at $t=(4\pi)/3$ can be found by using the first equation from the alternative formulas curvature. First, calculate ${\bf{T}}\,(t)$ :

$\begin{array}{ccc}\hfill {{\bf{T}}\,(t)} & =\hfill & {\frac{{\bf{r}}'\,(t)}{\left\Vert{\bf{r}}'\,(t)\right\Vert}} \hfill \\ \hfill & =\hfill & {\frac{\langle{-4}\sin{t},\ 4\cos{t},\ 3\rangle}{\sqrt{(-4\sin{t})^{2}+(4\cos{t})^{2}+3^{2}}}} \hfill \\ \hfill & =\hfill & {\langle{-}\frac{4}{5}\sin{t},\ \frac{4}{5}\cos{t},\ \frac{3}{5}\rangle.} \hfill \\ \hfill \end{array}$

Next, calculate ${\bf{T}}'\,(t)$ :

$\large{{\bf{T}}'\,(t)=\langle{-}\frac{4}{5}\cos{t},\ -\frac{4}{5}\sin{t},\ 0\rangle}.$

Last, apply the first equation from the alternative formulas curvature

$\begin{array}{ccc}\hfill {\kappa} & =\hfill & {\frac{\left\Vert{\bf{T}}'\,(t)\right\Vert}{\left\Vert{\bf{r}}'\,(t)\right\Vert}=\frac{\left\Vert\langle{-}\frac{4}{5}\cos{t},\ -\frac{4}{5}\sin{t},\ 0\rangle\right\Vert}{\left\Vert\langle{-4}\sin{t},\ 4\cos{t},\ 3\rangle\right\Vert}} \hfill \\ \hfill & =\hfill & {\frac{\sqrt{(-\frac{4}{5}\cos{t})^{2}+(-\frac{4}{5}\sin{t})^{2}+0^{2}}}{\sqrt{(-4\sin{t})^{2}+(4\cos{t})^{2}+3^{2}}}} \hfill \\ \hfill & =\hfill & {\frac{4/5}{5}=\frac{4}{25}.} \hfill \\ \hfill \end{array}$

The curvature of this helix is constant at all points on the helix.
This function describes a semicircle.

Figure 3.

To find the curvature of this graph, we must use the second equation from the Alternative Formulas for Curvature. First, we calculate $y'$ and $y''$ :

$\begin{array}{ccc}\hfill {y} & =\hfill & {\sqrt{4x-x^{2}}=(4x-x^{2})^{1/2}} \hfill \\ \hfill {y'} & =\hfill & {\frac{1}{2}\,(4x-x^{2})^{-1/2}\,(4-2x)=(2-x)\,(4x-x^{2})^{-1/2}} \hfill \\ \hfill {y''} & =\hfill & {-(4x-x^{2})^{-1/2}+(2-x)\,(-\frac{1}{2})\,(4x-x^{2})^{-3/2}\,(4-2x)} \hfill \\ \hfill & =\hfill & {-\frac{4x-x^{2}}{(4x-x^{2})^{3/2}}-\frac{(2-x)^{2}}{(4x-x^{2})^{3/2}}} \hfill \\ \hfill & =\hfill & {\frac{x^{2}-4x-(4-4x+x^{2})}{(4x-x^{2})^{3/2}}} \hfill \\ \hfill & =\hfill & {-\frac{4}{(4x-x^{2})^{3/2}}.} \hfill \\ \hfill\end{array}$

Then, we apply the third equation from the Alternative Formulas for Curvature:

$\begin{array}{ccc}\hfill {\kappa} & =\hfill & {\frac{|y''|}{[1+(y')^{2}]^{3/2}}} \hfill \\ \hfill & =\hfill & {\frac{\Bigg|-\frac{4}{(4x-x^{2})^{3/2}}\Bigg|}{\bigg[1+\big((2-x)(4x-x^{2})^{-1/2}\big)^{2}\bigg]^{3/2}}=\frac{\Bigg|\frac{4}{(4x-x^{2})^{3/2}}\Bigg|}{\bigg[1+\frac{(2-x)^{2}}{4x-x^{2}}\bigg]^{3/2}}} \hfill \\ \hfill & =\hfill & {\frac{\Bigg|\frac{4}{(4x-x^{2})^{3/2}}\Bigg|}{\bigg[\frac{4x-x^{2}+x^{2}-4x+4}{4x-x^{2}}\bigg]^{3/2}}=\bigg|\frac{4}{(4x-x^{2})^{3/2}}\bigg|\cdot\frac{(4x-x^{2})^{3/2}}{8}} \hfill \\ \hfill & =\hfill & {\frac{1}{2}.} \hfill \\ \hfill\end{array}$

The curvature of this circle is equal to the reciprocal of its radius. There is a minor issue with the absolute value is the second equation from the Alternative Formulas for Curvature; however, a closer look at the calculation reveals that the denominator is positive for any value of $x$ .

try it

Find the curvature of the curve defined by the function

$y=3x^{2}-2x+4$

at the point $x=2$ .

Show Solution

$\large{\kappa=\frac{6}{101^{3/2}}\approx{0.0059}}$

Watch the following video to see the worked solution to the above Try It

You can view the transcript for “CP 3.11” here (opens in new window).

Module 3: Vector-Valued Functions