Equations for a Line in Space

Learning Objectives

  • Write the vector, parametric, and symmetric equations of a line through a given point in a given direction, and a line through two given points.
  • Find the distance from a point to a given line.

Equations for a Line in Space

Let’s first explore what it means for two vectors to be parallel. Recall that parallel vectors must have the same or opposite directions. If two nonzero vectors, [latex]\textbf u[/latex] and [latex]\textbf v[/latex], are parallel, we claim there must be a scalar, [latex]k[/latex], such that [latex]{\bf{u}}=k{\bf{v}}[/latex]. If [latex]\textbf u[/latex] and [latex]\textbf v[/latex] have the same direction, simply choose [latex]k=\frac{||{\bf{u}}||}{||{\bf{v}}||}[/latex]. If [latex]\textbf u[/latex] and [latex]\textbf v[/latex] have opposite directions, choose [latex]k=-\frac{||{\bf{u}}||}{||{\bf{v}}||}[/latex]. Note that the converse holds as well. If [latex]{\bf{u}}=k{\bf{v}}[/latex] for some scalar [latex]k[/latex], then either [latex]\textbf u[/latex] and [latex]\textbf v[/latex] have the same direction [latex](k>0)[/latex] or opposite directions [latex](k<0)[/latex], so [latex]\textbf u[/latex] and [latex]\textbf v[/latex] are parallel. Therefore, two nonzero vectors [latex]\textbf u[/latex] and [latex]\textbf v[/latex] are parallel if and only if [latex]{\bf{u}}=k{\bf{v}}[/latex] for some scalar [latex]k[/latex]. By convention, the zero vector [latex]\textbf 0[/latex] is considered to be parallel to all vectors.

As in two dimensions, we can describe a line in space using a point on the line and the direction of the line, or a parallel vector, which we call the direction vector (Figure 1). Let [latex]L[/latex] be a line in space passing through point [latex]P(x_0, y_0, z_0)[/latex]. Let [latex]{\bf{v}}=\langle a,b,c\rangle[/latex] be a vector parallel to [latex]L[/latex]. Then, for any point on line [latex]Q(x, y, z)[/latex], we know that [latex]\overrightarrow{PQ}[/latex] is parallel to [latex]\textbf v[/latex]. Thus, as we just discussed, there is a scalar, [latex]t[/latex], such that [latex]\overrightarrow{PQ}=t{\bf{v}}[/latex], which gives

[latex]\begin{aligned} \overrightarrow{PQ}&=t{\bf{v}} \\ \langle x-x_0,y-y_0,z-z_0\rangle&=t\langle a,b,c\rangle \\ \langle x-x_0,y-y_0,z-z_0\rangle&=\langle ta,tb,tc\rangle. \end{aligned}[/latex]
This figure is the first octant of the 3-dimensional coordinate system. There is a line segment passing through two points. The points are labeled “P = (x sub 0, y sub 0, z sub 0)” and “Q = (x, y, z).” There is also a vector in standard position drawn. The vector is labeled “v = <a, b, c>.”

Figure 1. Vector [latex]\textbf v[/latex] is the direction vector for [latex]\overrightarrow{PQ}[/latex].

Using vector operations, we can rewrite this equation as

[latex]\begin{aligned} \langle x-x_0,y-y_0,z-z_0\rangle&=\langle ta,tb,tc\rangle \\ \langle x,y,z\rangle -\langle x_0,y_0,z_0\rangle&=t\langle a,b,c\rangle \\ \langle x,y,z\rangle&=\langle x_0,y_0,z_0\rangle+t\langle a,b,c\rangle \end{aligned}[/latex].

Setting [latex]{\bf{r}}=\langle x,y,z\rangle[/latex] and [latex]{\bf{r}}_0=\langle x_0,y_0,z_0\rangle[/latex], we now have the vector equation of a line:

[latex]{\bf{r}}={\bf{r}}_0+t{\bf{v}}[/latex].

Equating components, the Vector Equation of a Line shows that the following equations are simultaneously true: [latex]x-x_0=ta[/latex], [latex]y-y_0=tb[/latex], and [latex]z-z_0=tc[/latex]. If we solve each of these equations for the component variables [latex]x[/latex], [latex]y[/latex], and [latex]z[/latex], we get a set of equations in which each variable is defined in terms of the parameter [latex]t[/latex] and that, together, describe the line. This set of three equations forms a set of parametric equations of a line:

[latex]x=x_0+ta \quad y=y_0+tb \quad z=z_0+tc[/latex].

If we solve each of the equations for [latex]t[/latex] assuming [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] are nonzero, we get a different description of the same line:

[latex]\frac{x-x_0}a=t \quad \frac{y-y_o}b=t \quad \frac{z-z_0}c=t[/latex].

Because each expression equals [latex]t[/latex], they all have the same value. We can set them equal to each other to create symmetric equations of a line:

[latex]\frac{x-x_0}a=\frac{y-y_o}b=\frac{z-z_0}c[/latex].

We summarize the results in the following theorem.

THEOREM: parametric and symmetric equations of a line

A line [latex]L[/latex] parallel to vector [latex]{\bf{v}}=\langle a,b,c\rangle[/latex] and passing through point [latex]P(x_0, y_0, z_0)[/latex] can be described by the following parametric equations:

[latex]x=x_0+ta, \ y=y_0+tb, \ z=z_0+tc[/latex].

If the constants [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] are all nonzero, then [latex]L[/latex] can be described by the symmetric equation of the line:

[latex]\frac{x-x_0}a=\frac{y-y_o}b=\frac{z-z_0}c[/latex].

The parametric equations of a line are not unique. Using a different parallel vector or a different point on the line leads to a different, equivalent representation. Each set of parametric equations leads to a related set of symmetric equations, so it follows that a symmetric equation of a line is not unique either.

Example: equations of a line in space

Find parametric and symmetric equations of the line passing through points [latex](1, 4, -2)[/latex] and [latex](-3, 5, 0)[/latex].

try it

Find parametric and symmetric equations of the line passing through points [latex](1, -3, 2)[/latex] and [latex](5, -2 ,8)[/latex].

Sometimes we don’t want the equation of a whole line, just a line segment. In this case, we limit the values of our parameter [latex]t[/latex]. For example, let [latex]P(x_0, y_0, z_0)[/latex] and [latex]Q(x_1, y_1, z_1)[/latex] be points on a line, and let [latex]{\bf{p}}=\langle x_0,y_0,z_0\rangle[/latex] and [latex]{\bf{q}}=\langle x_1,y_1,z_1\rangle[/latex] be the associated position vectors. In addition, let [latex]{\bf{r}}=\langle x,y,z\rangle[/latex]. We want to find a vector equation for the line segment between [latex]P[/latex] and [latex]Q[/latex]. Using [latex]P[/latex] as our known point on the line, and [latex]\overrightarrow{PQ}=\langle x_1-x_0,y_1-y_0,z_1-z_0\rangle[/latex] as the direction vector equation, the Vector Equation of a Line gives

[latex]{\bf{r}}={\bf{p}}+t \left( \overrightarrow{PQ}\right)[/latex].

Using properties of vectors, then

[latex]\begin{aligned} {\bf{r}}&={\bf{p}}+ t \left(\overrightarrow{PQ}\right) \\ &=\langle x_0,y_0,z_0\rangle+t\langle x_1-x_0,y_1-y_0,z_1-z_0\rangle \\ &=\langle x_0,y_0,z_0\rangle+t(\langle x_1,y_1,z_1\rangle-\langle x_0,y_0,z_0\rangle) \\ &=\langle x_0,y_0,z_0\rangle+t\langle x_1,y_1,z_1\rangle-t\langle x_0,y_0,z_0\rangle \\ &=(1-t)\langle x_0,y_0,z_0\rangle+t\langle x_1,y_1,z_1\rangle \\ &=(1-t){\bf{p}}+t{\bf{q}} \end{aligned}[/latex].

Thus, the vector equation of the line passing through [latex]P[/latex] and [latex]Q[/latex] is

[latex]{\bf{r}}=(1-t){\bf{p}}+t{\bf{q}}[/latex].

Remember that we didn’t want the equation of the whole line, just the line segment between [latex]P[/latex] and [latex]Q[/latex]. Notice that when [latex]t=0[/latex], we have [latex]{\bf{r}}={\bf{p}}[/latex], and when [latex]t=1[/latex], we have [latex]{\bf{r}}={\bf{q}}[/latex]. Therefore, the vector equation of the line segment between [latex]P[/latex] and [latex]Q[/latex] is

[latex]{\bf{r}}=(1-t){\bf{p}}+t{\bf{q}}[/latex], [latex]0\leq t\leq1[/latex].

Going back to the Vector Equation of a Line, we can also find parametric equations for this line segment. We have

[latex]\begin{aligned} {\bf{r}}&={\bf{p}}+\left(\overrightarrow{PQ}\right) \\ \langle x,y,z\rangle &=\langle x_0,y_0,z_0\rangle+t\langle x_1-x_0,y_1-y_0,z_1-z_0\rangle \\ &=\langle x_0+t(x_1-x_0),y_0+t(y_1-y_0),z_0+t(z_1-z_0)\rangle \end{aligned}[/latex].

Then, the parametric equations are

[latex]x=x_0+t(x_1-x_0)[/latex], [latex]y=y_0+t(y_1-y_0)[/latex], [latex]z=z_0+t(z_1-z_0)[/latex], [latex]0\leq t\leq1[/latex].

Example: parametric equations of a line segment

Find parametric equations of the line segment between the points [latex]P(2, 1, 4)[/latex] and [latex]Q(3, -1 ,3)[/latex].

try it

Find parametric equations of the line segment between points [latex]P(-1, 3, 6)[/latex] and [latex]Q(-8, 2, 4)[/latex].

Distance between a Point and a Line

We already know how to calculate the distance between two points in space. We now expand this definition to describe the distance between a point and a line in space. Several real-world contexts exist when it is important to be able to calculate these distances. When building a home, for example, builders must consider “setback” requirements, when structures or fixtures have to be a certain distance from the property line. Air travel offers another example. Airlines are concerned about the distances between populated areas and proposed flight paths.

Let [latex]L[/latex] be a line in the plane and let [latex]M[/latex] be any point not on the line. Then, we define distance [latex]d[/latex] from [latex]M[/latex] to [latex]L[/latex] as the length of line segment [latex]\overline{MP}[/latex], where [latex]P[/latex] is a point on [latex]L[/latex] such that [latex]\overline{MP}[/latex] is perpendicular to [latex]L[/latex] (Figure 2).

This figure has two line segments. The first line is labeled “L” and has point P on the segment. The second line segment is drawn from point P to point M and is perpendicular to line L. The second line segment is labeled “d.”

Figure 2. The distance from point [latex]M[/latex] to line [latex]L[/latex] is the length of [latex]\overline{MP}[/latex].

When we’re looking for the distance between a line and a point in space, Figure 2 still applies. We still define the distance as the length of the perpendicular line segment connecting the point to the line. In space, however, there is no clear way to know which point on the line creates such a perpendicular line segment, so we select an arbitrary point on the line and use properties of vectors to calculate the distance. Therefore, let [latex]P[/latex] be an arbitrary point on line [latex]L[/latex] and let [latex]\textbf v[/latex] be a direction vector for [latex]L[/latex] (Figure 3).
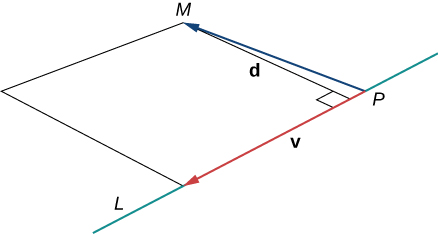
This figure has a line segment labeled “L.” On the line segment L there is point P. There is a vector drawn from point P to another point M. Also, from M there is a line segment drawn to line L. This segment is perpendicular to line L. There is also a vector labeled “v” on line segment L. A parallelogram has been formed with vector v, line segment P M, and two other segments back to line L.

Figure 3. Vectors [latex]\overrightarrow{PM}[/latex] and [latex]\textbf v[/latex] form two sides of a parallelogram with base [latex]||{\bf{v}}||[/latex] and height [latex]d[/latex], which is the distance between a line and a point in space.

By Theorem: Area of a Parallelogram, vectors [latex]\overrightarrow{PM}[/latex] and [latex]\textbf v[/latex] form two sides of a parallelogram with area [latex]||\overrightarrow{PM}\times{\bf{v}}||[/latex]. Using a formula from geometry, the area of this parallelogram can also be calculated as the product of its base and height:

[latex]||\overrightarrow{PM}\times{\bf{v}}||=||{\bf{v}}||d[/latex].

We can use this formula to find a general formula for the distance between a line in space and any point not on the line.

THEOREM: distance from a point to a line

Let [latex]L[/latex] be a line in space passing through point [latex]P[/latex] with direction vector [latex]\textbf v[/latex]. If [latex]M[/latex] is any point not on [latex]L[/latex], then the distance from [latex]M[/latex] to [latex]L[/latex] is

[latex]d=\frac{||\overrightarrow{PM}\times{\bf{v}}||}{||{\bf{v}}||}[/latex].

Example: calculating the distance from a point to a line

Find the distance between t point [latex]M=(1, 1, 3)[/latex] and line [latex]\frac{x-3}4=\frac{y+1}2=z-3[/latex].

try it

Find the distance between point [latex](0, 3, 6)[/latex] and the line with parametric equations [latex]x=1-t[/latex], [latex]y=1+2t[/latex], [latex]z=5+3t[/latex].

Watch the following video to see the worked solution to the above Try IT.

You can view the transcript for “CP 2.45” here (opens in new window).

Relationships between Lines

Given two lines in the two-dimensional plane, the lines are equal, they are parallel but not equal, or they intersect in a single point. In three dimensions, a fourth case is possible. If two lines in space are not parallel, but do not intersect, then the lines are said to be skew lines (Figure 5).

This figure has two line segments. They are 3-dimensional, are not parallel, and do not intersect. The directions are different and one is above the other.

Figure 5. In three dimensions, it is possible that two lines do not cross, even when they have different directions.

To classify lines as parallel but not equal, equal, intersecting, or skew, we need to know two things: whether the direction vectors are parallel and whether the lines share a point (Figure 6).
This figure is a table with two rows and two columns. Above the columns is the question “Lines share a common point?” The first column is labeled “yes,” and the second column is labeled “no.” To the left of the rows is the question “Direction vectors are parallel?” The first row is labeled “yes,” and the second row is labeled “no.” The entries of the first row are “equal” and “parallel but not equal.” The entries in the second row are “intersecting” and “skew.”

Figure 6. Determine the relationship between two lines based on whether their direction vectors are parallel and whether they share a point.

Example: classifying lines in space

For each pair of lines, determine whether the lines are equal, parallel but not equal, skew, or intersecting.

  1. [latex]L_1[/latex]: [latex]x=2s-1[/latex], [latex]y=s-1[/latex], [latex]z=s-4[/latex]
    [latex]L_2[/latex]: [latex]x=t-3[/latex], [latex]y=3t+8[/latex], [latex]z=5-2t[/latex]
  2. [latex]L_1[/latex]: [latex]x=-y=z[/latex]
    [latex]L_2[/latex]: [latex]\frac{x-3}2=y=z-2[/latex]
  3. [latex]L_1[/latex]: [latex]x=6s-1[/latex], [latex]y=-2s[/latex], [latex]z=3s+1[/latex]
    [latex]L_2[/latex]: [latex]\frac{x-4}6=\frac{y+3}{-2}=\frac{z-1}3[/latex]

try it

Describe the relationship between the lines with the following parametric equations:

[latex]x=1-4t[/latex], [latex]y=3+t[/latex], [latex]z=8-6t[/latex]

[latex]x=2+3s[/latex], [latex]y=2s[/latex], [latex]z=-1-3s[/latex].