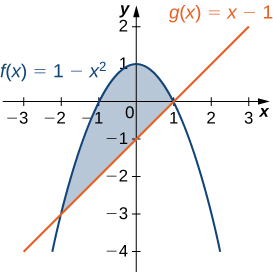In the Calculating Centers of Mass and Moments of Inertia section, we will explore how to calculate the center of mass and moment of inertia in two and three dimensions. Here we will review how to write the equation of a line and locate the center of mass of a lamina.

Write the Equation of a Line

(also in Module 1, Skills Review for Parametric Equations and Calculus of Parametric Equations)
The slope of a line refers to the ratio of the vertical change in y over the horizontal change in x between any two points on a line.

To write the equation of a line, the line’s slope and a point the line goes through must be known. Perhaps the most familiar form of a linear equation is slope-intercept form written as [latex]y=mx+b[/latex], where [latex]m=\text{slope}[/latex] and [latex]b=y\text{-intercept}[/latex]. Let us begin with the slope.

Often, the starting point to writing the equation of a line is to use point-slope formula. Given the slope and one point on a line, we can find the equation of the line using point-slope form shown below.

We need only one point and the slope of the line to use the formula. After substituting the slope and the coordinates of one point into the formula, we simplify it and write it in slope-intercept form.

Center of Mass of Thin Plates

An object that is a two-dimensional “sheet” (such as paper) is called a lamina. A lamina is often represented by a two-dimensional region in a plane. Suppose we have a lamina bounded above by the graph of a continuous function [latex]f(x),[/latex] below by the [latex]x[/latex]-axis, and on the left and right by the lines [latex]x=a[/latex] and [latex]x=b,[/latex] respectively, as shown in the following figure.

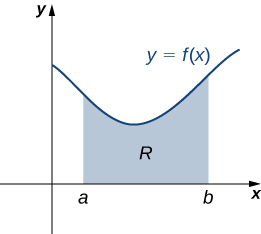
A region in the plane representing a lamina.

To find the center of mass of a lamina, we need to find the total mass of the lamina, as well as the moments of the lamina with respect to the [latex]x[/latex]– and [latex]y[/latex]-axes.

Center of Mass of a Thin Plate in the xy-Plane

---

Let R denote a region bounded above by the graph of a continuous function [latex]f(x),[/latex] below by the [latex]x[/latex]-axis, and on the left and right by the lines [latex]x=a[/latex] and [latex]x=b,[/latex] respectively. Let [latex]\rho [/latex] denote the density of the associated lamina. Then we can make the following statements:

1. The mass of the lamina is
   [latex]m=\rho {\displaystyle\int }_{a}^{b}f(x)dx.[/latex]
2. The moments [latex]{M}_{x}[/latex] and [latex]{M}_{y}[/latex] of the lamina with respect to the [latex]x[/latex]– and [latex]y[/latex]-axes, respectively, are
   [latex]{M}_{x}=\rho {\displaystyle\int }_{a}^{b}\frac{{\left[f(x)\right]}^{2}}{2}dx\text{ and }{M}_{y}=\rho {\displaystyle\int }_{a}^{b}xf(x)dx.[/latex]
3. The coordinates of the center of mass [latex](\overline{x},\overline{y})[/latex] are
   [latex]\overline{x}=\frac{{M}_{y}}{m}\text{ and }\overline{y}=\frac{{M}_{x}}{m}.[/latex]

Example: Finding the Center of Mass of a Lamina

Let R be the region bounded above by the graph of the function [latex]f(x)=\sqrt{x}[/latex] and below by the [latex]x[/latex]-axis over the interval [latex]\left[0,4\right].[/latex] Find the centroid (center of mass) of the region.

Show Solution

The region is depicted in the following figure.

Since we are only asked for the centroid of the region, rather than the mass or moments of the associated lamina, we know the density constant [latex]\rho [/latex] cancels out of the calculations eventually. Therefore, for the sake of convenience, let’s assume [latex]\rho =1.[/latex]

First, we need to calculate the total mass:

[latex]\begin{array}{cc}\hfill m& =\rho {\displaystyle\int }_{a}^{b}f(x)dx={\displaystyle\int }_{0}^{4}\sqrt{x}dx\hfill \\ & ={\frac{2}{3}{x}^{3\text{/}2}|}_{0}^{4}=\frac{2}{3}\left[8-0\right]=\frac{16}{3}.\hfill \end{array}[/latex]

Next, we compute the moments:

[latex]\begin{array}{cc}\hfill {M}_{x}& =\rho {\displaystyle\int }_{a}^{b}\frac{{\left[f(x)\right]}^{2}}{2}dx\hfill \\ & ={\displaystyle\int }_{0}^{4}\frac{x}{2}dx={\frac{1}{4}{x}^{2}|}_{0}^{4}=4\hfill \end{array}[/latex]

and

[latex]\begin{array}{cc}\hfill {M}_{y}& =\rho {\displaystyle\int }_{a}^{b}xf(x)dx\hfill \\ & ={\displaystyle\int }_{0}^{4}x\sqrt{x}dx={\displaystyle\int }_{0}^{4}{x}^{3\text{/}2}dx\hfill \\ & ={\frac{2}{5}{x}^{5\text{/}2}|}_{0}^{4}=\frac{2}{5}\left[32-0\right]=\frac{64}{5}.\hfill \end{array}[/latex]

Thus, we have

[latex]\overline{x}=\frac{{M}_{y}}{m}=\frac{64\text{/}5}{16\text{/}3}=\frac{64}{5}·\frac{3}{16}=\frac{12}{5}\text{ and }\overline{y}=\frac{{M}_{x}}{y}=\frac{4}{16\text{/}3}=4·\frac{3}{16}=\frac{3}{4}.[/latex]

The centroid of the region is [latex](12\text{/}5,3\text{/}4).[/latex]

Try It

Let [latex]R[/latex] be the region bounded above by the graph of the function [latex]f(x)={x}^{2}[/latex] and below by the [latex]x[/latex]-axis over the interval [latex]\left[0,2\right].[/latex]. Find the centroid (center of mass) of the region.

Hint

Use the process from the previous example.

Show Solution

The centroid of the region is [latex](\frac{3}{2},\frac{6}{5}).[/latex]

We can adapt this approach to find centroids of more complex regions as well. Suppose our region is bounded above by the graph of a continuous function [latex]f(x),[/latex] as before, but now, instead of having the lower bound for the region be the [latex]x[/latex]-axis, suppose the region is bounded below by the graph of a second continuous function, [latex]g(x),[/latex] as shown in the following figure.

A region between two functions.

Again, we partition the interval [latex]\left[a,b\right][/latex] and construct rectangles. A representative rectangle is shown in the following figure.

A representative rectangle of the region between two functions.

Center of Mass of a Lamina Bounded by Two Functions

---

Let R denote a region bounded above by the graph of a continuous function [latex]f(x),[/latex] below by the graph of the continuous function [latex]g(x),[/latex] and on the left and right by the lines [latex]x=a[/latex] and [latex]x=b,[/latex] respectively. Let [latex]\rho [/latex] denote the density of the associated lamina. Then we can make the following statements:

1. The mass of the lamina is
   [latex]m=\rho {\displaystyle\int }_{a}^{b}\left[f(x)-g(x)\right]dx.[/latex]
2. The moments [latex]{M}_{x}[/latex] and [latex]{M}_{y}[/latex] of the lamina with respect to the [latex]x[/latex]– and [latex]y[/latex]-axes, respectively, are
   [latex]{M}_{x}=\rho {\displaystyle\int }_{a}^{b}\frac{1}{2}({\left[f(x)\right]}^{2}-{\left[g(x)\right]}^{2})dx\text{ and }{M}_{y}=\rho {\displaystyle\int }_{a}^{b}x\left[f(x)-g(x)\right]dx.[/latex]
3. The coordinates of the center of mass [latex](\overline{x},\overline{y})[/latex] are
   [latex]\overline{x}=\frac{{M}_{y}}{m}\text{ and }\overline{y}=\frac{{M}_{x}}{m}.[/latex]

Example: Finding the Centroid of a Region Bounded by Two Functions

Let R be the region bounded above by the graph of the function [latex]f(x)=1-{x}^{2}[/latex] and below by the graph of the function [latex]g(x)=x-1.[/latex] Find the centroid of the region.

Show Solution

The region is depicted in the following figure.

Finding the centroid of a region between two curves.

The graphs of the functions intersect at [latex](-2,-3)[/latex] and [latex](1,0),[/latex] so we integrate from −2 to 1. Once again, for the sake of convenience, assume [latex]\rho =1.[/latex]

First, we need to calculate the total mass:

[latex]\begin{array}{cc}\hfill m& =\rho {\displaystyle\int }_{a}^{b}\left[f(x)-g(x)\right]dx\hfill \\ & ={\displaystyle\int }_{-2}^{1}\left[1-{x}^{2}-(x-1)\right]dx={\displaystyle\int }_{-2}^{1}(2-{x}^{2}-x)dx\hfill \\ & ={\left[2x-\frac{1}{3}{x}^{3}-\frac{1}{2}{x}^{2}\right]|}_{-2}^{1}=\left[2-\frac{1}{3}-\frac{1}{2}\right]-\left[-4+\frac{8}{3}-2\right]=\frac{9}{2}.\hfill \end{array}[/latex]

Next, we compute the moments:

[latex]\begin{array}{cc}\hfill {M}_{x}& =\rho {\displaystyle\int }_{a}^{b}\frac{1}{2}({\left[f(x)\right]}^{2}-{\left[g(x)\right]}^{2})dx\hfill \\ & =\frac{1}{2}{\displaystyle\int }_{-2}^{1}({(1-{x}^{2})}^{2}-{(x-1)}^{2})dx=\frac{1}{2}{\displaystyle\int }_{-2}^{1}({x}^{4}-3{x}^{2}+2x)dx\hfill \\ & =\frac{1}{2}{\left[\frac{{x}^{5}}{5}-{x}^{3}+{x}^{2}\right]|}_{-2}^{1}=-\frac{27}{10}\hfill \end{array}[/latex]

and

[latex]\begin{array}{cc}\hfill {M}_{y}& =\rho {\displaystyle\int }_{a}^{b}x\left[f(x)-g(x)\right]dx\hfill \\ & ={\displaystyle\int }_{-2}^{1}x\left[(1-{x}^{2})-(x-1)\right]dx={\displaystyle\int }_{-2}^{1}x\left[2-{x}^{2}-x\right]dx={\displaystyle\int }_{-2}^{1}(2x-{x}^{4}-{x}^{2})dx\hfill \\ & ={\left[{x}^{2}-\frac{{x}^{5}}{5}-\frac{{x}^{3}}{3}\right]|}_{-2}^{1}=-\frac{9}{4}.\hfill \end{array}[/latex]

Therefore, we have

[latex]\overline{x}=\frac{{M}_{y}}{m}=-\frac{9}{4}·\frac{2}{9}=-\frac{1}{2}\text{ and }\overline{y}=\frac{{M}_{x}}{y}=-\frac{27}{10}·\frac{2}{9}=-\frac{3}{5}.[/latex]

The centroid of the region is [latex](\text{−}(1\text{/}2),\text{−}(3\text{/}5)).[/latex]

Try It

Let R be the region bounded above by the graph of the function [latex]f(x)=6-{x}^{2}[/latex] and below by the graph of the function [latex]g(x)=3-2x.[/latex] Find the centroid of the region.

Hint

Use the process from the previous example.

Show Solution

The centroid of the region is [latex](1,\frac{13}{5}).[/latex]