Skills Review for Conic Sections

Learning Outcomes

  • Find the distance between two points
  • Find the midpoint of a line segment
  • Complete the square

In the Conic Section section, we will learn about various conic sections including parabolas, ellipses, and hyperbolas. Here we will review how to use both the distance and midpoint formulas along with how to complete the square.

Find the Distance Between Two Points

Derived from the Pythagorean Theorem, the distance formula is used to find the distance between two points in the plane. The Pythagorean Theorem, [latex]{a}^{2}+{b}^{2}={c}^{2}[/latex], is based on a right triangle where a and b are the lengths of the legs adjacent to the right angle, and c is the length of the hypotenuse.

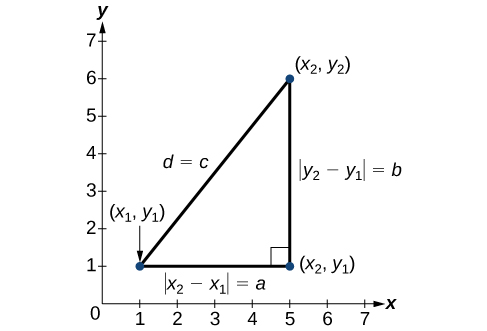
This is an image of a triangle on an x, y coordinate plane. The x and y axes range from 0 to 7. The points (x sub 1, y sub 1); (x sub 2, y sub 1); and (x sub 2, y sub 2) are labeled and connected to form a triangle. Along the base of the triangle, the following equation is displayed: the absolute value of x sub 2 minus x sub 1 equals a. The hypotenuse of the triangle is labeled: d = c. The remaining side is labeled: the absolute value of y sub 2 minus y sub 1 equals b.

The relationship of sides [latex]|{x}_{2}-{x}_{1}|[/latex] and [latex]|{y}_{2}-{y}_{1}|[/latex] to side d is the same as that of sides a and b to side c. We use the absolute value symbol to indicate that the length is a positive number because the absolute value of any number is positive. (For example, [latex]|-3|=3[/latex]. ) The symbols [latex]|{x}_{2}-{x}_{1}|[/latex] and [latex]|{y}_{2}-{y}_{1}|[/latex] indicate that the lengths of the sides of the triangle are positive. To find the length c, take the square root of both sides of the Pythagorean Theorem.

[latex]{c}^{2}={a}^{2}+{b}^{2}\rightarrow c=\sqrt{{a}^{2}+{b}^{2}}[/latex]

It follows that the distance formula is given as

[latex]{d}^{2}={\left({x}_{2}-{x}_{1}\right)}^{2}+{\left({y}_{2}-{y}_{1}\right)}^{2}\to d=\sqrt{{\left({x}_{2}-{x}_{1}\right)}^{2}+{\left({y}_{2}-{y}_{1}\right)}^{2}}[/latex]

We do not have to use the absolute value symbols in this definition because any number squared is positive.

A General Note: The Distance Formula

Given endpoints [latex]\left({x}_{1},{y}_{1}\right)[/latex] and [latex]\left({x}_{2},{y}_{2}\right)[/latex], the distance between two points is given by

[latex]d=\sqrt{{\left({x}_{2}-{x}_{1}\right)}^{2}+{\left({y}_{2}-{y}_{1}\right)}^{2}}[/latex]

Example: Finding the Distance between Two Points

Find the distance between the points [latex]\left(-3,-1\right)[/latex] and [latex]\left(2,3\right)[/latex].

Try It

Find the distance between two points: [latex]\left(1,4\right)[/latex] and [latex]\left(11,9\right)[/latex].

Find the Midpoint of a Line Segment

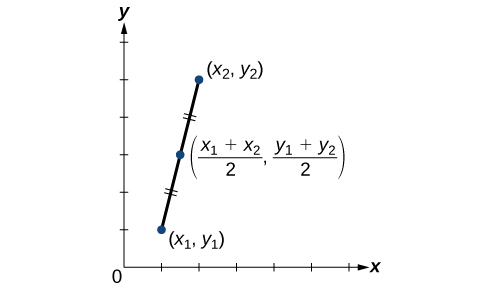
When the endpoints of a line segment are known, we can find the point midway between them. This point is known as the midpoint and the formula is known as the midpoint formula. Given the endpoints of a line segment, [latex]\left({x}_{1},{y}_{1}\right)[/latex] and [latex]\left({x}_{2},{y}_{2}\right)[/latex], the midpoint formula states how to find the coordinates of the midpoint [latex]M[/latex].

[latex]M=\left(\frac{{x}_{1}+{x}_{2}}{2},\frac{{y}_{1}+{y}_{2}}{2}\right)[/latex]

A graphical view of a midpoint is shown below. Notice that the line segments on either side of the midpoint are congruent.

This is a line graph on an x, y coordinate plane with the x and y axes ranging from 0 to 6. The points (x sub 1, y sub 1), (x sub 2, y sub 2), and (x sub 1 plus x sub 2 all over 2, y sub 1 plus y sub 2 all over 2) are plotted. A straight line runs through these three points. Pairs of short parallel lines bisect the two sections of the line to note that they are equivalent.

Example: Finding the Midpoint of A Line Segment

Find the midpoint of the line segment with the endpoints [latex]\left(7,-2\right)[/latex] and [latex]\left(9,5\right)[/latex].

Try It

Find the midpoint of the line segment with endpoints [latex]\left(-2,-1\right)[/latex] and [latex]\left(-8,6\right)[/latex].

Try It

Complete the Square

We will use the example [latex]{x}^{2}+4x+1=0[/latex] to illustrate each step of completing the sqare. To complete the square, it is always easier when the leading coefficient, a, equals 1.

  1. Given a quadratic equation that cannot be factored and with [latex]a=1[/latex], first add or subtract the constant term to the right sign of the equal sign.
    [latex]{x}^{2}+4x=-1[/latex]
  2. Multiply the b term by [latex]\frac{1}{2}[/latex] and square it.
    [latex]\begin{array}{l}\frac{1}{2}\left(4\right)=2\hfill \\ {2}^{2}=4\hfill \end{array}[/latex]
  3. Add [latex]{\left(\frac{1}{2}b\right)}^{2}[/latex] to both sides of the equal sign and simplify the right side. We have
    [latex]\begin{array}{l}{x}^{2}+4x+4=-1+4\hfill \\ {x}^{2}+4x+4=3\hfill \end{array}[/latex]
  4. The left side of the equation can now be factored as a perfect square.
    [latex]\begin{array}{l}{x}^{2}+4x+4=3\hfill \\ {\left(x+2\right)}^{2}=3\hfill \end{array}[/latex]
  5. Use the square root property and solve.
    [latex]\begin{array}{l}\sqrt{{\left(x+2\right)}^{2}}=\pm \sqrt{3}\hfill \\ x+2=\pm \sqrt{3}\hfill \\ x=-2\pm \sqrt{3}\hfill \end{array}[/latex]
  6. The solutions are [latex]x=-2+\sqrt{3}[/latex], [latex]x=-2-\sqrt{3}[/latex].

We will see when studying conic sections that the method of completing the square comes in handy when rewriting the equation of a conic section given in general form. In preparation to use the method in this manner, it will be good to practice it first.

How To: use the method of complete the square to write a perfect square trinomial from an expression

  1. Given an expression of the form [latex]a\left(x^2+bx\right)[/latex], add [latex]\left(\dfrac{b}{2}\right)^2[/latex] inside the parentheses.
  2. Then subtract [latex]a\left(\dfrac{b}{2}\right)^2[/latex] to counteract the change you made to the expression.
  3. If completing the square on one side of an equation, you may either subtract the value of [latex]a\left(\dfrac{b}{2}\right)^2[/latex] from that side, or add it to the other to maintain equality.
  4.  Then factor the perfect square trinomial you created inside the original parentheses.

The resulting form will look like this:

Given

[latex]\qquad a\left(x^2+bx\right)[/latex]

add [latex]\left(b/2\right)^2[/latex] inside the parentheses and subtract [latex]a\left(b/2\right)^2[/latex] to counteract the change you made to the expression

[latex]=a\left(x^2+bx+ \left(\dfrac{b}{2}\right)^2\right)-a\left(\dfrac{b}{2}\right)^2[/latex]

then factor the resulting perfect square trinomial

[latex]=a\left(x+ \dfrac{b}{2}\right)^2-a\left(\dfrac{b}{2}\right)^2[/latex].

Example : CreatING a perfect square trinomial using the method of complete the square

Complete the square on: [latex]3\left(x^2 - 10x\right)[/latex].

try it