Learning Outcomes
- Solve systems of equations
- Describe how to use critical points to locate absolute extrema over a closed interval
In the Maxima/Minima Problems and Lagrange Multipliers sections, we will learn how to determine where a function of multiple variables is either maximized or minimized on a certain interval. Here we will review how to solve a system of equations in two variables and find the absolute extrema of a function of one variable.
Solve a System of Equations in Two Variables
A system of linear equations consists of two or more linear equations made up of two or more variables such that all equations in the system are considered simultaneously. To find the unique solution to a system of linear equations, we must find a numerical value for each variable in the system that will satisfy all equations in the system at the same time. Some linear systems may not have a solution and others may have an infinite number of solutions. In order for a linear system to have a unique solution, there must be at least as many equations as there are variables. Even so, this does not guarantee a unique solution.
We will first look at systems of linear equations in two variables, which consist of two equations that contain two different variables. For example, consider the following system of linear equations in two variables.
[latex]\begin{gathered}2x+y=15\\ 3x-y=5\end{gathered}[/latex]
The solution to a system of linear equations in two variables is any ordered pair that satisfies each equation independently. In this example, the ordered pair (4, 7) is the solution to the system of linear equations. We can verify the solution by substituting the values into each equation to see if the ordered pair satisfies both equations. Shortly we will investigate methods of finding such a solution if it exists.
[latex]\begin{align}2\left(4\right)+\left(7\right)&=15&&\text{True} \\ 3\left(4\right)-\left(7\right)&=5&&\text{True} \end{align}[/latex]
Two of the most common ways to solve a system of linear equations are the substitution method and the addition (elimination) method.
The Substitution Method
How To: Given a system of two equations in two variables, solve using the substitution method.
- Solve one of the two equations for one of the variables in terms of the other.
- Substitute the expression for this variable into the second equation, then solve for the remaining variable.
- Substitute that solution into either of the original equations to find the value of the first variable. If possible, write the solution as an ordered pair.
- Check the solution in both equations.
EXAMPLE: SOLVING A SYSTEM OF EQUATIONS USING THE SUBSTITUTION METHOD
Solve the following system of equations by substitution.
[latex]\begin{align}-x+y&=-5 \\ 2x-5y&=1 \end{align}[/latex]
Show Solution
First, we will solve the first equation for [latex]y[/latex].
[latex]\begin{align}-x+y&=-5 \\ y&=x - 5 \end{align}[/latex]
Now we can substitute the expression [latex]x - 5[/latex] for [latex]y[/latex] in the second equation.
[latex]\begin{align}2x - 5y&=1 \\ 2x - 5\left(x - 5\right)&=1 \\ 2x - 5x+25&=1 \\ -3x&=-24 \\ x&=8 \end{align}[/latex]
Now, we substitute [latex]x=8[/latex] into the first equation and solve for [latex]y[/latex].
[latex]\begin{align}-\left(8\right)+y&=-5 \\ y&=3 \end{align}[/latex]
Our solution is [latex]\left(8,3\right)[/latex].
Check the solution by substituting [latex]\left(8,3\right)[/latex] into both equations.
[latex]\begin{align}-x+y&=-5 \\ -\left(8\right)+\left(3\right)&=-5 && \text{True} \\[3mm] 2x - 5y&=1 \\ 2\left(8\right)-5\left(3\right)&=1 && \text{True} \end{align}[/latex]
The Addition (Elimination) Method
How To: Given a system of equations, solve using the addition method.
- Write both equations with x– and y-variables on the left side of the equal sign and constants on the right.
- Write one equation above the other, lining up corresponding variables. If one of the variables in the top equation has the opposite coefficient of the same variable in the bottom equation, add the equations together, eliminating one variable. If not, use multiplication by a nonzero number so that one of the variables in the top equation has the opposite coefficient of the same variable in the bottom equation, then add the equations to eliminate the variable.
- Solve the resulting equation for the remaining variable.
- Substitute that value into one of the original equations and solve for the second variable.
- Check the solution by substituting the values into the other equation.
Example: SOLVING A SYSTEM OF EQUATIONS USING THE ADDITION METHOD
Solve the given system of equations by addition.
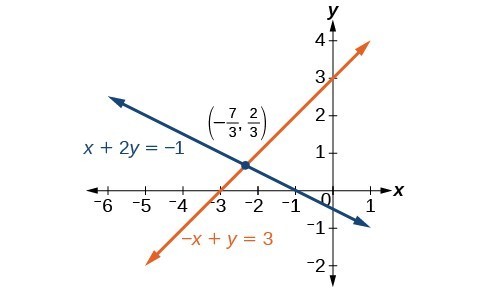
[latex]\begin{align}x+2y&=-1 \\ -x+y&=3 \end{align}[/latex]
Show Solution
Both equations are already set equal to a constant. Notice that the coefficient of [latex]x[/latex] in the second equation, –1, is the opposite of the coefficient of [latex]x[/latex] in the first equation, 1. We can add the two equations to eliminate [latex]x[/latex] without needing to multiply by a constant.
[latex]\begin{align} x+2y&=-1 \\ -x+y&=3 \\ \hline 3y&=2\end{align}[/latex]
Now that we have eliminated [latex]x[/latex], we can solve the resulting equation for [latex]y[/latex].
[latex]\begin{align}3y&=2 \\ y&=\dfrac{2}{3} \end{align}[/latex]
Then, we substitute this value for [latex]y[/latex] into one of the original equations and solve for [latex]x[/latex].
[latex]\begin{align}-x+y&=3 \\ -x+\frac{2}{3}&=3 \\ -x&=3-\frac{2}{3} \\ -x&=\frac{7}{3} \\ x&=-\frac{7}{3} \end{align}[/latex]
The solution to this system is [latex]\left(-\frac{7}{3},\frac{2}{3}\right)[/latex].
Check the solution in the first equation.
[latex]\begin{align}x+2y&=-1 \\ \left(-\frac{7}{3}\right)+2\left(\frac{2}{3}\right)&= \\ -\frac{7}{3}+\frac{4}{3}&= \\ -\frac{3}{3}&= \\ -1&=-1&& \text{True} \end{align}[/latex]
Analysis of the Solution
We gain an important perspective on systems of equations by looking at the graphical representation. See the graph below to find that the equations intersect at the solution. We do not need to ask whether there may be a second solution because observing the graph confirms that the system has exactly one solution.
Example: SOLVING A SYSTEM OF EQUATIONS USING THE ADDITION METHOD
Solve the given system of equations by the addition method.
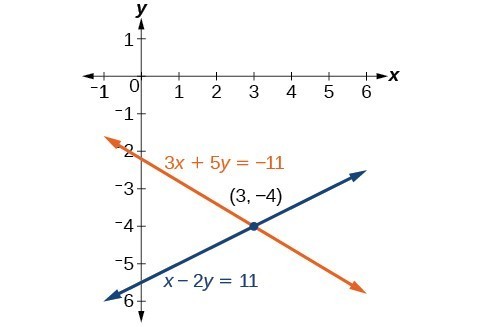
[latex]\begin{align}3x+5y&=-11 \\ x - 2y&=11 \end{align}[/latex]
Show Solution
Adding these equations as presented will not eliminate a variable. However, we see that the first equation has [latex]3x[/latex] in it and the second equation has [latex]x[/latex]. So if we multiply the second equation by [latex]-3,\text{}[/latex] the x-terms will add to zero.
[latex]\begin{align}x - 2y&=11 \\ -3\left(x - 2y\right)&=-3\left(11\right) && \text{Multiply both sides by }-3 \\ -3x+6y&=-33 && \text{Use the distributive property}. \end{align}[/latex]
Now, let’s add them.
[latex]\begin{align}3x+5y&=−11 \\ −3x+6y&=−33 \\ \hline 11y&=−44 \\ y&=−4 \end{align}[/latex]
For the last step, we substitute [latex]y=-4[/latex] into one of the original equations and solve for [latex]x[/latex].
[latex]\begin{align}3x+5y&=-11\\ 3x+5\left(-4\right)&=-11\\ 3x - 20&=-11\\ 3x&=9\\ x&=3\end{align}[/latex]
Our solution is the ordered pair [latex]\left(3,-4\right)[/latex]. Check the solution in the original second equation.
[latex]\begin{align}x - 2y&=11 \\ \left(3\right)-2\left(-4\right)&=3+8 \\ &=11 && \text{True} \end{align}[/latex]
Locating Absolute Extrema
The extreme value theorem states that a continuous function over a closed, bounded interval has an absolute maximum and an absolute minimum.
Location of Absolute Extrema
Let [latex]f[/latex] be a continuous function over a closed, bounded interval [latex]I[/latex]. The absolute maximum of [latex]f[/latex] over [latex]I[/latex] and the absolute minimum of [latex]f[/latex] over [latex]I[/latex] must occur at endpoints of [latex]I[/latex] or at critical points of [latex]f[/latex] in [latex]I[/latex].
How To: Given a Function, Locate the Absolute Extrema Over a Closed Interval [latex][a,b][/latex].
- Evaluate [latex]f[/latex] at the endpoints [latex]x=a[/latex] and [latex]x=b[/latex].
- Find all critical points of [latex]f[/latex] that lie over the interval [latex](a,b)[/latex] and evaluate [latex]f[/latex] at those critical points.
- Compare all values found in (1) and (2). From the location of absolute extrema, the absolute extrema must occur at endpoints or critical points. Therefore, the largest of these values is the absolute maximum of [latex]f[/latex]. The smallest of these values is the absolute minimum of [latex]f[/latex].
Example: Locating Absolute Extrema
For each of the following functions, find the absolute maximum and absolute minimum over the specified interval and state where those values occur.
- [latex]f(x)=−x^2+3x-2[/latex] over [latex][1,3][/latex].
- [latex]f(x)=x^2-3x^{\frac{2}{3}}[/latex] over [latex][0,2][/latex].
Show Solution
- Step 1. Evaluate [latex]f[/latex] at the endpoints [latex]x=1[/latex] and [latex]x=3[/latex].
[latex]f(1)=0[/latex] and [latex]f(3)=-2[/latex]
Step 2. Since [latex]f^{\prime}(x)=-2x+3[/latex], [latex]f^{\prime}[/latex] is defined for all real numbers [latex]x[/latex]. Therefore, there are no critical points where the derivative is undefined. It remains to check where [latex]f^{\prime}(x)=0[/latex]. Since [latex]f^{\prime}(x)=-2x+3=0[/latex] at [latex]x=\frac{3}{2}[/latex] and [latex]\frac{3}{2}[/latex] is in the interval [latex][1,3][/latex], [latex]f(\frac{3}{2})[/latex] is a candidate for an absolute extremum of [latex]f[/latex] over [latex][1,3][/latex]. We evaluate [latex]f(\frac{3}{2})[/latex] and find
[latex]f\left(\frac{3}{2}\right)=\frac{1}{4}[/latex]
Step 3. We set up the following table to compare the values found in steps 1 and 2.
| [latex]x[/latex] |
[latex]f(x)[/latex] |
Conclusion |
| 0 |
0 |
|
| [latex]\frac{3}{2}[/latex] |
[latex]\frac{1}{4}[/latex] |
Absolute maximum |
| 3 |
-2 |
Absolute minimum |
From the table, we find that the absolute maximum of [latex]f[/latex] over the interval [latex][1,3][/latex] is [latex]\frac{1}{4}[/latex], and it occurs at [latex]x=\frac{3}{2}[/latex]. The absolute minimum of [latex]f[/latex] over the interval [latex][1,3][/latex] is -2, and it occurs at [latex]x=3[/latex] as shown in the following graph.

This function has both an absolute maximum and an absolute minimum.
- Step 1. Evaluate [latex]f[/latex] at the endpoints [latex]x=0[/latex] and [latex]x=2[/latex].
[latex]f(0)=0[/latex] and [latex]f(2)=4-3\sqrt[3]{4}\approx -0.762[/latex]
Step 2. The derivative of [latex]f[/latex] is given by
[latex]f^{\prime}(x)=2x-\dfrac{2}{x^{\frac{1}{3}}}=\dfrac{2x^{\frac{4}{3}}-2}{x^{\frac{1}{3}}}[/latex]
for [latex]x\ne 0[/latex]. The derivative is zero when [latex]2x^{\frac{4}{3}}-2=0[/latex], which implies [latex]x=\pm 1[/latex]. The derivative is undefined at [latex]x=0[/latex]. Therefore, the critical points of [latex]f[/latex] are [latex]x=0,1,-1[/latex]. The point [latex]x=0[/latex] is an endpoint, so we already evaluated [latex]f(0)[/latex] in step 1. The point [latex]x=-1[/latex] is not in the interval of interest, so we need only evaluate [latex]f(1)[/latex]. We find that
[latex]f(1)=-2[/latex]
Step 3. We compare the values found in steps 1 and 2, in the following table.
| [latex]x[/latex] |
[latex]f(x)[/latex] |
Conclusion |
| 0 |
0 |
Absolute maximum |
| 1 |
-2 |
Absolute minimum |
| 2 |
-0.762 |
|
We conclude that the absolute maximum of [latex]f[/latex] over the interval [latex][0,2][/latex] is zero, and it occurs at [latex]x=0[/latex]. The absolute minimum is −2, and it occurs at [latex]x=1[/latex] as shown in the following graph.

This function has an absolute maximum at an endpoint of the interval.
Try It
Find the absolute maximum and absolute minimum of [latex]f(x)=x^2-4x+3[/latex] over the interval [latex][1,4][/latex].
Hint
Look for critical points. Evaluate [latex]f[/latex] at all critical points and at the endpoints.
Show Solution
The absolute maximum is 3 and it occurs at [latex]x=4[/latex]. The absolute minimum is -1 and it occurs at [latex]x=2[/latex].
Candela Citations
CC licensed content, Shared previously




