Learning Outcomes
- Plot points on a rectangular coordinate system
- Find the distance between two points
- Identify reference angles for angles measured in both radians and degrees
In the Vectors in the Plane section, we will look at quantities that have both magnitude and direction and how to work with them mathematically. Here we will review how to graph points on the coordinate plane, use the distance formula, and evaluate the sine and cosine functions at specific angle measures.
Plot Points
The Cartesian coordinate system, also called the rectangular coordinate system, is based on a two-dimensional plane consisting of the [latex]x[/latex]-axis and the [latex]y[/latex]-axis. Perpendicular to each other, the axes divide the plane into four sections. Each section is called a quadrant; the quadrants are numbered counterclockwise as shown in the figure below.
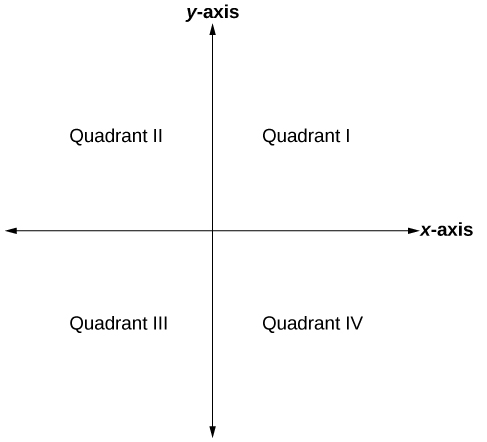
The Cartesian coordinate system with all four quadrants labeled.
The center of the plane is the point at which the two axes cross. It is known as the origin or point [latex]\left(0,0\right)[/latex].
Each point in the plane is identified by its [latex]{\bf{x}}-[/latex]coordinate, or horizontal displacement from the origin, and its [latex]{\bf{y}}-[/latex]coordinate, or vertical displacement from the origin. Together we write them as an ordered pair indicating the combined distance from the origin in the form [latex]\left(x,y\right)[/latex]. An ordered pair is also known as a coordinate pair because it consists of [latex]x[/latex] and [latex]y[/latex]-coordinates. For example, we can represent the point [latex]\left(3,-1\right)[/latex] in the plane by moving three units to the right of the origin in the horizontal direction and one unit down in the vertical direction.
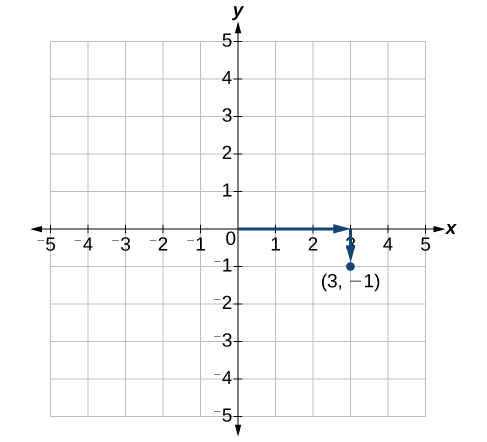
An illustration of how to plot the point (3,-1).
Cartesian Coordinate System
A two-dimensional plane where the
- [latex]x[/latex]-axis is the horizontal axis
- [latex]y[/latex]-axis is the vertical axis
A point in the plane is defined as an ordered pair, [latex]\left(x,y\right)[/latex], such that [latex]x[/latex] is determined by its horizontal distance from the origin and [latex]y[/latex] is determined by its vertical distance from the origin.
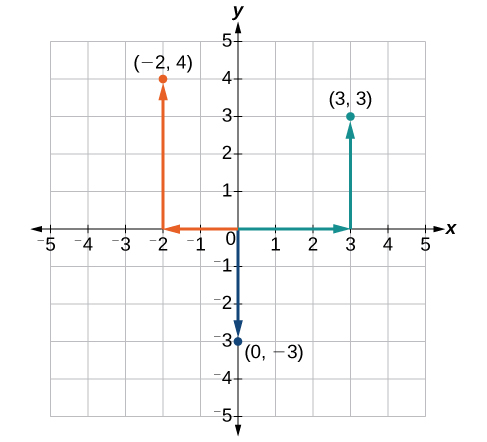
Example: Plotting Points in a Rectangular Coordinate System
Plot the points [latex]\left(-2,4\right)[/latex], [latex]\left(3,3\right)[/latex], and [latex]\left(0,-3\right)[/latex] in the coordinate plane.
Try It
Find the Distance Between Two Points
(also in Module 1, Skills Review for Conic Sections)
Derived from the Pythagorean Theorem, the distance formula is used to find the distance between two points in the plane. The Pythagorean Theorem, [latex]{a}^{2}+{b}^{2}={c}^{2}[/latex], is based on a right triangle where [latex]a[/latex] and [latex]b[/latex] are the lengths of the legs adjacent to the right angle, and [latex]c[/latex] is the length of the hypotenuse.
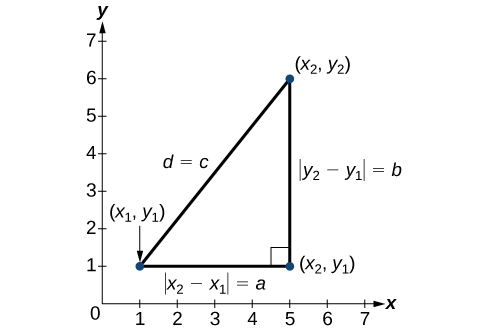
The relationship of sides [latex]|{x}_{2}-{x}_{1}|[/latex] and [latex]|{y}_{2}-{y}_{1}|[/latex] to side [latex]d[/latex] is the same as that of sides [latex]a[/latex] and [latex]b[/latex] to side [latex]c[/latex]. We use the absolute value symbol to indicate that the length is a positive number because the absolute value of any number is positive. (For example, [latex]|-3|=3[/latex]. ) The symbols [latex]|{x}_{2}-{x}_{1}|[/latex] and [latex]|{y}_{2}-{y}_{1}|[/latex] indicate that the lengths of the sides of the triangle are positive. To find the length [latex]c[/latex] , take the square root of both sides of the Pythagorean Theorem.
It follows that the distance formula is given as
We do not have to use the absolute value symbols in this definition because any number squared is positive.
A General Note: The Distance Formula
Given endpoints [latex]\left({x}_{1},{y}_{1}\right)[/latex] and [latex]\left({x}_{2},{y}_{2}\right)[/latex], the distance between two points is given by
Example: Finding the Distance between Two Points
Find the distance between the points [latex]\left(-3,-1\right)[/latex] and [latex]\left(2,3\right)[/latex].
Try It
Find the distance between two points: [latex]\left(1,4\right)[/latex] and [latex]\left(11,9\right)[/latex].
Find Reference Angles
(also in Module 1, Skills Review for Polar Coordinates)
You will learn that it is easiest to evaluate trigonometric functions when an angle is in the first quadrant. When the original angle is given in quadrant two, three, or four, a reference angle should be found.
An angle’s reference angle is the acute angle, [latex]t[/latex], formed by the terminal side of the angle [latex]t[/latex] and the horizontal axis. A reference angle is always an angle between [latex]0[/latex] and [latex]90^\circ[/latex], or [latex]0[/latex] and [latex]\frac{\pi }{2}[/latex] radians. As we can see in the figure below, for any angle in quadrants II, III, or IV, there is a reference angle in quadrant I.

A visual of the corresponding reference angles for each of the quadrants.
How To: Given an angle between [latex]0[/latex] and [latex]2\pi[/latex], find its reference angle.
- An angle in the first quadrant is its own reference angle.
- For an angle in the second or third quadrant, the reference angle is [latex]|\pi -t|[/latex] or [latex]|180^\circ \mathrm{-t}|[/latex].
- For an angle in the fourth quadrant, the reference angle is [latex]2\pi -t[/latex] or [latex]360^\circ \mathrm{-t}[/latex].
- If an angle is less than [latex]0[/latex] or greater than [latex]2\pi[/latex], add or subtract [latex]2\pi[/latex] as many times as needed to find an equivalent angle between [latex]0[/latex] and [latex]2\pi[/latex].
Example: Finding a Reference Angle
Find the reference angle of [latex]225^\circ[/latex] as shown in below.
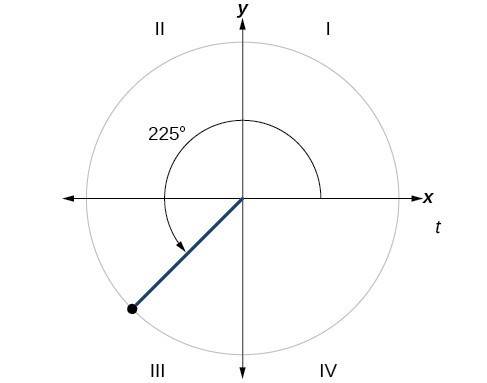
Try It
Find the reference angle of [latex]\frac{5\pi }{3}[/latex].
We can evaluate trigonometric functions of angles outside the first quadrant using reference angles. The quadrant of the original angle determines whether the answer is positive or negative. To help us remember which of the six trigonometric functions are positive in each quadrant, we can use the mnemonic phrase “A Smart Trig Class.” Each of the four words in the phrase corresponds to one of the four quadrants, starting with quadrant I and rotating counterclockwise. In quadrant I, which is “A,” all of the six trigonometric functions are positive. In quadrant II, “Smart,” only sine and its reciprocal function, cosecant, are positive. In quadrant III, “Trig,” only tangent and its reciprocal function, cotangent, are positive. Finally, in quadrant IV, “Class,” only cosine and its reciprocal function, secant, are positive.
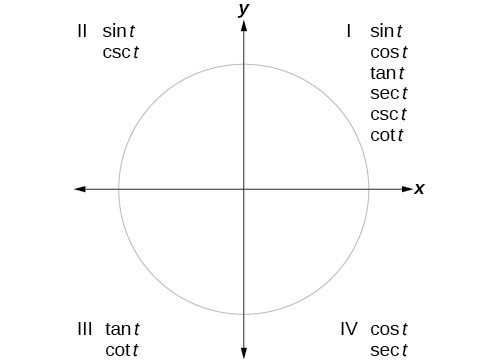
An illustration of which trigonometric functions are positive in each of the quadrants.
The unit circle tells us the value of cosine and sine at any of the given angle measures seen below. The first coordinate in each ordered pair is the value of cosine at the given angle measure, while the second coordinate in each ordered pair is the value of sine at the given angle measure. All trigonometric functions can be written in terms of sine and cosine. Thus, if you can evaluate sine and cosine at various angle values, you can also evaluate the other trigonometric functions at various angle values. Take time to learn the [latex]\left(x,y\right)[/latex] coordinates of all of the major angles in the first quadrant of the unit circle.
Remember, every angle in quadrant two, three, or four has a reference angle that lies in quadrant one. The quadrant of the original angle only affects the sign (positive or negative) of a trigonometric function’s value at a given angle.
How To: Given the angle of a point on The Unit circle, find the Value of Cosine (Or Sine) using quadrant one.
- Find the reference angle using the appropriate reference angle formula from the first portion of this review section.
- Find the value of cosine (or sine) at the reference angle by looking at quadrant one of the unit circle.
- Determine the appropriate sign of your found value for cosine (or sine) based on the quadrant of the original angle.
Example: Using the Unit Circle to Find the Value of cosine
Use quadrant one of the unit circle to find the value of cosine at an angle of [latex]\frac{7\pi }{6}[/latex].
Try It
Use quadrant one of the unit circle to find the value of sine at an angle of [latex]\frac{5\pi }{3}[/latex].
Candela Citations
- Calculus Volume 1. Provided by: Lumen Learning. Located at: https://courses.lumenlearning.com/calculus1/. License: CC BY: Attribution
- Calculus Volume 2. Provided by: Lumen Learning. Located at: https://courses.lumenlearning.com/calculus2/. License: CC BY: Attribution