The Cross Product

Learning Objectives

  • Calculate the cross product of two given vectors.
  • Use determinants to calculate a cross product.

The Cross Product and Its Properties

The dot product is a multiplication of two vectors that results in a scalar. In this section, we introduce a product of two vectors that generates a third vector orthogonal to the first two. Consider how we might find such a vector. Let [latex]\mathbf{u} =\langle u_1, u_2, u_3 \rangle[/latex] and [latex]\mathbf{v} =\langle v_1, v_2, v_3 \rangle[/latex] be nonzero vectors. We want to find a vector [latex]\mathbf{w} =\langle w_1, w_2, w_3 \rangle[/latex] orthogonal to both [latex]\mathbf{u}[/latex] and [latex]\mathbf{v}[/latex]—that is, we want to find [latex]\mathbf{w}[/latex] such that [latex]\mathbf{u} \cdot \mathbf{w} = 0[/latex] and [latex]\mathbf{v} \cdot \mathbf{w} =0[/latex]. Therefore, [latex]w_1[/latex], [latex]w_2[/latex], and [latex]w_3[/latex] must satisfy

[latex]\begin{aligned} u_1w_1 + u_2w_2 + u_3w_3 &= 0 \\ v_1w_1 + v_2w_2 + v_3w_3 &= 0.\\ \end{aligned}[/latex]

If we multiply the top equation by [latex]v_3[/latex] and the bottom equation by [latex]u_3[/latex] and subtract, we can eliminate the variable [latex]w_3[/latex], which gives

[latex](u_1v_3 - v_1u_3)w_1 + (u_2v_3 - v_2u_3)w_2 = 0[/latex].

If we select

[latex]\begin{align*} w_1 &= u_2v_3 - v_2u_3\\ w_2 &= -(u_1v_3 - u_3v_1),\\ \end{align*}[/latex]

we get a possible solution vector. Substituting these values back into the original equations gives

[latex]w_3 = u_1v_2 - u_2v_1[/latex].

That is, vector

[latex]\mathbf{w} = \langle u_2v_3 - u_3v_2, -(u_1v_3 - u_3v_1), u_1v_2 - u_2v_1 \rangle[/latex]

is orthogonal to both [latex]\textbf u[/latex] and [latex]\textbf v[/latex], which leads us to define the following operation, called the cross product.

DEFINITION

Let [latex]\mathbf{u} =\langle u_1, u_2, u_3 \rangle[/latex] and [latex]\mathbf{v} =\langle v_1, v_2, v_3 \rangle[/latex]. Then, the cross product [latex]\mathbf{u} \times \mathbf{v}[/latex] is vector

[latex]\begin{align*} \mathbf{u} \times \mathbf{v} &= (u_2v_3 - u_3v_2)\mathbf{i} -(u_1v_3 - u_3v_1)\mathbf{j}+ (u_1v_2 - u_2v_1)\mathbf{k}\\ &= \langle u_2v_3 - u_3v_2, -(u_1v_3 - u_3v_1), u_1v_2 - u_2v_1 \rangle.\\ \end{align*}[/latex]

From the way we have developed [latex]\mathbf{u} \times \mathbf{v}[/latex], it should be clear that the cross product is orthogonal to both [latex]\textbf u[/latex] and [latex]\textbf v[/latex]. However, it never hurts to check. To show that [latex]\mathbf{u} \times \mathbf{v}[/latex] is orthogonal to [latex]\textbf u[/latex], we calculate the dot product of [latex]\textbf u[/latex] and [latex]\mathbf{u} \times \mathbf{v}[/latex].

[latex]\begin{align*} \mathbf{u} \cdot (\mathbf{u} \times \mathbf{v}) &= \langle u_1,u_2,u_3 \rangle \cdot \langle u_2v_3 - u_3v_2, -u_1v_3 - u_3v_1, u_1v_2 - u_2v_1 \rangle\\ &= u_1(u_2v_3 - u_3v_2) + u_2 (-u_1v_3 + u_3v_1) +u_3( u_1v_2 - u_2v_1)\\ &= u_1u_2v_3 - u_1u_3v_2 -u_1u_2v_3+u_2u_3v_1 +u_1u_3v_2-u_2u_3v_1\\ &= (u_1u_2v_3 - u_1u_2v_3) +(-u_1u_3v_2+u_1u_3v_2) + (u_2u_3v_1-u_2u_3v_1)\\ &= 0\\ \end{align*}[/latex]

In a similar manner, we can show that the cross product is also orthogonal to [latex]\textbf v[/latex].

Example: finding a cross product

Let [latex]\mathbf{p} =\langle -1,2,5 \rangle[/latex] and [latex]\mathbf{q} =\langle 4,0,-3 \rangle[/latex] (Figure 1). Find [latex]\mathbf{p} \times \mathbf{q}[/latex].

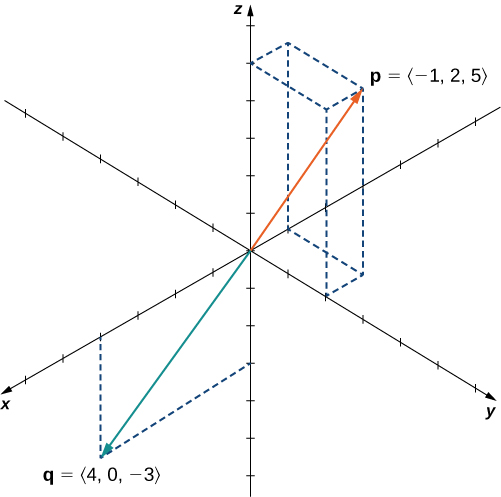
This figure is the 3-dimensional coordinate system. It has two vectors in standard position. The first vector is labeled “p = <-1, 2, 5>.” The second vector is labeled “q = <4, 0, -3>.”

Figure 1. Finding a cross product to two given vectors.

try it

Find [latex]\mathbf{p} \times \mathbf{q}[/latex] for [latex]\mathbf{p} =\langle 5,1,2 \rangle[/latex] and [latex]\mathbf{q} =\langle -2,0,1 \rangle[/latex]. Express the answer using standard unit vectors.

Watch the following video to see the worked solution to the above Try IT.

You can view the transcript for “CP 2.30” here (opens in new window).

Try It

Although it may not be obvious from the Cross Product Equation, the direction of [latex]\mathbf{u} \times \mathbf{v}[/latex] is given by the right-hand rule. If we hold the right hand out with the fingers pointing in the direction of [latex]\textbf u[/latex], then curl the fingers toward vector [latex]\textbf v[/latex], the thumb points in the direction of the cross product, as shown.

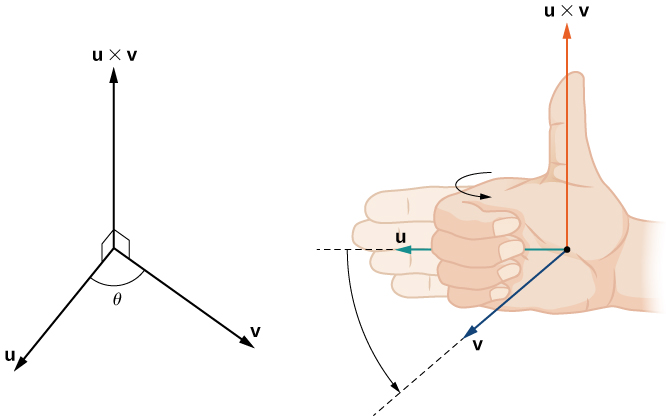
This figure has two images. The first image has three vectors with the same initial point. Two of the vectors are labeled “u” and “v.” The angle between u and v is theta. The third vector is perpendicular to u and v. It is labeled “u cross v.” The second image has three vectors. The vectors are labeled “u, v, and u cross v.” “u cross v” is perpendicular to u and v. Also, on the image of these three vectors is a right hand. The fingers are in the direction of u. As the hand is closing, the direction of the closing fingers is the direction of v. The thumb is up and in the direction of “u cross v.”

Figure 2. The direction of [latex]{\bf{u}}\times{\bf{v}}[/latex] is determined by the right-hand rule.

Notice what this means for the direction of [latex]\mathbf{v} \times \mathbf{u}[/latex]. If we apply the right-hand rule to [latex]\mathbf{v} \times \mathbf{u}[/latex], we start with our fingers pointed in the direction of [latex]\textbf v[/latex], then curl our fingers toward the vector [latex]\textbf u[/latex]. In this case, the thumb points in the opposite direction of [latex]\mathbf{u} \times \mathbf{v}[/latex]. (Try it!)

Example: anticommutativity of the cross product

Let [latex]\mathbf{u} =\langle 0,2,1 \rangle[/latex] and [latex]\mathbf{v} =\langle 3,-1,0 \rangle[/latex]. Calculate [latex]\mathbf{u} \times \mathbf{v}[/latex] and [latex]\mathbf{v} \times \mathbf{u}[/latex] and graph them.

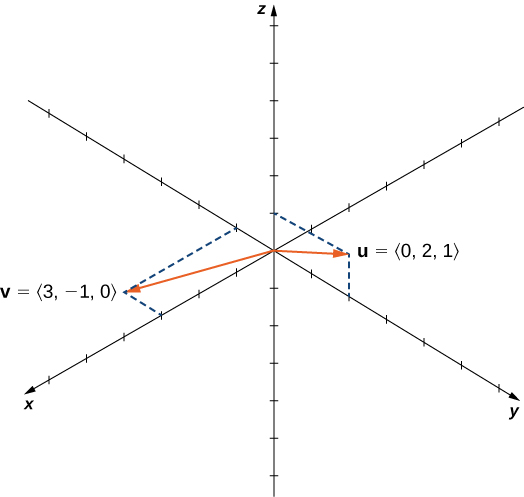
This figure is the 3-dimensional coordinate system. It has two vectors in standard position. The first vector is labeled “u = <0, 2, 1>.” The second vector is labeled “v = <3, -1, 0>.”

Figure 3. Are the cross products [latex]{\bf{u}}\times{\bf{v}}[/latex] and [latex]{\bf{v}}\times{\bf{u}}[/latex] in the same direction?

try it

Suppose vectors [latex]\textbf u[/latex] and [latex]\textbf v[/latex] lie in the [latex]xy[/latex]-plane (the [latex]z[/latex]-component of each vector is zero). Now suppose the [latex]x[/latex]– and [latex]y[/latex]-components of [latex]\textbf u[/latex] and the [latex]y[/latex]-component of [latex]\textbf v[/latex] are all positive, whereas the [latex]x[/latex]-component of [latex]\textbf v[/latex] is negative. Assuming the coordinate axes are oriented in the usual positions, in which direction does [latex]\mathbf{u} \times \mathbf{v}[/latex] point?

The cross products of the standard unit vectors [latex]\textbf i[/latex], [latex]\textbf j[/latex], and [latex]\textbf k[/latex] can be useful for simplifying some calculations, so let’s consider these cross products. A straightforward application of the definition shows that

[latex]\mathbf{i} \times \mathbf{i} = \mathbf{j} \times \mathbf{j}= \mathbf{k} \times \mathbf{k} = 0[/latex].

(The cross product of two vectors is a vector, so each of these products results in the zero vector, not the scalar 0.) It’s up to you to verify the calculations on your own.

Furthermore, because the cross product of two vectors is orthogonal to each of these vectors, we know that the cross product of [latex]\textbf i[/latex] and [latex]\textbf j[/latex] is parallel to [latex]\textbf k[/latex]. Similarly, the vector product of [latex]\textbf i[/latex] and [latex]\textbf k[/latex] is parallel to [latex]\textbf j[/latex], and the vector product of [latex]\textbf j[/latex] and [latex]\textbf k[/latex] is parallel to [latex]\textbf i[/latex]. We can use the right-hand rule to determine the direction of each product. Then we have

[latex]\begin{aligned} \mathbf{i} \times \mathbf{j} &= \mathbf{k} & \mathbf{j} \times \mathbf{i} &= -\mathbf{k}\\ \mathbf{j} \times \mathbf{k} &= \mathbf{i} & \mathbf{k} \times \mathbf{j} &= -\mathbf{i} \\ \mathbf{k} \times \mathbf{i} &= \mathbf{j} & \mathbf{i} \times \mathbf{k} &= -\mathbf{j}.\\\end{aligned}[/latex]

These formulas come in handy later.

Example: cross product of standard unit vectors

Find [latex]\mathbf{i} \times (\mathbf{j} \times \mathbf{k})[/latex].

try it

Find [latex](\mathbf{i} \times \mathbf{j}) \times (\mathbf{k} \times \mathbf{i})[/latex].

As we have seen, the dot product is often called the scalar product because it results in a scalar. The cross product results in a vector, so it is sometimes called the vector product. These operations are both versions of vector multiplication, but they have very different properties and applications. Let’s explore some properties of the cross product. We prove only a few of them. Proofs of the other properties are left as exercises.

THEOREM: properties of the cross product

Let [latex]\textbf u[/latex], [latex]\textbf v[/latex], and [latex]\textbf w[/latex] be vectors in space, and let [latex]c[/latex] be a scalar.

\[ \begin{array}{lrl}
\mbox{i.} & \mathbf{u \times v} &= -( \mathbf{v \times u}) & \mbox{Anticommutative property} \\
\mbox{ii.} & \mathbf{u} \times (\mathbf{v} + \textbf{w}) &= \mathbf{u \times v} + \mathbf{u \times w} & \mbox{Distributive property} \\
\mbox{iii.} & c(\mathbf{u \times v}) &= (c\mathbf{u}) \times \mathbf{v} = \mathbf{u} \times (c\mathbf{v}) & \mbox{ Multiplication by a constant} \\
\mbox{iv.} & \mathbf{u} \times \mathbf{0} &= \mathbf{0} \times \mathbf{u} = \mathbf{0} & \mbox{ Cross product of the zero vector} \\
\mbox{iv.} & \mathbf{v} \times \mathbf{v} &= \mathbf{0} & \mbox{  Cross product of a vector with itself} \\
\mbox{iv.} & \mathbf{u} \times (\mathbf{v} \times \textbf{w}) &= (\mathbf{u} \times \textbf{v}) \times \mathbf{w} & \mbox{ Scalar triple product} \\
\end{array}\]

Proof

For property i., we want to show [latex]\mathbf{u \times v} = -( \mathbf{v \times u})[/latex]. We have

[latex]\begin{align*} \mathbf{u} \times \mathbf{v} &= \langle u_1, u_2, u_3 \rangle \times \langle v_1, v_2, v_3 \rangle\\ &= \langle u_2v_3 - u_3v_2, -u_1v_3 + u_3v_1, u_1v_2 - u_2v_1 \rangle \\ &= -\langle u_3v_2 - u_2v_3, -u_3v_1 + u_1v_3, u_2v_1 - u_1v_2 \rangle\\ &= -\langle v_1, v_2, v_3 \rangle \times \langle u_1, u_2, u_3 \rangle \\ &= -( \mathbf{v \times u}).\\ \end{align*}[/latex]

 

Unlike most operations we’ve seen, the cross product is not commutative. This makes sense if we think about the right-hand rule.

For property iv., this follows directly from the definition of the cross product. We have

[latex]\begin{align*} \mathbf{u} \times \mathbf{0} &= \langle u_2(0) - u_3(0), -(u_2(0) - u_3(0)), u_1(0) - u_2(0) \rangle\\ &= \langle 0,0,0\rangle = \mathbf{0}.\\ \end{align*}[/latex]

Then, by property i., [latex]\mathbf{0} \times \mathbf{u} = \mathbf{0}[/latex] as well. Remember that the dot product of a vector and the zero vector is the scalar [latex]0[/latex], whereas the cross product of a vector with the zero vector is the vector [latex]\textbf 0[/latex].

Property vi. looks like the associative property, but note the change in operations:

[latex]\begin{align*} \mathbf{u} \cdot (\mathbf{v \times w}) &= \mathbf{u} \cdot \langle v_2w_3 - v_3w_2, -v_1w_3 + v_3w_1,v_1w_2 - v_2w_1 \rangle\\ &= u_1(v_2w_3 - v_3w_2) + u_2(-v_1w_3 + v_3w_1) + u_3(v_1w_2 - v_2w_1) \\ &= u_1v_2w_3 - u_1v_3w_2 - u_2v_1w_3 + u_2v_3w_1 + u_3v_1w_2 - u_3v_2w_1 \\ &= (u_2v_3 - u_3v_2)w_1 + (u_3v_1 - u_1v_3)w_2 + (u_1v_2 - u_2v_1)w_3\\ &= \langle u_2v_3 - u_3v_2,u_3v_1 - u_1v_3, u_1v_2 - u_2v_1 \rangle \times \langle w_1, w_2, w_3 \rangle \\ &= (\mathbf{u \times v}) \cdot \mathbf{w}.\\ \end{align*}[/latex]

 

[latex]_\blacksquare[/latex]

Example: using the properties of the cross product

Use the cross product properties to calculate [latex](2\mathbf{i} \times 3\mathbf{j}) \times \mathbf{j}[/latex].

try it

Use the cross product properties to calculate [latex](\mathbf{i} \times \mathbf{k}) \times (\mathbf{k} \times \mathbf{j})[/latex].

So far in this section, we have been concerned with the direction of the vector [latex]\mathbf{u} \times \mathbf{v}[/latex], but we have not discussed its magnitude. It turns out there is a simple expression for the magnitude of [latex]\mathbf{u} \times \mathbf{v}[/latex] involving the magnitudes of [latex]\mathbf u[/latex] and [latex]\mathbf v[/latex], and the sine of the angle between them.

THEOREM: magnitude of the cross product

Let [latex]\mathbf u[/latex] and [latex]\mathbf v[/latex] be vectors, and let [latex]\theta[/latex] be the angle between them. Then, [latex]||\mathbf{u} \times \mathbf{v}|| = ||\mathbf{u}|| \cdot ||\mathbf{v}||\cdot \sin{\theta}[/latex].

Proof

Let [latex]\mathbf{u} = \langle u_1,u_2, u_3\rangle[/latex] and [latex]\mathbf{v} = \langle v_1,v_2, v_3\rangle[/latex] be vectors, and let [latex]\theta[/latex] denote the angle between them. Then

[latex]\begin{align*} ||\mathbf{u} \times \mathbf{v}||^2 &= (u_2v_3 - u_3v_2)^2 + (u_3v_1 - u_1v_3)^2 + (u_1v_2 - u_2v_1)^2 \\ &= u_2^2v_3^2 -2u_2u_3v_2v_3 + u_3^2v_2^2 + u_3^2v_1^2 -2u_1u_3v_1v_3 + u_1^2v_3^2 + u_1^2v_2^2 -2u_1u_2v_1v_2 + u_2^2v_1^2 \\ &= u_1^2v_1^2 + u_1^2v_2^2 + u_1^2v_3^2 +u_2^2v_1^2 + u_2^2v_2^2 +u_2^2v_3^2 +u_3^2v_1^2 +u_3^2v_2^2+u_3^2v_3^2 - (u_1^2v_1^2 + u_2^2v_2^2 +u_3^2v_3^2 +2u_1u_2v_1v_2 + 2u_1u_3v_1v_3 + 2u_2u_3v_2v_3) \\ &= (u_1^2 + u_2^2 + u_3^2)(v_1^2 +v_2^2+v_3^2) - (u_1v_1 + u_2v_2 +u_3v_3)^2 \\ &= ||\mathbf{u}||^2||\mathbf{v}||^2 - (\mathbf{u} \cdot \mathbf{v})^2 \\ &= ||\mathbf{u}||^2||\mathbf{v}||^2 - ||\mathbf{u}||^2||\mathbf{v}||^2\cos^2{\theta} \\ &= ||\mathbf{u}||^2||\mathbf{v}||^2 - (1-\cos^2{\theta}) \\ &= ||\mathbf{u}||^2||\mathbf{v}||^2 - (\sin^2{\theta}). \\ \end{align*}[/latex]

 

Taking square roots and noting that [latex]\sqrt{\sin^2{\theta}} = \sin{\theta}[/latex] for [latex]0\geq \theta \geq 180[/latex], we have the desired result:

[latex]||\mathbf{u} \times \mathbf{v}|| = ||\mathbf{u}||\;||\mathbf{v}||\;\sin{\theta}[/latex].
[latex]_\blacksquare[/latex]

This definition of the cross product allows us to visualize or interpret the product geometrically. It is clear, for example, that the cross product is defined only for vectors in three dimensions, not for vectors in two dimensions. In two dimensions, it is impossible to generate a vector simultaneously orthogonal to two nonparallel vectors.

Example: calculating the cross product

Use Properties of the Cross Product to find the magnitude of the cross product of [latex]\mathbf{u} = \langle 0,4,0\rangle[/latex] and [latex]\mathbf{v} = \langle 0,0,-3\rangle[/latex].

try it

Use Properties of the Cross Product to find the magnitude of [latex]\mathbf{u} \times \mathbf{v}[/latex], where [latex]\mathbf{u} = \langle -8,0,0\rangle[/latex] and [latex]\mathbf{v} = \langle 0,2,0\rangle[/latex].

Determinants and the Cross Product

Using the Cross Product Equation to find the cross product of two vectors is straightforward, and it presents the cross product in the useful component form. The formula, however, is complicated and difficult to remember. Fortunately, we have an alternative. We can calculate the cross product of two vectors using determinant notation.

A [latex]2 \times 2[/latex] determinant is defined by

[latex]\begin{vmatrix} a_1 & a_2 \\ b_1 & b_2 \end{vmatrix} = a_1b_2 - b_1a_2[/latex].

For example,

[latex]\begin{vmatrix} 3 & -2 \\ 5 & 1 \end{vmatrix} = 3(1) - 5(-2) = 3+10 = 13[/latex].

A [latex]3 \times 3[/latex] determinant is defined in terms of [latex]2 \times 2[/latex] determinants as follows:

[latex]\begin{vmatrix} a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3\end{vmatrix} = a_1\begin{vmatrix} b_2 & b_3 \\ c_2 & c_3 \end{vmatrix} - a_2 \begin{vmatrix} b_1 & b_3 \\ c_1 & c_3 \end{vmatrix} + a_3\begin{vmatrix} b_1 & b_2 \\ c_1 & c_2 \end{vmatrix}[/latex].

Equation 2.10 is referred to as the expansion of the determinant along the first row. Notice that the multipliers of each of the [latex]2 \times 2[/latex] determinants on the right side of this expression are the entries in the first row of the [latex]3 \times 3[/latex] determinant. Furthermore, each of the [latex]2 \times 2[/latex] determinants contains the entries from the [latex]3 \times 3[/latex] determinant that would remain if you crossed out the row and column containing the multiplier. Thus, for the first term on the right, [latex]a_1[/latex] is the multiplier, and the [latex]2 \times 2[/latex] determinant contains the entries that remain if you cross out the first row and first column of the [latex]3 \times 3[/latex] determinant. Similarly, for the second term, the multiplier is [latex]a_2[/latex], and the [latex]2 \times 2[/latex] determinant contains the entries that remain if you cross out the first row and second column of the [latex]3 \times 3[/latex] determinant. Notice, however, that the coefficient of the second term is negative. The third term can be calculated in similar fashion.

Example: using Expansion along the first row to compute a [latex]3 \times 3[/latex] determinant

Evaluate the determinant [latex]\begin{vmatrix} 2 & 5 & -1 \\ -1 & 1 & 3 \\ -2 & 3 & 4\end{vmatrix}[/latex].

try it

Evaluate the determinant [latex]\begin{vmatrix} 1 & -2 & -1 \\ 3 & 2 & -3 \\ 1 & 5 & 4\end{vmatrix}[/latex].

Technically, determinants are defined only in terms of arrays of real numbers. However, the determinant notation provides a useful mnemonic device for the cross product formula.

RULE: CROSS PRODUCT CALCULATED BY A DETERMINANT

Let [latex]\mathbf{u} = \langle u_1,u_2, u_3\rangle[/latex] and [latex]\mathbf{v} = \langle v_1,v_2, v_3\rangle[/latex] be vectors. Then the cross product [latex]\mathbf{u} \times \mathbf{v}[/latex] is given by

[latex]\mathbf{u} \times \mathbf{v} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ u_1 & u_2 & u_3 \\ v_1 & v_2 & v_3\end{vmatrix} = \begin{vmatrix} u_2 & u_3 \\ v_2 & v_3 \end{vmatrix}\mathbf{i}-\begin{vmatrix} u_1 & u_3 \\ v_1 & v_3 \end{vmatrix}\mathbf{j} + \begin{vmatrix} u_1 & u_2 \\ v_1 & v_2 \end{vmatrix}\mathbf{k}[/latex].

Example: using determinant notation to find [latex]\mathbf{p} \times \mathbf{q}[/latex]

Let [latex]\mathbf{p} = \langle -1,2,5\rangle[/latex] and [latex]\mathbf{q} = \langle 4,0,-3\rangle[/latex]. Find [latex]\mathbf{p} \times \mathbf{q}[/latex].

try it

Use determinant notation to find [latex]\mathbf{a} \times \mathbf{b}[/latex], where [latex]\mathbf{a} = \langle 8,2,3\rangle[/latex] and [latex]\mathbf{b} = \langle -1,0,4\rangle[/latex].

Watch the following video to see the worked solution to the above Try IT.

You can view the transcript for “CP 2.36” here (opens in new window).