A reversible heat pump is a climate-control system that is an air conditioner and a heater in a single device. Operated in one direction, it pumps heat out of a house to provide cooling. Operating in reverse, it pumps heat into the building from the outside, even in cool weather, to provide heating. As a heater, a heat pump is several times more efficient than conventional electrical resistance heating.
If some physical machines can run in two directions, we might ask whether some of the function “machines” we have been studying can also run backwards. Figure below provides a visual representation of this question. In this section, we will consider the reverse nature of functions.

Verifying That Two Functions Are Inverse Functions
Suppose a fashion designer traveling to Milan for a fashion show wants to know what the temperature will be. He is not familiar with the Celsius scale. To get an idea of how temperature measurements are related, he asks his assistant, Betty, to convert 75 degrees Fahrenheit to degrees Celsius. She finds the formula
and substitutes 75 for F to calculate
Knowing that a comfortable 75 degrees Fahrenheit is about 24 degrees Celsius, he sends his assistant the week’s weather forecast for Milan, and asks her to convert all of the temperatures to degrees Fahrenheit.

At first, Betty considers using the formula she has already found to complete the conversions. After all, she knows her algebra, and can easily solve the equation for F after substituting a value for C. For example, to convert 26 degrees Celsius, she could write
After considering this option for a moment, however, she realizes that solving the equation for each of the temperatures will be awfully tedious. She realizes that since evaluation is easier than solving, it would be much more convenient to have a different formula, one that takes the Celsius temperature and outputs the Fahrenheit temperature.
The formula for which Betty is searching corresponds to the idea of an inverse function, which is a function for which the input of the original function becomes the output of the inverse function and the output of the original function becomes the input of the inverse function.
Informally, this means that inverse functions “undo” each other. However, just as zero does not have a reciprocal, some functions do not have inverses.
Given a function [latex]f(x)[/latex] we represent its inverse as [latex] f^{-1} (x) [/latex], read as “f inverse of x”. The raised -1 is part of the notation. It is not an exponent; it does not imply a power of -1. In other words, [latex] f^{-1} (x) [/latex] does not mean [latex]\frac{1}{f(x)} [/latex] because [latex]\frac{1}{f(x)} [/latex] is the reciprocal of [latex]f(x)[/latex] and not the inverse.
Inverse Function
For any one-to-one function [latex]f(x)=y[/latex] a function [latex] f^{-1} (x) [/latex] is an inverse function of [latex] f [/latex] if [latex] f^{-1} (y)=x [/latex]. This can also be written as [latex] f^{-1} (f(x))=x [/latex] for all [latex]x[/latex] in the domain of [latex]f[/latex]. It also follows that [latex]f(f^{-1} (x))=x [/latex] for all [latex]x[/latex] in the domain of [latex]f^{-1}[/latex] if [latex] f^{-1} (x) [/latex] is the inverse of [latex] f [/latex].
Identifying an Inverse Function for a Given Input-Output Pair
If for a particular one-to-one function [latex]f(2)=4[/latex] and [latex]f(5)=12[/latex] what are the corresponding input and output values for the inverse function?
The inverse function reverses the input and output quantities, so if
Alternatively, if we want to name the inverse function [latex]g[/latex] then [latex]g(4)=2[/latex] and [latex]g(12)=5[/latex] .
Analysis
Notice that if we show the coordinate pairs in a table form, the input and output are clearly reversed.
| [latex](x,f(x))[/latex] | [latex](x,g(x))[/latex] |
|---|---|
| (2,4) | (4,2) |
| (5,12) | (12,5) |
Is it possible for a function to have more than one inverse?
No. If two supposedly different functions, say g and h, both meet the definition of being inverses of another function f, then you can prove that g=h. On any one domain, the original function has only one unique inverse.
Finding and Evaluating Inverse Functions
Once we have a one-to-one function, we can evaluate its inverse at specific inverse function inputs or construct a complete representation of the inverse function in many cases.
Inverting Tabular Functions
Suppose we want to find the inverse of a function represented in table form. Remember that the domain of a function is the range of the inverse and the range of the function is the domain of the inverse. So we need to interchange the domain and range.
Each row (or column) of inputs becomes the row (or column) of outputs for the inverse function. Similarly, each row (or column) of outputs becomes the row (or column) of inputs for the inverse function.
Example: Interpreting the Inverse of a Tabular Function
A function [latex]f(t)[/latex] is given in Figure below, showing distance in miles that a car has traveled in t minutes. Find and interpret [latex]f^{-1}[/latex] .
| t, minutes | 30 | 50 | 70 | 90 |
| f(t), miles | 20 | 40 | 60 | 70 |
Try it
Using previous Figure, find and interpret (a) [latex]f(60)[/latex], and (b) [latex]f^{-1}(60)[/latex].
Given the graph of a function, evaluate its inverse at specific points.
- Find the desired input on the y-axis of the given graph.
- Read the inverse function’s output from the x-axis of the given graph.
ExAMPLE: Evaluating a Function and Its Inverse from a Graph at Specific Points
A function [latex]g(x)[/latex] is given below. Find [latex]g(3)[/latex], and [latex]g^{-1}(3)[/latex].
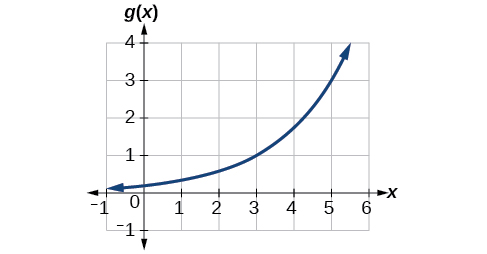
To evaluate [latex]g(3)[/latex] we find 3 on the x-axis and find the corresponding output value on the y-axis. The point (3,1) tells us that [latex]g(3)=1[/latex].
To evaluate [latex]g^{-1}(3)[/latex] recall that by definition [latex]g^{-1}(3)[/latex] means the value of x for which [latex]g(x)=3[/latex]. By looking for the output value 3 on the vertical axis, we find the point (5,3) on the graph, which means [latex]g(5)=3[/latex] so by definition, [latex]g^{-1}(3)=5[/latex]. See Figure below.

Sometimes we will need to know an inverse function for all elements of its domain, not just a few. If the original function is given as a formula, for example y as a function of x, we can often find the inverse function by solving the formula to obtain x as a function of y.
Given a function represented by a formula, find the inverse.
- Make sure [latex]f(x)=y[/latex] is a one-to-one function.
- Solve for x.
- Interchange x and y.
Example: Inverting the Fahrenheit-to-Celsius Function
Given [latex]C=\frac{5}{9}\left(F-32\right)[/latex], find a formula for the inverse function that gives Fahrenheit temperature as a function of Celsius temperature.
By solving in general, we have uncovered the inverse function. If [latex]Ch(F)=\frac{5}{9}\left(F-32\right)[/latex]
then
In this case, we introduced a function h to represent the conversion because the input and output variables are descriptive, and writing [latex]{C}^{-1}[/latex] could get confusing.
try it
Solve for x in terms of y, given [latex]y=\frac{1}{3}\left(x-5\right)[/latex].
Watch the following video for a review of the concept of inverse functions.
Key Concepts
- For a function to have an inverse, it must be one-to-one (pass the horizontal line test).
- For a tabular function, exchange the input and output rows to obtain the inverse.
- The inverse of a function can be determined at specific points on its graph.