Using the Law of Sines to Solve Oblique Triangles

In any triangle, we can draw an altitude, a perpendicular line from one vertex to the opposite side, forming two right triangles. It would be preferable, however, to have methods that we can apply directly to non-right triangles without first having to create right triangles.

Any triangle that is not a right triangle is an oblique triangle. Solving an oblique triangle means finding the measurements of all three angles and all three sides. To do so, we need to start with at least three of these values, including at least one of the sides. We will investigate three possible oblique triangle problem situations:

ASA (angle-side-angle) We know the measurements of two angles and the included side. See Figure 2.

Figure 2
AAS (angle-angle-side) We know the measurements of two angles and a side that is not between the known angles. See Figure 3.

Figure 3
SSA (side-side-angle) We know the measurements of two sides and an angle that is not between the known sides. See Figure 4.

Figure 4

Knowing how to approach each of these situations enables us to solve oblique triangles without having to drop a perpendicular to form two right triangles. Instead, we can use the fact that the ratio of the measurement of one of the angles to the length of its opposite side will be equal to the other two ratios of angle measure to opposite side. Let’s see how this statement is derived by considering the triangle shown in Figure 5.

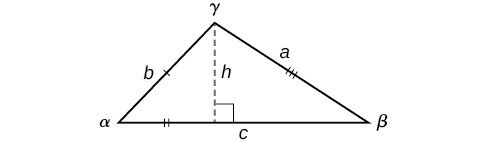
An oblique triangle consisting of sides a, b, and c, and angles alpha, beta, and gamma. Side c is opposide angle gamma and is the horizontal base of the triangle. Side b is opposite angle beta, and side a is opposite angle alpha. There is a dotted perpendicular line - an altitude - from the gamma angle to the horizontal base c.

Figure 5

Using the right triangle relationships, we know that $\sin \alpha =\frac{h}{b}$ and $\sin \beta =\frac{h}{a}$ . Solving both equations for $h$ gives two different expressions for $h$ .

h = b sin α and h = a sin β

$h=b\sin \alpha \text{ and }h=a\sin \beta$

We then set the expressions equal to each other.

\begin{matrix} b sin α = a sin β (\frac{1}{a b}) (b sin α) = (a sin β) (\frac{1}{a b}) \begin{matrix} \end{matrix} & Multiply both sides by \frac{1}{a b} . \frac{sin α}{a} = \frac{sin β}{b} \end{matrix}

$\begin{array}{ll}\text{ }b\sin \alpha =a\sin \beta \hfill & \hfill \\ \text{ }\left(\frac{1}{ab}\right)\left(b\sin \alpha \right)=\left(a\sin \beta \right)\left(\frac{1}{ab}\right)\begin{array}{cccc}& & & \end{array}\hfill & \text{Multiply both sides by}\frac{1}{ab}. \hfill \\ \text{ }\frac{\sin \alpha }{a}=\frac{\sin \beta }{b}\hfill & \hfill \end{array}$

Similarly, we can compare the other ratios.

\frac{sin α}{a} = \frac{sin γ}{c} and \frac{sin β}{b} = \frac{sin γ}{c}

$\frac{\sin \alpha }{a}=\frac{\sin \gamma }{c}\text{ and }\frac{\sin \beta }{b}=\frac{\sin \gamma }{c}$

Collectively, these relationships are called the Law of Sines.

\frac{sin α}{a} = \frac{sin β}{b} = \frac{sin λ}{c}

$\frac{\sin \alpha }{a}=\frac{\sin \beta }{b}=\frac{\sin \lambda }{c}$

Note the standard way of labeling triangles: angle $\alpha$ (alpha) is opposite side $a$ ; angle $\beta$ (beta) is opposite side $b$ ; and angle $\gamma$ (gamma) is opposite side $c$ . See Figure 6.

While calculating angles and sides, be sure to carry the exact values through to the final answer. Generally, final answers are rounded to the nearest tenth, unless otherwise specified.

Figure 6

A General Note: Law of Sines

Given a triangle with angles and opposite sides labeled as in Figure 6, the ratio of the measurement of an angle to the length of its opposite side will be equal to the other two ratios of angle measure to opposite side. All proportions will be equal. The Law of Sines is based on proportions and is presented symbolically two ways.

\frac{sin α}{a} = \frac{sin β}{b} = \frac{sin γ}{c}

$\frac{\sin \alpha }{a}=\frac{\sin \beta }{b}=\frac{\sin \gamma }{c}$

\frac{a}{sin α} = \frac{b}{sin β} = \frac{c}{sin γ}

$\frac{a}{\sin \alpha }=\frac{b}{\sin \beta }=\frac{c}{\sin \gamma }$

To solve an oblique triangle, use any pair of applicable ratios.

Example 1: Solving for Two Unknown Sides and Angle of an AAS Triangle

Solve the triangle shown in Figure 7 to the nearest tenth.

An oblique triangle with standard labels. Angle alpha is 50 degrees, angle gamma is 30 degrees, and side a is of length 10. Side b is the horizontal base.

Figure 7

Solution

The three angles must add up to 180 degrees. From this, we can determine that

\begin{matrix} \begin{matrix} β = 180^{\circ} - 50^{\circ} - 30^{\circ} \end{matrix} = 100^{\circ} \end{matrix}

$\begin{array}{l}\begin{array}{l}\hfill \\ \beta =180^\circ -50^\circ -30^\circ \hfill \end{array}\hfill \\ =100^\circ \hfill \end{array}$

To find an unknown side, we need to know the corresponding angle and a known ratio. We know that angle $\alpha =50^\circ$ and its corresponding side $a=10$ . We can use the following proportion from the Law of Sines to find the length of $c$ .

\begin{matrix} \frac{sin (50^{\circ})}{10} = \frac{sin (30^{\circ})}{c} c \frac{sin (50^{\circ})}{10} = sin (30^{\circ}) & Multiply both sides by c . c = sin (30^{\circ}) \frac{10}{sin (50^{\circ})} & Multiply by the reciprocal to isolate c . c \approx 6.5 \end{matrix}

$\begin{array}{llllll}\frac{\sin \left(50^\circ \right)}{10}=\frac{\sin \left(30^\circ \right)}{c}\hfill & \hfill & \hfill & \hfill & \hfill & \hfill \\ c\frac{\sin \left(50^\circ \right)}{10}=\sin \left(30^\circ \right)\hfill & \hfill & \hfill & \hfill & \hfill & \text{Multiply both sides by }c.\hfill \\ c=\sin \left(30^\circ \right)\frac{10}{\sin \left(50^\circ \right)}\hfill & \hfill & \hfill & \hfill & \hfill & \text{Multiply by the reciprocal to isolate }c.\hfill \\ c\approx 6.5\hfill & \hfill & \hfill & \hfill & \hfill & \hfill \end{array}$

Similarly, to solve for $b$ , we set up another proportion.

\begin{matrix} \begin{matrix} \frac{sin (50^{\circ})}{10} = \frac{sin (100^{\circ})}{b} \end{matrix} b sin (50^{\circ}) = 10 sin (100^{\circ}) & Multiply both sides by b . b = \frac{10 sin (100^{\circ})}{sin (50^{\circ})} \begin{matrix} \end{matrix} & Multiply by the reciprocal to isolate b . b \approx 12.9 \end{matrix}

$\begin{array}{ll}\begin{array}{l}\hfill \\ \text{ }\frac{\sin \left(50^\circ \right)}{10}=\frac{\sin \left(100^\circ \right)}{b}\hfill \end{array}\hfill & \hfill \\ \text{ }b\sin \left(50^\circ \right)=10\sin \left(100^\circ \right)\hfill & \text{Multiply both sides by }b.\hfill \\ \text{ }b=\frac{10\sin \left(100^\circ \right)}{\sin \left(50^\circ \right)}\begin{array}{cccc}& & & \end{array}\hfill & \text{Multiply by the reciprocal to isolate }b.\hfill \\ \text{ }b\approx 12.9\hfill & \hfill \end{array}$

Therefore, the complete set of angles and sides is

\begin{matrix} \begin{matrix} α = 50^{\circ} a = 10 \end{matrix} β = 100^{\circ} b \approx 12.9 γ = 30^{\circ} c \approx 6.5 \end{matrix}

$\begin{array}{l}\begin{array}{l}\hfill \\ \alpha =50^\circ a=10\hfill \end{array}\hfill \\ \beta =100^\circ b\approx 12.9\hfill \\ \gamma =30^\circ c\approx 6.5\hfill \end{array}$

Try It 1

Solve the triangle shown in Figure 8 to the nearest tenth.

An oblique triangle with standard labels. Angle alpha is 98 degrees, angle gamma is 43 degrees, and side b is of length 22. Side b is the horizontal base.

Figure 8

Solution

Using The Law of Sines to Solve SSA Triangles

We can use the Law of Sines to solve any oblique triangle, but some solutions may not be straightforward. In some cases, more than one triangle may satisfy the given criteria, which we describe as an ambiguous case. Triangles classified as SSA, those in which we know the lengths of two sides and the measurement of the angle opposite one of the given sides, may result in one or two solutions, or even no solution.

A General Note: Possible Outcomes for SSA Triangles

Oblique triangles in the category SSA may have four different outcomes. Figure 9 illustrates the solutions with the known sides $a$ and $b$ and known angle $\alpha$ .

Four attempted oblique triangles are in a row, all with standard labels. Side c is the horizontal base. In the first attempted triangle, side a is less than the altitude height. Since side a cannot reach side c, there is no triangle. In the second attempted triangle, side a is equal to the length of the altitude height, so side a forms a right angle with side c. In the third attempted triangle, side a is greater than the altitude height and less than side b, so side a can form either an acute or obtuse angle with side c. In the fourth attempted triangle, side a is greater than or equal to side b, so side a forms an acute angle with side c.

Figure 9

Example 1: Solving an Oblique SSA Triangle

Solve the triangle in Figure 10 for the missing side and find the missing angle measures to the nearest tenth.

An oblique triangle with standard labels where side a is of length 6, side b is of length 8, and angle alpha is 35 degrees.

Figure 10

Solution

Use the Law of Sines to find angle $\beta$ and angle $\gamma$ , and then side $c$ . Solving for $\beta$ , we have the proportion

\begin{matrix} \frac{sin α}{a} = \frac{sin β}{b} \frac{sin (35^{\circ})}{6} = \frac{sin β}{8} \frac{8 sin (35^{\circ})}{6} = sin β 0.7648 \approx sin β {sin}^{- 1} (0.7648) \approx {49.9}^{\circ} β \approx {49.9}^{\circ} \end{matrix}

$\begin{array}{r}\hfill \frac{\sin \alpha }{a}=\frac{\sin \beta }{b}\\ \hfill \frac{\sin \left(35^\circ \right)}{6}=\frac{\sin \beta }{8}\\ \hfill \frac{8\sin \left(35^\circ \right)}{6}=\sin \beta \\ \hfill 0.7648\approx \sin \beta \\ \hfill {\sin }^{-1}\left(0.7648\right)\approx 49.9^\circ \\ \hfill \beta \approx 49.9^\circ \end{array}$

However, in the diagram, angle $\beta$ appears to be an obtuse angle and may be greater than 90°. How did we get an acute angle, and how do we find the measurement of $\beta ?$ Let’s investigate further. Dropping a perpendicular from $\gamma$ and viewing the triangle from a right angle perspective, we have Figure 11. It appears that there may be a second triangle that will fit the given criteria.

An oblique triangle built from the previous with standard prime labels. Side a is of length 6, side b is of length 8, and angle alpha prime is 35 degrees. An isosceles triangle is attached, using side a as one of its congruent legs and the angle supplementary to angle beta as one of its congruent base angles. The other congruent angle is called beta prime, and the entire new horizontal base, which extends from the original side c, is called c prime. There is a dotted altitude line from angle gamma prime to side c prime.

Figure 11

The angle supplementary to $\beta$ is approximately equal to 49.9°, which means that $\beta =180^\circ -49.9^\circ =130.1^\circ$ . (Remember that the sine function is positive in both the first and second quadrants.) Solving for $\gamma$ , we have

γ = 180^{\circ} - 35^{\circ} - {130.1}^{\circ} \approx {14.9}^{\circ}

$\gamma =180^\circ -35^\circ -130.1^\circ \approx 14.9^\circ$

We can then use these measurements to solve the other triangle. Since ${\gamma }^{\prime }$ is supplementary to $\gamma$ , we have

γ^{'} = 180^{\circ} - 35^{\circ} - {49.9}^{\circ} \approx {95.1}^{\circ}

${\gamma }^{\prime }=180^\circ -35^\circ -49.9^\circ \approx 95.1^\circ$

Now we need to find $c$ and ${c}^{\prime }$ .

We have

\begin{matrix} \frac{c}{sin ({14.9}^{\circ})} = \frac{6}{sin (35^{\circ})} c = \frac{6 sin ({14.9}^{\circ})}{sin (35^{\circ})} \approx 2.7 \end{matrix}

$\begin{array}{l}\frac{c}{\sin \left(14.9^\circ \right)}=\frac{6}{\sin \left(35^\circ \right)}\hfill \\ \text{ }c=\frac{6\sin \left(14.9^\circ \right)}{\sin \left(35^\circ \right)}\approx 2.7\hfill \end{array}$

Finally,

\begin{matrix} \frac{c^{'}}{sin ({95.1}^{\circ})} = \frac{6}{sin (35^{\circ})} c^{'} = \frac{6 sin ({95.1}^{\circ})}{sin (35^{\circ})} \approx 10.4 \end{matrix}

$\begin{array}{l}\frac{{c}^{\prime }}{\sin \left(95.1^\circ \right)}=\frac{6}{\sin \left(35^\circ \right)}\hfill \\ \text{ }{c}^{\prime }=\frac{6\sin \left(95.1^\circ \right)}{\sin \left(35^\circ \right)}\approx 10.4\hfill \end{array}$

To summarize, there are two triangles with an angle of 35°, an adjacent side of 8, and an opposite side of 6, as shown in Figure 12.

There are two triangles with standard labels. Triangle a is the orginal triangle. It has angles alpha of 35 degrees, beta of 130.1 degrees, and gamma of 14.9 degrees. It has sides a = 6, b = 8, and c is approximately 2.7. Triangle b is the extended triangle. It has angles alpha prime = 35 degrees, angle beta prime = 49.9 degrees, and angle gamma prime = 95.1 degrees. It has side a prime = 6, side b prime = 8, and side c prime is approximately 10.4.

Figure 12

However, we were looking for the values for the triangle with an obtuse angle $\beta$ . We can see them in the first triangle (a) in Figure 12.

Try It 2

Given $\alpha =80^\circ ,a=120$ , and $b=121$ , find the missing side and angles. If there is more than one possible solution, show both.

Solution

Example 2: Solving for the Unknown Sides and Angles of a SSA Triangle

In the triangle shown in Figure 13, solve for the unknown side and angles. Round your answers to the nearest tenth.

An oblique triangle with standard labels. Side b is 9, side c is 12, and angle gamma is 85. Angle alpha, angle beta, and side a are unknown.

Figure 13

Solution

In choosing the pair of ratios from the Law of Sines to use, look at the information given. In this case, we know the angle $\gamma =85^\circ$ , and its corresponding side $c=12$ , and we know side $b=9$ . We will use this proportion to solve for $\beta$ .

\begin{matrix} \frac{sin (85^{\circ})}{12} = \frac{sin β}{9} \begin{matrix} \end{matrix} & Isolate the unknown . \frac{9 sin (85^{\circ})}{12} = sin β \end{matrix}

$\begin{array}{ll}\frac{\sin \left(85^\circ \right)}{12}=\frac{\sin \beta }{9}\begin{array}{cccc}& & & \end{array}\hfill & \text{Isolate the unknown}.\hfill \\ \frac{9\sin \left(85^\circ \right)}{12}=\sin \beta \hfill & \hfill \end{array}$

To find $\beta$ , apply the inverse sine function. The inverse sine will produce a single result, but keep in mind that there may be two values for $\beta$ . It is important to verify the result, as there may be two viable solutions, only one solution (the usual case), or no solutions.

\begin{matrix} β = {sin}^{- 1} (\frac{9 sin (85^{\circ})}{12}) β \approx {sin}^{- 1} (0.7471) β \approx {48.3}^{\circ} \end{matrix}

$\begin{array}{l}\beta ={\sin }^{-1}\left(\frac{9\sin \left(85^\circ \right)}{12}\right)\hfill \\ \beta \approx {\sin }^{-1}\left(0.7471\right)\hfill \\ \beta \approx 48.3^\circ \hfill \end{array}$

In this case, if we subtract $\beta$ from 180°, we find that there may be a second possible solution. Thus, $\beta =180^\circ -48.3^\circ \approx 131.7^\circ$ . To check the solution, subtract both angles, 131.7° and 85°, from 180°. This gives

α = 180^{\circ} - 85^{\circ} - {131.7}^{\circ} \approx - {36.7}^{\circ}

$\alpha =180^\circ -85^\circ -131.7^\circ \approx -36.7^\circ$ ,

which is impossible, and so $\beta \approx 48.3^\circ$ .

To find the remaining missing values, we calculate $\alpha =180^\circ -85^\circ -48.3^\circ \approx 46.7^\circ$ . Now, only side $a$ is needed. Use the Law of Sines to solve for $a$ by one of the proportions.

\begin{matrix} \begin{matrix} \begin{matrix} \frac{sin (85^{\circ})}{12} = \frac{sin ({46.7}^{\circ})}{a} \end{matrix} \end{matrix} a \frac{sin (85^{\circ})}{12} = sin ({46.7}^{\circ}) a = \frac{12 sin ({46.7}^{\circ})}{sin (85^{\circ})} \approx 8.8 \end{matrix}

$\begin{array}{l}\begin{array}{l}\hfill \\ \begin{array}{l}\hfill \\ \frac{\sin \left(85^\circ \right)}{12}=\frac{\sin \left(46.7^\circ \right)}{a}\hfill \end{array}\hfill \end{array}\hfill \\ a\frac{\sin \left(85^\circ \right)}{12}=\sin \left(46.7^\circ \right)\hfill \\ \text{ }a=\frac{12\sin \left(46.7^\circ \right)}{\sin \left(85^\circ \right)}\approx 8.8\hfill \end{array}$

The complete set of solutions for the given triangle is

\begin{matrix} \begin{matrix} α \approx {46.7}^{\circ} a \approx 8.8 \end{matrix} β \approx {48.3}^{\circ} b = 9 γ = 85^{\circ} c = 12 \end{matrix}

$\begin{array}{l}\begin{array}{l}\hfill \\ \alpha \approx 46.7^\circ \text{ }a\approx 8.8\hfill \end{array}\hfill \\ \beta \approx 48.3^\circ \text{ }b=9\hfill \\ \gamma =85^\circ \text{ }c=12\hfill \end{array}$

Try It 3

Given $\alpha =80^\circ ,a=100,b=10$ , find the missing side and angles. If there is more than one possible solution, show both. Round your answers to the nearest tenth.

Solution

Example 3: Finding the Triangles That Meet the Given Criteria

Find all possible triangles if one side has length 4 opposite an angle of 50°, and a second side has length 10.

Solution

Using the given information, we can solve for the angle opposite the side of length 10.

\begin{matrix} \frac{sin α}{10} = \frac{sin (50^{\circ})}{4} sin α = \frac{10 sin (50^{\circ})}{4} sin α \approx 1.915 \end{matrix}

$\begin{array}{l}\frac{\sin \alpha }{10}=\frac{\sin \left(50^\circ \right)}{4}\hfill \\ \sin \alpha =\frac{10\sin \left(50^\circ \right)}{4}\hfill \\ \sin \alpha \approx 1.915\hfill \end{array}$

An incomplete triangle. One side has length 4 opposite a 50 degree angle, and a second side has length 10 opposite angle a. The side of length 4 is too short to reach the side of length 10, so there is no third angle.

Figure 14

We can stop here without finding the value of $\alpha$ . Because the range of the sine function is $\left[-1,1\right]$ , it is impossible for the sine value to be 1.915. In fact, inputting ${\sin }^{-1}\left(1.915\right)$ in a graphing calculator generates an ERROR DOMAIN. Therefore, no triangles can be drawn with the provided dimensions.

Try It 4

Determine the number of triangles possible given $a=31,b=26,\beta =48^\circ$ .

Solution

Module 13: Non-Right Triangles

A General Note: Law of Sines

Example 1: Solving for Two Unknown Sides and Angle of an AAS Triangle

Solution

Try It 1

Using The Law of Sines to Solve SSA Triangles

A General Note: Possible Outcomes for SSA Triangles

Example 1: Solving an Oblique SSA Triangle

Solution

Try It 2

Example 2: Solving for the Unknown Sides and Angles of a SSA Triangle

Solution

Try It 3

Example 3: Finding the Triangles That Meet the Given Criteria

Solution

Try It 4

Candela Citations