Section 1.2: Circles

Learning Outcomes

  • Write the equation of a circle in standard form
  • Graph a circle

DEFINITION OF A CIRCLE

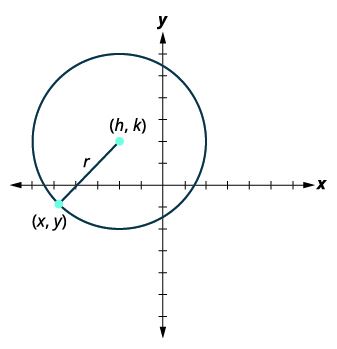
A circle is all points in a plane that are a fixed distance from a given point in the plane.  The given point is called the center, [latex](h,k)[/latex], and the fixed distance is called the radius, [latex]r[/latex], of the circle.

Picture of a Circle with center marked as (h,k) and radius r

DERIVING THE STANDARD FORM OF A CIRCLE

To derive the equation of a circle, we can use the distance formula with the points [latex](h,k)[/latex], [latex](x,y)[/latex], and the distance [latex]r[/latex].

[latex]d=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}[/latex]

Substitute the values.

[latex]r=\sqrt{(x-h)^{2}+(y-k)^{2}}[/latex]

Square both sides.

[latex]r^{2}=(x-h)^{2}+(y-k)^{2}[/latex]

 

STANDARD FORM OF A CIRCLE

The standard form of a circle is as follows:

[latex]{\left(x-h\right)}^{2}+{\left(y-k\right)}^{2}=r^{2}[/latex]

Write the Equation of a Circle in Standard Form

Example 1: WRITE THE STANDARD FORM Equation OF A CIRCLE

Write the standard form of a circle with radius [latex]3[/latex] and center [latex](0,0)[/latex].

 

Use the standard form of a circle.

[latex]{\left(x-h\right)}^{2}+{\left(y-k\right)}^{2}=r^{2}[/latex]

Substitute in the values [latex]r=3, h=0, k=0[/latex].

  [latex]{\left(x-0\right)}^{2}+{\left(y-0\right)}^{2}=3^{2}[/latex]

Simplify.

[latex]{x}^{2}+{y}^{2}=9[/latex]

 

Example 2: WRITE THE STANDARD FORM equation OF A CIRCLE

Write the standard form of a circle with radius [latex]2[/latex] and center [latex](-1,3)[/latex].

Example 3: finding the center and radius

Find the center and radius, then graph the circle: [latex]{\left(x+2\right)}^{2}+{\left(y-1\right)}^{2}=9[/latex].

 

Use the standard form of a circle.

[latex]{\left(x-h\right)}^{2}+{\left(y-k\right)}^{2}=r^{2}[/latex]

Identify the center [latex](h,k)[/latex], and radius [latex]r[/latex].

  [latex]{\left(x-(-2)\right)}^{2}+{\left(y-1\right)}^{2}=3^{2}[/latex]

The center is [latex](-2,1)[/latex], and the radius is [latex]3[/latex].

 

Now graph the circle.  Plot the center first and then go up, down, left, and right 2 places.

Graph of a Circle with center (-2,1) and radius 3

Example 4: finding the center and radius

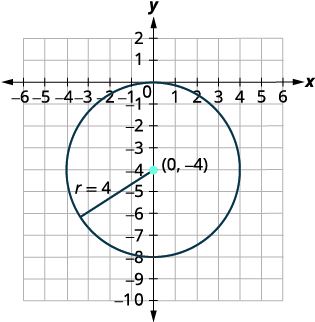
Find the center and radius, then graph the circle: [latex]{4x}^{2}+{4y}^{2}=64[/latex].

GENERAL FORM OF A CIRCLE

The general form of a circle is as follows:

[latex]{x}^{2}+{y}^{2}+ax+by+c=0[/latex]

Example 5: WRITE THE STANDARD FORM Equation OF A CIRCLE

Find the center and radius, then graph: [latex]{x}^{2}+{y}^{2}-4x-6y+4=0[/latex].

We need to rewrite this general form into standard form in order to find the center and radius.

[latex]{x}^{2}+{y}^{2}-4x-6y+4=0[/latex]

 

Group the x-terms and y-terms.  Collect the constants on the right right side.

  [latex]{x}^{2}-4x+{y}^{2}-6y=-4[/latex]

Complete the squares.

[latex]{x}^{2}-4x+4+{y}^{2}-6y+9=-4+4+9[/latex]

Rewrite as binomial squares.

[latex]{\left(x-2\right)}^{2}+{\left(y-3\right)}^{2}=9[/latex]

 

The center is [latex](2,3)[/latex], and the radius is [latex]3[/latex].

 

Now graph the circle.  Plot the center first and then go up, down, left, and right 3 places.

Graph of a Circle with center centered at (2,3) and radius 3

Example 6: WRITE THE STANDARD FORM Equation OF A CIRCLE

Find the center and radius, then graph: [latex]{x}^{2}+{y}^{2}+8y=0[/latex].

Example 7: APPLYING THE DISTANCE AND MIDPOINT FORMULAS TO A CIRCLE EQUATION

The diameter of a circle has endpoints [latex](-1,-4)[/latex] and [latex](7,2)[/latex]. Find the center and radius of the circle and also write its standard form equation.

The center of a circle is the center, or midpoint, of its diameter.  Thus the midpoint formula will yield the center point.

 

[latex]M=\left(\frac{{x}_{1}+{x}_{2}}{2},\frac{{y}_{1}+{y}_{2}}{2}\right)[/latex]

  [latex]=\left(\frac{-1+7}{2},\frac{-4+2}{2}\right)[/latex]

[latex]=\left(\frac{6}{2},\frac{-2}{2}\right)[/latex]

[latex]=(3,-1)[/latex]

 

The center is [latex](3,-1)[/latex].  The distance formula will be used to find the distance from the center to one of the points on the circle.  This will yield the radius:

 

[latex]d=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}[/latex]

[latex]d=\sqrt{(7-3)^{2}+(2-(-1))^{2}}[/latex]

[latex]d=\sqrt{4^{2}+3^{2}}=5[/latex]

 

The distance from the center to a point on the circle is 5.  Therefore the radius is 5.  The center and radius can now be used to find the standard form of the circle:

 

Start with the standard form of a circle.

[latex]{\left(x-h\right)}^{2}+{\left(y-k\right)}^{2}=r^{2}[/latex]

Substitute in the values [latex]r=5, h=3, k=-1[/latex].

  [latex]{\left(x-3\right)}^{2}+{\left(y-(-1)\right)}^{2}=5^{2}[/latex]

Simplify.

[latex]{\left(x-3\right)}^{2}+{\left(y+1\right)}^{2}=25[/latex]

 

 

Example 8: Finding the Center of a Circle

The diameter of a circle has endpoints [latex]\left(-1,-4\right)[/latex] and [latex]\left(5,-4\right)[/latex]. Find the center of the circle.

Key Concepts

  • A circle is all points in a plane that are a fixed distance from a given point on the plane.  The given point is called the center, and the fixed distance is called the radius.
  • The standard form of the equation of a circle with center [latex](h,k)[/latex] and radius [latex]r[/latex] is [latex]{\left(x-h\right)}^{2}{+}{\left(y-k\right)}^{2}=r^{2}[/latex]

Section 1.2 Homework Exercises

For the following exercises, write the standard form of the equation of the circle with the given radius and center [latex](0,0)[/latex].

1. Radius: [latex]7[/latex]

2. Radius: [latex]9[/latex]

3. Radius: [latex]\sqrt{2}[/latex]

4. Radius: [latex]\sqrt{5}[/latex]

In the following exercises, write the standard form of the equation of the circle with the given radius and center.

5. Radius: [latex]1[/latex], center: [latex](3,5)[/latex]

6. Radius: [latex]10[/latex], center: [latex](-2,6)[/latex]

7. Radius: [latex]2.5[/latex], center: [latex](1.5,-3.5)[/latex]

8. Radius: [latex]1.5[/latex], center: [latex](-5.5,-6.5)[/latex]

For the following exercises, write the standard form of the equation of the circle with the given center and point on the circle.

9. Center: [latex](3,-2)[/latex] with point [latex](3,6)[/latex]

10. Center: [latex](6,-6)[/latex] with point [latex](2,-3)[/latex]

11. Center: [latex](4,4)[/latex] with point [latex](2,2)[/latex]

12. Center: [latex](-5,6)[/latex] with point [latex](-2,3)[/latex]

In the following exercises, find the center and radius and then graph each circle.

13. [latex]{\left(x+5\right)}^{2}+{\left(y+3\right)}^{2}=1[/latex]

14. [latex]{\left(x-2\right)}^{2}+{\left(y-3\right)}^{2}=9[/latex]

15. [latex]{\left(x-4\right)}^{2}+{\left(y+2\right)}^{2}=16[/latex]

16. [latex]{\left(x+2\right)}^{2}+{\left(y-5\right)}^{2}=4[/latex]

17. [latex]x^{2}+{\left(y+2\right)}^{2}=25[/latex]

18. [latex]{\left(x-1\right)}^{2}+{y}^{2}=36[/latex]

19. [latex]{\left(x-1.5\right)}^{2}+{\left(y-2.5\right)}^{2}=0.25[/latex]

20. [latex]{\left(x-1\right)}^{2}+{\left(y-3\right)}^{2}=\frac{9}{4}[/latex]

21. [latex]x^{2}+y^{2}=64[/latex]

22. [latex]x^{2}+y^{2}=49[/latex]

23. [latex]2x^{2}+2y^{2}=8[/latex]

24. [latex]6x^{2}+6y^{2}=216[/latex]

In the following exercises, identify the center and radius and graph.

25. [latex]x^{2}+y^{2}+2x+6y+9=0[/latex]

26. [latex]x^{2}+y^{2}-6x-8y=0[/latex]

27. [latex]x^{2}+y^{2}-4x+10y-7=0[/latex]

28. [latex]x^{2}+y^{2}+12x-14y+21=0[/latex]

29. [latex]x^{2}+y^{2}+6y+5=0[/latex]

30. [latex]x^{2}+y^{2}-10y=0[/latex]

31. [latex]x^{2}+y^{2}+4x=0[/latex]

32. [latex]x^{2}+y^{2}-14x+13=0[/latex]

33. Explain the relationship between the distance formula and the equation of a circle.

34. In your own words, state the definition of a circle.

35. In your own words, explain the steps you would take to change the general form of the equation of a circle to the standard form.