Figure 1. Electron micrograph of E.Coli bacteria (credit: “Mattosaurus,” Wikimedia Commons)
Focus in on a square centimeter of your skin. Look closer. Closer still. If you could look closely enough, you would see hundreds of thousands of microscopic organisms. They are bacteria, and they are not only on your skin, but in your mouth, nose, and even your intestines. In fact, the bacterial cells in your body at any given moment outnumber your own cells. But that is no reason to feel bad about yourself. While some bacteria can cause illness, many are healthy and even essential to the body.
Bacteria commonly reproduce through a process called binary fission, during which one bacterial cell splits into two. When conditions are right, bacteria can reproduce very quickly. Unlike humans and other complex organisms, the time required to form a new generation of bacteria is often a matter of minutes or hours, as opposed to days or years.[1]
For simplicity’s sake, suppose we begin with a culture of one bacterial cell that can divide every hour. The table below shows the number of bacterial cells at the end of each subsequent hour. We see that the single bacterial cell leads to over one thousand bacterial cells in just ten hours! And if we were to extrapolate the table to twenty-four hours, we would have over 16 million!
| Hour | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Bacteria | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
Exponential Functions
In this chapter, we will explore exponential functions, which can be used for, among other things, modeling growth patterns such as those found in bacteria. We will also investigate logarithmic functions, which are closely related to exponential functions. Both types of functions have numerous real-world applications when it comes to modeling and interpreting data.
Learning Outcomes
- Review Laws of Exponents
- Evaluate exponential functions.
- Find the equation of an exponential function.
- Use compound interest formulas.
- Evaluate exponential functions with base e.
- Graph exponential functions
- Graph exponential functions using transformations.
India is the second most populous country in the world with a population of about 1.25 billion people in 2013. The population is growing at a rate of about 1.2% each year.[2] If this rate continues, the population of India will exceed China’s population by the year 2031. When populations grow rapidly, we often say that the growth is “exponential,” meaning that something is growing very rapidly. To a mathematician, however, the term exponential growth has a very specific meaning. In this section, we will take a look at exponential functions, which model this kind of rapid growth.
First, we will briefly review laws of exponents.
The Product Rule for Exponents
For any number a and any integers n and m, [latex]\left(a^{n}\right)\left(a^{m}\right) = a^{n+m}[/latex].
The Quotient (Division) Rule for Exponents
For any non-zero number a and any integers n and n: [latex] \displaystyle \frac{{{a}^{n}}}{{{a}^{m}}}={{a}^{n-m}}[/latex]
The Power Rule for Exponents
For any positive number a and integers n and m: [latex]\left(a^{n}\right)^{m}=a^{n\cdot{m}}[/latex].
Take a moment to contrast how this is different from the product rule for exponents.
A Product Raised to a Power
For any nonzero numbers a and b and any integer n, [latex]\left(ab\right)^{n}=a^{n}\cdot{b^{n}}[/latex].
A Quotient Raised to a Power
For any number a, any non-zero number b, and any integer n, [latex] \displaystyle {\left(\frac{a}{b}\right)}^{n}=\frac{a^{n}}{b^{n}}[/latex].
Exponents of 0 or 1
Any number or variable raised to a power of 1 is the number itself.
[latex]a^{1}=a[/latex]
Any non-zero number or variable raised to a power of 0 is equal to 1
[latex]a^{0}=1[/latex]
The quantity [latex]0^{0}[/latex] is undefined.
The Negative Rule of Exponents
For any nonzero real number [latex]a[/latex] and natural number [latex]n[/latex], the negative rule of exponents states that
and
Example 1: Practice Exponent Rules
Simplify [latex]\frac{\left(t^{3}\right)^2}{\left(t^2\right)^{-8}}[/latex]
Write your answer with positive exponents.
Example 2: Practice Exponent Rules
Simplify [latex]\frac{\left(5x\right)^{-2}y}{x^3y^{-1}}[/latex]
Write your answer with positive exponents.
Evaluate Exponential Functions
Recall that the base of an exponential function must be a positive real number other than 1. Why do we limit the base b to positive values? To ensure that the outputs will be real numbers. Observe what happens if the base is not positive:
- Let b = –9 and [latex]x=\frac{1}{2}[/latex]. Then [latex]f\left(x\right)=f\left(\frac{1}{2}\right)={\left(-9\right)}^{\frac{1}{2}}=\sqrt{-9}[/latex], which is not a real number.
Why do we limit the base to positive values other than 1? Because base 1 results in the constant function. Observe what happens if the base is 1:
- Let b = 1. Then [latex]f\left(x\right)={1}^{x}=1[/latex] for any value of x.
To evaluate an exponential function with the form [latex]f\left(x\right)={b}^{x}[/latex], we simply substitute x with the given value, and calculate the resulting power. For example:
Let [latex]f\left(x\right)={2}^{x}[/latex]. What is [latex]f\left(3\right)[/latex]?
To evaluate an exponential function with a form other than the basic form, it is important to follow the order of operations. For example:
Let [latex]f\left(x\right)=30{\left(2\right)}^{x}[/latex]. What is [latex]f\left(3\right)[/latex]?
Note that if the order of operations were not followed, the result would be incorrect:
[latex]f\left(3\right)=30{\left(2\right)}^{3}\ne {60}^{3}=216,000[/latex]
Example 3: Evaluating Exponential Functions
Let [latex]f\left(x\right)=5{\left(3\right)}^{x+1}[/latex]. Evaluate [latex]f\left(2\right)[/latex] without using a calculator.
Try It
Let [latex]f\left(x\right)=8{\left(1.2\right)}^{x - 5}[/latex]. Evaluate [latex]f\left(3\right)[/latex] using a calculator. Round to four decimal places.
Use Compound Interest Formulas
Savings instruments in which earnings are continually reinvested, such as mutual funds and retirement accounts, use compound interest. The term compounding refers to interest earned not only on the original value, but on the accumulated value of the account.
The annual percentage rate (APR) of an account, also called the nominal rate, is the yearly interest rate earned by an investment account. The term nominal is used when the compounding occurs a number of times other than once per year. In fact, when interest is compounded more than once a year, the effective interest rate ends up being greater than the nominal rate! This is a powerful tool for investing.
We can calculate the compound interest using the compound interest formula, which is an exponential function of the variables time t, principal P, APR r, and number of compounding periods in a year n:
For example, observe the table below, which shows the result of investing $1,000 at 10% for one year. Notice how the value of the account increases as the compounding frequency increases.
| Frequency | Value after 1 year |
|---|---|
| Annually | $1100 |
| Semiannually | $1102.50 |
| Quarterly | $1103.81 |
| Monthly | $1104.71 |
| Daily | $1105.16 |
A General Note: The Compound Interest Formula
Compound interest can be calculated using the formula
where
- A(t) is the account value,
- t is measured in years,
- P is the starting amount of the account, often called the principal, or more generally present value,
- r is the annual percentage rate (APR) expressed as a decimal, and
- n is the number of compounding periods in one year.
Example 4: Calculating Compound Interest
If we invest $3,000 in an investment account paying 3% interest compounded quarterly, how much will the account be worth in 10 years?
Try It
An initial investment of $100,000 at 12% interest is compounded weekly (use 52 weeks in a year). What will the investment be worth in 30 years?
Try It
Evaluate exponential functions with base e
As we saw earlier, the amount earned on an account increases as the compounding frequency increases. The table below shows that the increase from annual to semi-annual compounding is larger than the increase from monthly to daily compounding. This might lead us to ask whether this pattern will continue.
Examine the value of $1 invested at 100% interest for 1 year, compounded at various frequencies.
| Frequency | [latex]A\left(t\right)={\left(1+\frac{1}{n}\right)}^{n}[/latex] | Value |
|---|---|---|
| Annually | [latex]{\left(1+\frac{1}{1}\right)}^{1}[/latex] | $2 |
| Semiannually | [latex]{\left(1+\frac{1}{2}\right)}^{2}[/latex] | $2.25 |
| Quarterly | [latex]{\left(1+\frac{1}{4}\right)}^{4}[/latex] | $2.441406 |
| Monthly | [latex]{\left(1+\frac{1}{12}\right)}^{12}[/latex] | $2.613035 |
| Daily | [latex]{\left(1+\frac{1}{365}\right)}^{365}[/latex] | $2.714567 |
| Hourly | [latex]{\left(1+\frac{1}{\text{8766}}\right)}^{\text{8766}}[/latex] | $2.718127 |
| Once per minute | [latex]{\left(1+\frac{1}{\text{525960}}\right)}^{\text{525960}}[/latex] | $2.718279 |
| Once per second | [latex]{\left(1+\frac{1}{31557600}\right)}^{31557600}[/latex] | $2.718282 |
These values appear to be approaching a limit as n increases without bound. In fact, as n gets larger and larger, the expression [latex]{\left(1+\frac{1}{n}\right)}^{n}[/latex] approaches a number used so frequently in mathematics that it has its own name: the letter [latex]e[/latex]. This value is an irrational number, which means that its decimal expansion goes on forever without repeating.
As [latex]n[/latex] approaches infinity, the expression [latex]{\left(1+\frac{1}{n}\right)}^{n}[/latex] approaches [latex]e[/latex]. Continuous compounding occurs when [latex]n[/latex] approaches infinity. Below is the formula for continuous compounding. Notice there is an [latex]e[/latex] in the formula instead of [latex]n[/latex]. The [latex]e[/latex] on a calculator is typically above the LN button.
A General Note: continuous compounding
Continuous compounding interest can be calculated using the formula
where
- A(t) is the account value,
- t is measured in years,
- P is the starting amount of the account, often called the principal, or more generally present value,
- r is the annual percentage rate (APR) expressed as a decimal
Example 5: Calculating Continuous Compounding Interest
If we invest $3,000 in an investment account paying 3% interest compounded continuously, how much will the account be worth in 10 years?
Try It
An initial investment of $100,000 at 12% interest is compounded continuously. What will the investment be worth in 30 years?
Graph exponential functions
An exponential function has the form [latex]f\left(x\right)={b}^{x}[/latex] whose base is greater than one. We’ll use the function [latex]f\left(x\right)={2}^{x}[/latex]. Observe how the output values in the table below change as the input increases by 1.
| x | –3 | –2 | –1 | 0 | 1 | 2 | 3 |
| [latex]f\left(x\right)={2}^{x}[/latex] | [latex]\frac{1}{8}[/latex] | [latex]\frac{1}{4}[/latex] | [latex]\frac{1}{2}[/latex] | 1 | 2 | 4 | 8 |
Each output value is the product of the previous output and the base, 2. We call the base 2 the constant ratio. In fact, for any exponential function with the form [latex]f\left(x\right)=a{b}^{x}[/latex], b is the constant ratio of the function. This means that as the input increases by 1, the output value will be the product of the base and the previous output, regardless of the value of a.
Notice from the table that
- the output values are positive for all values of x;
- as x increases, the output values increase without bound; and
- as x decreases, the output values grow smaller, approaching zero.
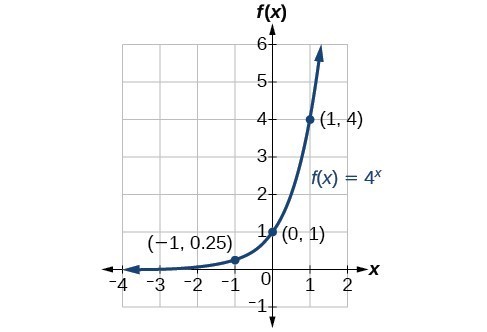
Figure 2 shows the exponential growth function [latex]f\left(x\right)={2}^{x}[/latex].
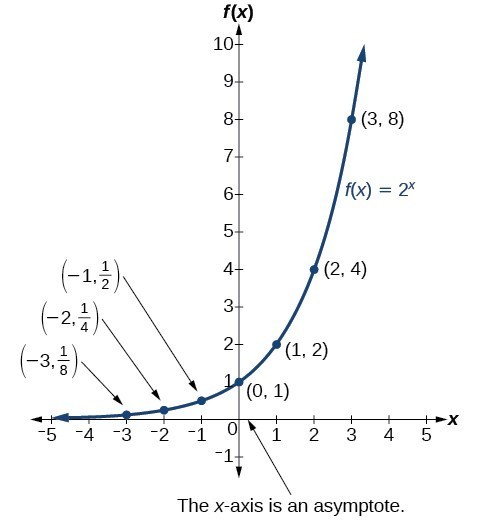
Figure 2. Notice that the graph gets close to the x-axis, but never touches it.
The domain of [latex]f\left(x\right)={2}^{x}[/latex] is all real numbers, the range is [latex]\left(0,\infty \right)[/latex], and the horizontal asymptote is [latex]y=0[/latex].
Now let’s look at an example where the base is a fraction. We can create a table of values for a function of the form [latex]f\left(x\right)={b}^{x}[/latex] whose base is between zero and one. We’ll use the function [latex]g\left(x\right)={\left(\frac{1}{2}\right)}^{x}[/latex]. Observe how the output values in the table below change as the input increases by 1.
| x | –3 | –2 | –1 | 0 | 1 | 2 | 3 |
| [latex]g\left(x\right)=\left(\frac{1}{2}\right)^{x}[/latex] | 8 | 4 | 2 | 1 | [latex]\frac{1}{2}[/latex] | [latex]\frac{1}{4}[/latex] | [latex]\frac{1}{8}[/latex] |
Again, because the input is increasing by 1, each output value is the product of the previous output and the base, or constant ratio [latex]\frac{1}{2}[/latex].
Notice from the table that
- the output values are positive for all values of x;
- as x increases, the output values grow smaller, approaching zero; and
- as x decreases, the output values grow without bound.
The graph shows the exponential decay function, [latex]g\left(x\right)={\left(\frac{1}{2}\right)}^{x}[/latex].

Figure 3. The domain of [latex]g\left(x\right)={\left(\frac{1}{2}\right)}^{x}[/latex] is all real numbers, the range is [latex]\left(0,\infty \right)[/latex], and the horizontal asymptote is [latex]y=0[/latex].
A General Note: Characteristics of the Graph of the Parent Function f(x) = bx
An exponential function with the form [latex]f\left(x\right)={b}^{x}[/latex], [latex]b>0[/latex], [latex]b\ne 1[/latex], has these characteristics:
- one-to-one function
- horizontal asymptote: [latex]y=0[/latex]
- domain: [latex]\left(-\infty , \infty \right)[/latex]
- range: [latex]\left(0,\infty \right)[/latex]
- x-intercept: none
- y-intercept: [latex]\left(0,1\right)[/latex]
- increasing if [latex]b>1[/latex]
- decreasing if [latex]b<1[/latex]
Compare the graphs of exponential growth and decay functions.

How To: Given an exponential function of the form [latex]f\left(x\right)={b}^{x}[/latex], graph the function.
- Create a table of points.
- Plot at least 3 point from the table, including the y-intercept [latex]\left(0,1\right)[/latex].
- Draw a smooth curve through the points.
- State the domain, [latex]\left(-\infty ,\infty \right)[/latex], the range, [latex]\left(0,\infty \right)[/latex], and the horizontal asymptote, [latex]y=0[/latex].
Example 6: Sketching the Graph of an Exponential Function of the Form f(x) = bx
Sketch a graph of [latex]f\left(x\right)={0.25}^{x}[/latex]. State the domain, range, and asymptote.
Try It
Sketch the graph of [latex]f\left(x\right)={4}^{x}[/latex]. State the domain, range, and asymptote.
Graph exponential functions using transformations
Transformations of exponential graphs behave similarly to those of other functions. Just as with other parent functions, we can apply the four types of transformations—shifts, reflections, stretches, and compressions—to the parent function [latex]f\left(x\right)={b}^{x}[/latex] without loss of shape. For instance, just as the quadratic function maintains its parabolic shape when shifted, reflected, stretched, or compressed, the exponential function also maintains its general shape regardless of the transformations applied.
Graphing a Vertical Shift
The first transformation occurs when we add a constant d to the parent function [latex]f\left(x\right)={b}^{x}[/latex], giving us a vertical shift d units in the same direction as the sign. For example, if we begin by graphing a parent function, [latex]f\left(x\right)={2}^{x}[/latex], we can then graph two vertical shifts alongside it, using [latex]d=3[/latex]: the upward shift, [latex]g\left(x\right)={2}^{x}+3[/latex] and the downward shift, [latex]h\left(x\right)={2}^{x}-3[/latex]. Both vertical shifts are shown in Figure 5.
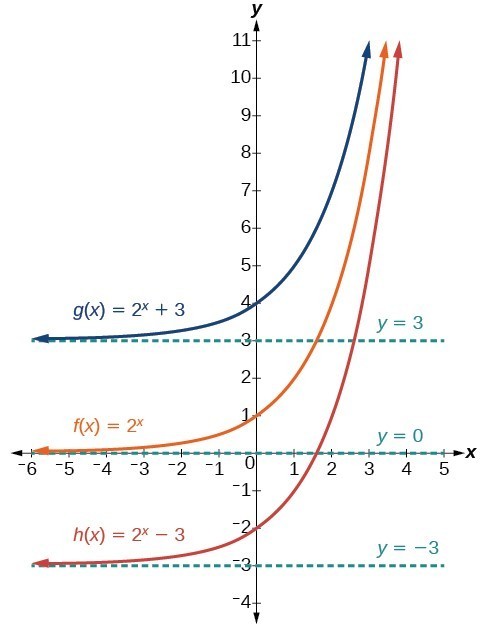
Figure 5
Observe the results of shifting [latex]f\left(x\right)={2}^{x}[/latex] vertically:
- The domain, [latex]\left(-\infty ,\infty \right)[/latex] remains unchanged.
- When the function is shifted up 3 units to [latex]g\left(x\right)={2}^{x}+3[/latex]:
- The y-intercept shifts up 3 units to [latex]\left(0,4\right)[/latex].
- The asymptote shifts up 3 units to [latex]y=3[/latex].
- The range becomes [latex]\left(3,\infty \right)[/latex].
- When the function is shifted down 3 units to [latex]h\left(x\right)={2}^{x}-3[/latex]:
- The y-intercept shifts down 3 units to [latex]\left(0,-2\right)[/latex].
- The asymptote also shifts down 3 units to [latex]y=-3[/latex].
- The range becomes [latex]\left(-3,\infty \right)[/latex].
Graphing a Horizontal Shift
The next transformation occurs when we add a constant c to the input of the parent function [latex]f\left(x\right)={b}^{x}[/latex], giving us a horizontal shift c units in the opposite direction of the sign. For example, if we begin by graphing the parent function [latex]f\left(x\right)={2}^{x}[/latex], we can then graph two horizontal shifts alongside it, using [latex]c=3[/latex]: the shift left, [latex]g\left(x\right)={2}^{x+3}[/latex], and the shift right, [latex]h\left(x\right)={2}^{x - 3}[/latex]. Both horizontal shifts are shown in Figure 6.
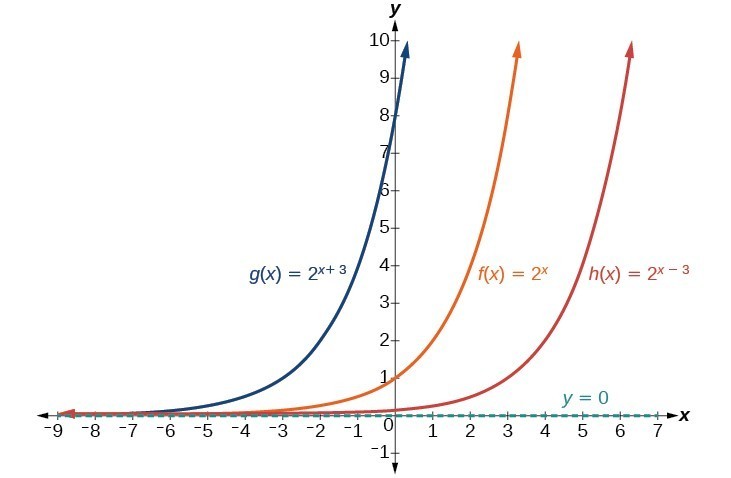
Figure 6
Observe the results of shifting [latex]f\left(x\right)={2}^{x}[/latex] horizontally:
- The domain, [latex]\left(-\infty ,\infty \right)[/latex], remains unchanged.
- The asymptote, [latex]y=0[/latex], remains unchanged.
- The y-intercept shifts such that:
- When the function is shifted left 3 units to [latex]g\left(x\right)={2}^{x+3}[/latex], the y-intercept becomes [latex]\left(0,8\right)[/latex]. This is because [latex]{2}^{x+3}=\left(8\right){2}^{x}[/latex], so the initial value of the function is 8.
- When the function is shifted right 3 units to [latex]h\left(x\right)={2}^{x - 3}[/latex], the y-intercept becomes [latex]\left(0,\frac{1}{8}\right)[/latex]. Again, see that [latex]{2}^{x - 3}=\left(\frac{1}{8}\right){2}^{x}[/latex], so the initial value of the function is [latex]\frac{1}{8}[/latex].
A General Note: Shifts of the Parent Function [latex]f\left(x\right)={b}^{x}[/latex]
For any constants c and d, the function [latex]f\left(x\right)={b}^{x+c}+d[/latex] shifts the parent function [latex]f\left(x\right)={b}^{x}[/latex]
- vertically d units, in the same direction of the sign of d.
- horizontally c units, in the opposite direction of the sign of c.
- The y-intercept becomes [latex]\left(0,{b}^{c}+d\right)[/latex].
- The horizontal asymptote becomes y = d.
- The range becomes [latex]\left(d,\infty \right)[/latex].
- The domain, [latex]\left(-\infty ,\infty \right)[/latex], remains unchanged.
How To: Given an exponential function with the form [latex]f\left(x\right)={b}^{x+c}+d[/latex], graph the translation.
- Draw the horizontal asymptote y = d.
- Identify the shift as [latex]\left(-c,d\right)[/latex]. Shift the graph of [latex]f\left(x\right)={b}^{x}[/latex] left c units if c is positive, and right [latex]c[/latex] units if c is negative.
- Shift the graph of [latex]f\left(x\right)={b}^{x}[/latex] up d units if d is positive, and down d units if d is negative.
- State the domain, [latex]\left(-\infty ,\infty \right)[/latex], the range, [latex]\left(d,\infty \right)[/latex], and the horizontal asymptote [latex]y=d[/latex].
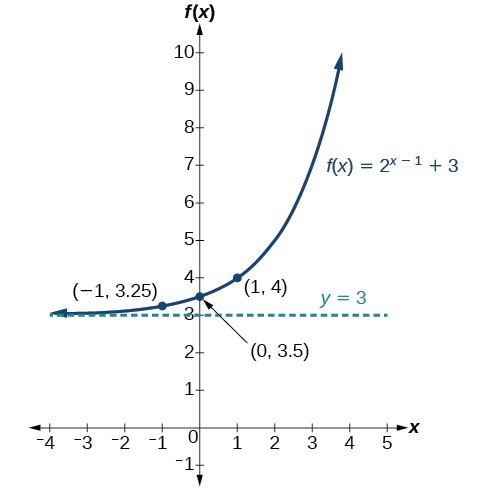
Example 7: Graphing a Shift of an Exponential Function
Graph [latex]f\left(x\right)={2}^{x+1}-3[/latex]. State the domain, range, and asymptote.
Try It
Graph [latex]f\left(x\right)={2}^{x - 1}+3[/latex]. State domain, range, and asymptote.
Try It
Graphing a Stretch or Compression
While horizontal and vertical shifts involve adding constants to the input or to the function itself, a stretch or compression occurs when we multiply the parent function [latex]f\left(x\right)={b}^{x}[/latex] by a constant [latex]|a|>0[/latex]. For example, if we begin by graphing the parent function [latex]f\left(x\right)={2}^{x}[/latex], we can then graph the stretch, using [latex]a=3[/latex], to get [latex]g\left(x\right)=3{\left(2\right)}^{x}[/latex] as shown on the left in Figure 8, and the compression, using [latex]a=\frac{1}{3}[/latex], to get [latex]h\left(x\right)=\frac{1}{3}{\left(2\right)}^{x}[/latex] as shown on the right in Figure 8.

Figure 8. (a) [latex]g\left(x\right)=3{\left(2\right)}^{x}[/latex] stretches the graph of [latex]f\left(x\right)={2}^{x}[/latex] vertically by a factor of 3. (b) [latex]h\left(x\right)=\frac{1}{3}{\left(2\right)}^{x}[/latex] compresses the graph of [latex]f\left(x\right)={2}^{x}[/latex] vertically by a factor of [latex]\frac{1}{3}[/latex].
A General Note: Stretches and Compressions of the Parent Function f(x) = bx
For any factor a > 0, the function [latex]f\left(x\right)=a{\left(b\right)}^{x}[/latex]
- is stretched vertically by a factor of a if [latex]|a|>1[/latex].
- is compressed vertically by a factor of a if [latex]|a|<1[/latex].
- has a y-intercept of [latex]\left(0,a\right)[/latex].
- has a horizontal asymptote at [latex]y=0[/latex], a range of [latex]\left(0,\infty \right)[/latex], and a domain of [latex]\left(-\infty ,\infty \right)[/latex], which are unchanged from the parent function.
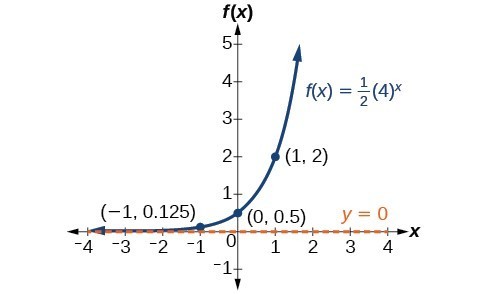
Example 8: Graphing the Stretch of an Exponential Function
Sketch a graph of [latex]f\left(x\right)=4{\left(\frac{1}{2}\right)}^{x}[/latex]. State the domain, range, and asymptote.
Try It
Sketch the graph of [latex]f\left(x\right)=\frac{1}{2}{\left(4\right)}^{x}[/latex]. State the domain, range, and asymptote.
Try It
Graphing Reflections
In addition to shifting, compressing, and stretching a graph, we can also reflect it about the x-axis or the y-axis. When we multiply the parent function [latex]f\left(x\right)={b}^{x}[/latex] by –1, we get a reflection about the x-axis. When we multiply the input by –1, we get a reflection about the y-axis. For example, if we begin by graphing the parent function [latex]f\left(x\right)={2}^{x}[/latex], we can then graph the two reflections alongside it. The reflection about the x-axis, [latex]g\left(x\right)={-2}^{x}[/latex], is shown on the left side, and the reflection about the y-axis [latex]h\left(x\right)={2}^{-x}[/latex], is shown on the right side.
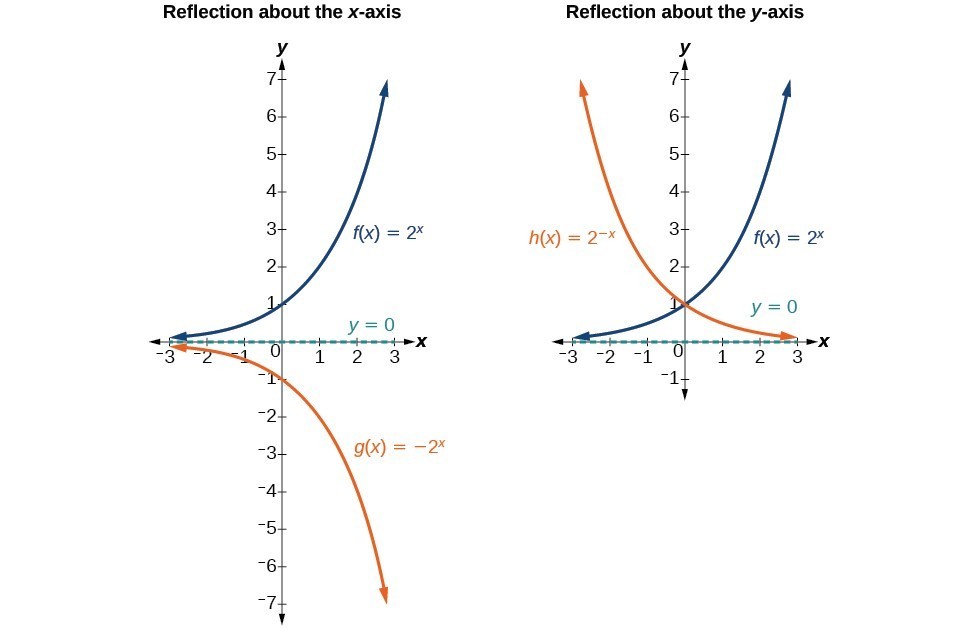
(a) [latex]g\left(x\right)=-{2}^{x}[/latex] reflects the graph of [latex]f\left(x\right)={2}^{x}[/latex] about the x-axis.
(b) [latex]g\left(x\right)={2}^{-x}[/latex] reflects the graph of [latex]f\left(x\right)={2}^{x}[/latex] about the y-axis.
A General Note: Reflections of the Parent Function f(x) = bx
The function [latex]f\left(x\right)=-{b}^{x}[/latex]
- reflects the parent function [latex]f\left(x\right)={b}^{x}[/latex] about the x-axis.
- has a y-intercept of [latex]\left(0,-1\right)[/latex].
- has a range of [latex]\left(-\infty ,0\right)[/latex]
- has a horizontal asymptote at [latex]y=0[/latex] and domain of [latex]\left(-\infty ,\infty \right)[/latex], which are unchanged from the parent function.
The function [latex]f\left(x\right)={b}^{-x}[/latex]
- reflects the parent function [latex]f\left(x\right)={b}^{x}[/latex] about the y-axis.
- has a y-intercept of [latex]\left(0,1\right)[/latex], a horizontal asymptote at [latex]y=0[/latex], a range of [latex]\left(0,\infty \right)[/latex], and a domain of [latex]\left(-\infty ,\infty \right)[/latex], which are unchanged from the parent function.
Example 9: Writing and Graphing the Reflection of an Exponential Function
Find and graph the equation for a function, [latex]g\left(x\right)[/latex], that reflects [latex]f\left(x\right)={\left(\frac{1}{4}\right)}^{x}[/latex] about the x-axis. State its domain, range, and asymptote.
Try It
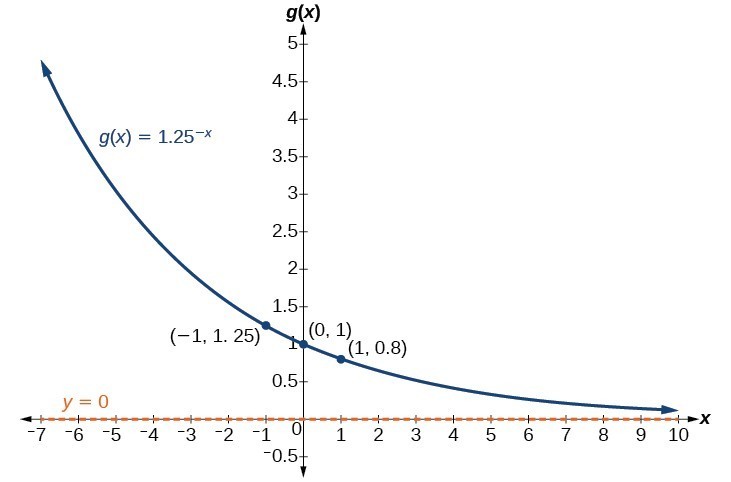
Find and graph the equation for a function, [latex]g\left(x\right)[/latex], that reflects [latex]f\left(x\right)={1.25}^{x}[/latex] about the y-axis. State its domain, range, and asymptote.
Try It
Summarizing Translations of the Exponential Function
Now that we have worked with each type of translation for the exponential function, we can summarize them to arrive at the general equation for translating exponential functions.
| Translations of the Parent Function [latex]f\left(x\right)={b}^{x}[/latex] | |
|---|---|
| Translation | Form |
Shift
|
[latex]f\left(x\right)={b}^{x+c}+d[/latex] |
Stretch and Compress
|
[latex]f\left(x\right)=a{b}^{x}[/latex] |
| Reflect about the x-axis | [latex]f\left(x\right)=-{b}^{x}[/latex] |
| Reflect about the y-axis | [latex]f\left(x\right)={b}^{-x}={\left(\frac{1}{b}\right)}^{x}[/latex] |
| General equation for all translations | [latex]f\left(x\right)=a{b}^{x+c}+d[/latex] |
A General Note: Translations of Exponential Functions
A translation of an exponential function has the form
Where the parent function, [latex]y={b}^{x}[/latex], [latex]b>1[/latex], is
- shifted horizontally c units to the left.
- stretched vertically by a factor of |a| if |a| > 0.
- compressed vertically by a factor of |a| if 0 < |a| < 1.
- shifted vertically d units.
- reflected about the x-axis when a < 0.
Note the order of the shifts, transformations, and reflections follow the order of operations.
Example 10: Writing a Function from a Description
Write the equation for the function described below. Give the horizontal asymptote, the domain, and the range.
[latex]f\left(x\right)={e}^{x}[/latex] is vertically stretched by a factor of 2, reflected across the y-axis, and then shifted up 4 units.
Try It
Write the equation for function described below. Give the horizontal asymptote, the domain, and the range.
[latex]f\left(x\right)={e}^{x}[/latex] is compressed vertically by a factor of [latex]\frac{1}{3}[/latex], reflected across the x-axis and then shifted down 2 units.
Key Equations
| General Form for the Translation of the Parent Function [latex]\text{ }f\left(x\right)={b}^{x}[/latex] | [latex]f\left(x\right)=a{b}^{x+c}+d[/latex] |
| definition of the exponential function | [latex]f\left(x\right)={b}^{x}\text{, where }b>0, b\ne 1[/latex] |
| definition of exponential growth | [latex]f\left(x\right)=a{b}^{x},\text{ where }a>0,b>0,b\ne 1[/latex] |
| compound interest formula | [latex]\begin{cases}A\left(t\right)=P{\left(1+\frac{r}{n}\right)}^{nt} ,\text{ where}\hfill \\ A\left(t\right)\text{ is the account value at time }t\hfill \\ t\text{ is the number of years}\hfill \\ P\text{ is the initial investment, often called the principal}\hfill \\ r\text{ is the annual percentage rate (APR), or nominal rate}\hfill \\ n\text{ is the number of compounding periods in one year}\hfill \end{cases}[/latex] |
| continuous compounding formula | [latex]A\left(t\right)=P{e}^{rt},\text{ where }[/latex]t is the number of unit time periods of growth, (typically in years).
e is the mathematical constant, [latex] e\approx 2.718282[/latex] |
Key Concepts
- An exponential function is defined as a function with a positive constant other than 1 raised to a variable exponent.
- A function is evaluated by solving at a specific value.
- An exponential model can be found when the growth rate and initial value are known.
- An exponential model can be found when the two data points from the model are known.
- An exponential model can be found using two data points from the graph of the model.
- An exponential model can be found using two data points from the graph and a calculator.
- The value of an account at any time t can be calculated using the compound interest formula when the principal, annual interest rate, and compounding periods are known.
- The initial investment of an account can be found using the compound interest formula when the value of the account, annual interest rate, compounding periods, and life span of the account are known.
- The number e is a mathematical constant often used as the base of real world exponential growth and decay models. Its decimal approximation is [latex]e\approx 2.718282[/latex].
- Scientific and graphing calculators have the key [latex]\left[{e}^{x}\right][/latex] or [latex]\left[\mathrm{exp}\left(x\right)\right][/latex] for calculating powers of e.
- Continuous growth or decay models are exponential models that use e as the base. Continuous growth and decay models can be found when the initial value and growth or decay rate are known.
- The graph of the function [latex]f\left(x\right)={b}^{x}[/latex] has a y-intercept at [latex]\left(0, 1\right)[/latex], domain [latex]\left(-\infty , \infty \right)[/latex], range [latex]\left(0, \infty \right)[/latex], and horizontal asymptote [latex]y=0[/latex].
- If [latex]b>1[/latex], the function is increasing. The left tail of the graph will approach the asymptote [latex]y=0[/latex], and the right tail will increase without bound.
- If 0 < b < 1, the function is decreasing. The left tail of the graph will increase without bound, and the right tail will approach the asymptote [latex]y=0[/latex].
- The equation [latex]f\left(x\right)={b}^{x}+d[/latex] represents a vertical shift of the parent function [latex]f\left(x\right)={b}^{x}[/latex].
- The equation [latex]f\left(x\right)={b}^{x+c}[/latex] represents a horizontal shift of the parent function [latex]f\left(x\right)={b}^{x}[/latex].
- Approximate solutions of the equation [latex]f\left(x\right)={b}^{x+c}+d[/latex] can be found using a graphing calculator.
- The equation [latex]f\left(x\right)=a{b}^{x}[/latex], where [latex]a>0[/latex], represents a vertical stretch if [latex]|a|>1[/latex] or compression if [latex]0<|a|<1[/latex] of the parent function [latex]f\left(x\right)={b}^{x}[/latex].
- When the parent function [latex]f\left(x\right)={b}^{x}[/latex] is multiplied by –1, the result, [latex]f\left(x\right)=-{b}^{x}[/latex], is a reflection about the x-axis. When the input is multiplied by –1, the result, [latex]f\left(x\right)={b}^{-x}[/latex], is a reflection about the y-axis.
- All translations of the exponential function can be summarized by the general equation [latex]f\left(x\right)=a{b}^{x+c}+d[/latex].
- Using the general equation [latex]f\left(x\right)=a{b}^{x+c}+d[/latex], we can write the equation of a function given its description.
Glossary
- annual percentage rate (APR)
- the yearly interest rate earned by an investment account, also called nominal rate
- compound interest
- interest earned on the total balance, not just the principal
- exponential growth
- a model that grows by a rate proportional to the amount present
- nominal rate
- the yearly interest rate earned by an investment account, also called annual percentage rate
Section 3.1 Homework Exercises
1. Explain why the values of an increasing exponential function will eventually overtake the values of an increasing linear function.
2. Given a formula for an exponential function, is it possible to determine whether the function grows or decays exponentially just by looking at the formula? Explain.
3. What role does the horizontal asymptote of an exponential function play in telling us about the end behavior of the graph?
For the following exercises, identify whether the statement represents an exponential function. Explain.
4. The average annual population increase of a pack of wolves is 25.
5. A population of bacteria decreases by a factor of [latex]\frac{1}{8}[/latex] every 24 hours.
6. The value of a coin collection has increased by 3.25% annually over the last 20 years.
7. For each training session, a personal trainer charges his clients $5 less than the previous training session.
8. The height of a projectile at time t is represented by the function [latex]h\left(t\right)=-4.9{t}^{2}+18t+40[/latex].
For the following exercises, consider this scenario: For each year t, the population of a forest of trees is represented by the function [latex]A\left(t\right)=115{\left(1.025\right)}^{t}[/latex]. In a neighboring forest, the population of the same type of tree is represented by the function [latex]B\left(t\right)=82{\left(1.029\right)}^{t}[/latex]. (Round answers to the nearest whole number.)
9. Which forest’s population is growing at a faster rate?
10. Which forest had a greater number of trees initially? By how many?
11. Assuming the population growth models continue to represent the growth of the forests, which forest will have a greater number of trees after 20 years? By how many?
12. Assuming the population growth models continue to represent the growth of the forests, which forest will have a greater number of trees after 100 years? By how many?
13. Discuss the above results from the previous four exercises. Assuming the population growth models continue to represent the growth of the forests, which forest will have the greater number of trees in the long run? Why? What are some factors that might influence the long-term validity of the exponential growth model?
For the following exercises, determine whether the equation represents exponential growth, exponential decay, or neither. Explain.
14. [latex]y=300{\left(1-t\right)}^{5}[/latex]
15. [latex]y=220{\left(1.06\right)}^{x}[/latex]
16. [latex]y=16.5{\left(1.025\right)}^{\frac{1}{x}}[/latex]
17. [latex]y=11,701{\left(0.97\right)}^{t}[/latex]
For the following exercises, find the formula for an exponential function that passes through the two points given.
18. [latex]\left(0,6\right)[/latex] and [latex]\left(3,750\right)[/latex]
19. [latex]\left(0,2000\right)[/latex] and [latex]\left(2,20\right)[/latex]
20. [latex]\left(-1,\frac{3}{2}\right)[/latex] and [latex]\left(3,24\right)[/latex]
21. [latex]\left(-2,6\right)[/latex] and [latex]\left(3,1\right)[/latex]
22. [latex]\left(3,1\right)[/latex] and [latex]\left(5,4\right)[/latex]
For the following exercises, use the compound interest formula, [latex]A\left(t\right)=P{\left(1+\frac{r}{n}\right)}^{nt}[/latex].
23. What was the initial deposit made to the account in the previous exercise?
24. How many years had the account from the previous exercise been accumulating interest?
25. An account is opened with an initial deposit of $6,500 and earns 3.6% interest compounded semi-annually. What will the account be worth in 20 years?
26. How much more would the account in the previous exercise have been worth if the interest were compounding weekly?
27. Solve the compound interest formula for the principal, P.
28. Use the formula found in the previous exercise to calculate the initial deposit of an account that is worth $14,472.74 after earning 5.5% interest compounded monthly for 5 years. (Round to the nearest dollar.)
29. How much more would the account in the previous two exercises be worth if it were earning interest for 5 more years?
30. Use properties of rational exponents to solve the compound interest formula for the interest rate, r.
31. Use the formula found in the previous exercise to calculate the interest rate for an account that was compounded semi-annually, had an initial deposit of $9,000 and was worth $13,373.53 after 10 years.
32. Use the formula found in the previous exercise to calculate the interest rate for an account that was compounded monthly, had an initial deposit of $5,500, and was worth $38,455 after 30 years.
For the following exercises, determine whether the equation represents continuous growth, continuous decay, or neither. Explain.
33. [latex]y=3742{\left(e\right)}^{0.75t}[/latex]
34. [latex]y=150{\left(e\right)}^{\frac{3.25}{t}}[/latex]
35. Suppose an investment account is opened with an initial deposit of $12,000 earning 7.2% interest compounded continuously. How much will the account be worth after 30 years?
36. How much less would the account from Exercise 35 be worth after 30 years if it were compounded monthly instead?
37. Determine the rate that represents the better deal: 7% compounded semiannually or 6.9% compounded continuously?
38. Determine the rate that represents the better deal: 9% compounded annually or 8.9% compounded continuously?
39. The graph of [latex]f\left(x\right)={3}^{x}[/latex] is reflected about the y-axis and stretched vertically by a factor of 4. What is the equation of the new function, [latex]g\left(x\right)[/latex]? State its y-intercept, domain, and range.
40. The graph of [latex]f\left(x\right)={\left(\frac{1}{2}\right)}^{-x}[/latex] is reflected about the y-axis and compressed vertically by a factor of [latex]\frac{1}{5}[/latex]. What is the equation of the new function, [latex]g\left(x\right)[/latex]? State its y-intercept, domain, and range.
41. The graph of [latex]f\left(x\right)={10}^{x}[/latex] is reflected about the x-axis and shifted upward 7 units. What is the equation of the new function, [latex]g\left(x\right)[/latex]? State its y-intercept, domain, and range.
42. The graph of [latex]f\left(x\right)={\left(1.68\right)}^{x}[/latex] is shifted right 3 units, stretched vertically by a factor of 2, reflected about the x-axis, and then shifted downward 3 units. What is the equation of the new function, [latex]g\left(x\right)[/latex]? State its y-intercept (to the nearest thousandth), domain, and range.
43. The graph of [latex]f\left(x\right)=-\frac{1}{2}{\left(\frac{1}{4}\right)}^{x - 2}+4[/latex] is shifted left 2 units, stretched vertically by a factor of 4, reflected about the x-axis, and then shifted downward 4 units. What is the equation of the new function, [latex]g\left(x\right)[/latex]? State its y-intercept, domain, and range.
For the following exercises, graph the function and its reflection about the y-axis on the same axes, and give the y-intercept.
44. [latex]f\left(x\right)=3{\left(\frac{1}{2}\right)}^{x}[/latex]
45. [latex]g\left(x\right)=-2{\left(0.25\right)}^{x}[/latex]
46. [latex]h\left(x\right)=6{\left(1.75\right)}^{-x}[/latex]
For the following exercises, graph each set of functions on the same axes.
47. [latex]f\left(x\right)=3{\left(\frac{1}{4}\right)}^{x}[/latex], [latex]g\left(x\right)=3{\left(2\right)}^{x}[/latex], and [latex]h\left(x\right)=3{\left(4\right)}^{x}[/latex]
48. [latex]f\left(x\right)=\frac{1}{4}{\left(3\right)}^{x}[/latex], [latex]g\left(x\right)=2{\left(3\right)}^{x}[/latex], and [latex]h\left(x\right)=4{\left(3\right)}^{x}[/latex]
For the following exercises, match each function with one of the graphs pictured below.

49. [latex]f\left(x\right)=2{\left(0.69\right)}^{x}[/latex]
50. [latex]f\left(x\right)=2{\left(1.28\right)}^{x}[/latex]
51. [latex]f\left(x\right)=2{\left(0.81\right)}^{x}[/latex]
52. [latex]f\left(x\right)=4{\left(1.28\right)}^{x}[/latex]
53. [latex]f\left(x\right)=2{\left(1.59\right)}^{x}[/latex]
54. [latex]f\left(x\right)=4{\left(0.69\right)}^{x}[/latex]
For the following exercises, use the graphs shown below. All have the form [latex]f\left(x\right)=a{b}^{x}[/latex].

55. Which graph has the largest value for b?
56. Which graph has the smallest value for b?
57. Which graph has the largest value for a?
58. Which graph has the smallest value for a?
For the following exercises, graph the function and its reflection about the x-axis on the same axes.
59. [latex]f\left(x\right)=\frac{1}{2}{\left(4\right)}^{x}[/latex]
60. [latex]f\left(x\right)=3{\left(0.75\right)}^{x}-1[/latex]
61. [latex]f\left(x\right)=-4{\left(2\right)}^{x}+2[/latex]
For the following exercises, graph the transformation of [latex]f\left(x\right)={2}^{x}[/latex]. Give the horizontal asymptote, the domain, and the range.
62. [latex]f\left(x\right)={2}^{-x}[/latex]
63. [latex]h\left(x\right)={2}^{x}+3[/latex]
64. [latex]f\left(x\right)={2}^{x - 2}[/latex]
For the following exercises, describe the end behavior of the graphs of the functions.
65. [latex]f\left(x\right)=-5{\left(4\right)}^{x}-1[/latex]
66. [latex]f\left(x\right)=3{\left(\frac{1}{2}\right)}^{x}-2[/latex]
67. [latex]f\left(x\right)=3{\left(4\right)}^{-x}+2[/latex]
For the following exercises, start with the graph of [latex]f\left(x\right)={4}^{x}[/latex]. Then write a function that results from the given transformation.
68. Shift f(x) 4 units upward
69. Shift f(x) 3 units downward
70. Shift f(x) 2 units left
71. Shift f(x) 5 units right
72. Reflect f(x) about the x-axis
73. Reflect f(x) about the y-axis
For the following exercises, each graph is a transformation of [latex]y={2}^{x}[/latex]. Write an equation describing the transformation.
74.

75.

76.

For the following exercises, find an exponential equation for the graph.
77.

78.

For the following exercises, evaluate the exponential functions for the indicated value of x.
79. [latex]g\left(x\right)=\frac{1}{3}{\left(7\right)}^{x - 2}[/latex] for [latex]g\left(6\right)[/latex].
80. [latex]f\left(x\right)=4{\left(2\right)}^{x - 1}-2[/latex] for [latex]f\left(5\right)[/latex].
81. [latex]h\left(x\right)=-\frac{1}{2}{\left(\frac{1}{2}\right)}^{x}+6[/latex] for [latex]h\left(-7\right)[/latex].
For the following exercises, use a graphing calculator to approximate the solutions of the equation. Round to the nearest thousandth. [latex]f\left(x\right)=a{b}^{x}+d[/latex].
82. [latex]-50=-{\left(\frac{1}{2}\right)}^{-x}[/latex]
83. [latex]116=\frac{1}{4}{\left(\frac{1}{8}\right)}^{x}[/latex]
84. [latex]12=2{\left(3\right)}^{x}+1[/latex]
85. [latex]5=3{\left(\frac{1}{2}\right)}^{x - 1}-2[/latex]
86. [latex]-30=-4{\left(2\right)}^{x+2}+2[/latex]
87. In an exponential decay function, the base of the exponent is a value between 0 and 1. Thus, for some number [latex]b>1[/latex], the exponential decay function can be written as [latex]f\left(x\right)=a\cdot {\left(\frac{1}{b}\right)}^{x}[/latex]. Use this formula, along with the fact that [latex]b={e}^{n}[/latex], to show that an exponential decay function takes the form [latex]f\left(x\right)=a{\left(e\right)}^{-nx}[/latex] for some positive number n.
88. The formula for the amount A in an investment account with a nominal interest rate r at any time t is given by [latex]A\left(t\right)=a{\left(e\right)}^{rt}[/latex], where a is the amount of principal initially deposited into an account that compounds continuously. Prove that the percentage of interest earned to principal at any time t can be calculated with the formula [latex]I\left(t\right)={e}^{rt}-1[/latex].
89. The fox population in a certain region has an annual growth rate of 9% per year. In the year 2012, there were 23,900 fox counted in the area. What is the fox population predicted to be in the year 2020?
90. An investment account with an annual interest rate of 7% was opened with an initial deposit of $4,000 Compare the values of the account after 9 years when the interest is compounded annually, quarterly, monthly, and continuously.
91. Alyssa opened a retirement account with 7.25% APR in the year 2000. Her initial deposit was $13,500. How much will the account be worth in 2025 if interest compounds monthly? How much more would she make if interest compounded continuously?
92. Recall that an exponential function is any equation written in the form [latex]f\left(x\right)=a\cdot {b}^{x}[/latex] such that a and b are positive numbers and [latex]b\ne 1[/latex]. Any positive number b can be written as [latex] b={e}^{n}[/latex] for some value of n. Use this fact to rewrite the formula for an exponential function that uses the number e as a base.
93. Explore and discuss the graphs of [latex]F\left(x\right)={\left(b\right)}^{x}[/latex] and [latex]G\left(x\right)={\left(\frac{1}{b}\right)}^{x}[/latex]. Then make a conjecture about the relationship between the graphs of the functions [latex]{b}^{x}[/latex] and [latex]{\left(\frac{1}{b}\right)}^{x}[/latex] for any real number [latex]b>0[/latex].
94. Prove the conjecture made in the previous exercise.
95. Explore and discuss the graphs of [latex]f\left(x\right)={4}^{x}[/latex], [latex]g\left(x\right)={4}^{x - 2}[/latex], and [latex]h\left(x\right)=\left(\frac{1}{16}\right){4}^{x}[/latex]. Then make a conjecture about the relationship between the graphs of the functions [latex]{b}^{x}[/latex] and [latex]\left(\frac{1}{{b}^{n}}\right){b}^{x}[/latex] for any real number n and real number [latex]b>0[/latex].
96. Prove the conjecture made in the previous exercise.
- Todar, PhD, Kenneth. Todar's Online Textbook of Bacteriology. http://textbookofbacteriology.net/growth_3.html. ↵
- http://www.worldometers.info/world-population/. Accessed February 24, 2014. ↵