Section 4.4: Reference Angles

Reference Angles

An angle’s reference angle is the measure of the smallest, positive, acute angle $t$ formed by the terminal side of the angle $t$ and the horizontal axis. Thus positive reference angles have terminal sides that lie in the first quadrant and can be used as models for angles in other quadrants. See Figure 1 for examples of reference angles for angles in different quadrants.

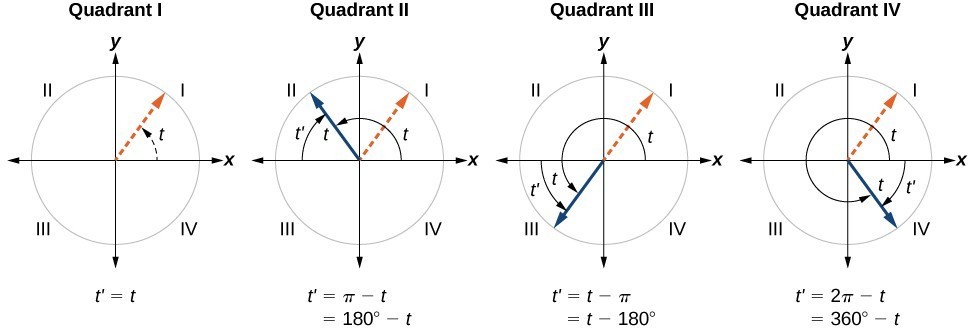
Four side by side graphs. First graph shows an angle of t in quadrant 1 in it's normal position. Second graph shows an angle of t in quadrant 2 due to a rotation of pi minus t. Third graph shows an angle of t in quadrant 3 due to a rotation of t minus pi. Fourth graph shows an angle of t in quadrant 4 due to a rotation of two pi minus t.

Figure 1

A GENERAL NOTE: REFERENCE ANGLES

An angle’s reference angle is the size of the smallest acute angle, ${t}^{\prime }$ , formed by the terminal side of the angle $t$ and the horizontal axis.

How To: Given an angle between $0$ and $2\pi$ , find its reference angle.

An angle in the first quadrant is its own reference angle.
For an angle in the second or third quadrant, the reference angle is $|\pi -t|$ or $|180^\circ \mathrm{-t}|$ .
For an angle in the fourth quadrant, the reference angle is $2\pi -t$ or $360^\circ \mathrm{-t}$ .
If an angle is less than $0$ or greater than $2\pi$ , add or subtract $2\pi$ as many times as needed to find an equivalent angle between $0$ and $2\pi$ .

Example 1: Finding a Reference Angle

Find the reference angle of $225^\circ$ as shown in Figure 2.

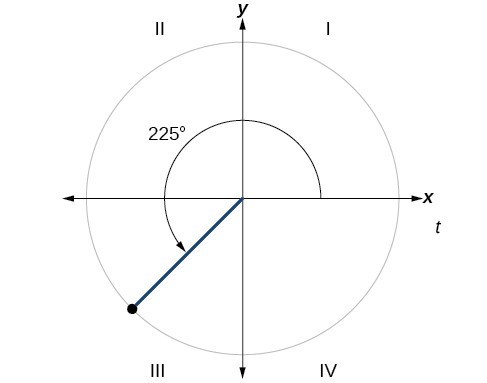
Graph of circle with 225 degree angle inscribed.

Figure 2

Show Solution

Because $225^\circ$ is in the third quadrant, the reference angle is

$|\left(180^\circ -225^\circ \right)|=|-45^\circ |=45^\circ$

Try It

Find the reference angle of $\frac{5\pi }{3}$ .

Show Solution

$\frac{\pi }{3}$

Using Reference Angles

Reference angles make it possible to evaluate trigonometric functions for angles outside the first quadrant. They can also be used to find $\left(x,y\right)$ coordinates for those angles. We will use the reference angle of the angle of rotation combined with the quadrant in which the terminal side of the angle lies. We can find the exact trig value of any angle in any quadrant if we apply the trig function to the reference angle. The sign depends on the quadrant of the original angle.

The trigonometric function values for the original angle will be the same as those for the reference angle, except for the positive or negative sign, which is determined by x– and y-values in the original quadrant. Figure 3 shows which functions are positive in which quadrant.

To help us remember which of the six trigonometric functions are positive in each quadrant, we can use the mnemonic phrase “All Students Take Calculus” Each of the four words in the phrase corresponds to one of the four quadrants, starting with quadrant I and rotating counterclockwise. In quadrant I, which is “A,” all of the six trigonometric functions are positive. In quadrant II, “Students,” only sine and its reciprocal function, cosecant, are positive. In quadrant III, “Take,” only tangent and its reciprocal function, cotangent, are positive. Finally, in quadrant IV, “Calculus” only cosine and its reciprocal function, secant, are positive.

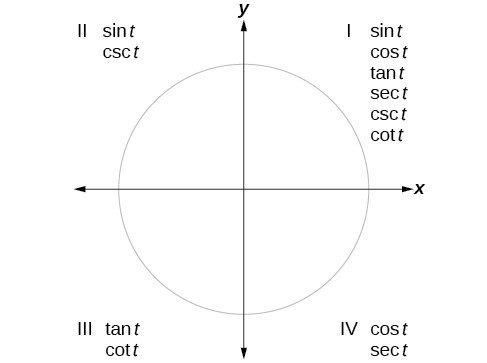
Graph of circle with each quadrant labeled. Under quadrant 1, labels fro sin t, cos t, tan t, sec t, csc t, and cot t. Under quadrant 2, labels for sin t and csc t. Under quadrant 3, labels for tan t and cot t. Under quadrant 4, labels for cos t, sec t.

Figure 3

How To: Find the trigonometric value for any angle

Measure the angle between the terminal side of the given angle and the horizontal axis. This is the reference angle.
Apply the trig function to the reference angle.
Apply the appropriate sign using the table above.

Example 2: Using Reference Angles to Find Sine and Cosine

Using a reference angle, find the exact value of $\cos \left(150^\circ \right)$ and $\text{sin}\left(150^\circ \right)$ .
Using the reference angle, find $\cos \frac{5\pi }{4}$ and $\sin \frac{5\pi }{4}$ .

Show Solution

150° is located in the second quadrant. The angle it makes with the x-axis is 180° − 150° = 30°, so the reference angle is 30°. This tells us that 150° has the same sine and cosine values as 30°, except for the sign. We know that
$\cos \left(30^\circ \right)=\frac{\sqrt{3}}{2}\text{ and }\sin \left(30^\circ \right)=\frac{1}{2}$ .

Since 150° is in the second quadrant, the x-coordinate of the point on the circle is negative, so the cosine value is negative. The y-coordinate is positive, so the sine value is positive.

$\cos \left(150^\circ \right)=-\frac{\sqrt{3}}{2}\text{ and }\sin \left(150^\circ \right)=\frac{1}{2}$
$\frac{5\pi }{4}$ is in the third quadrant. Its reference angle is $\frac{5\pi }{4}-\pi =\frac{\pi }{4}$ . The cosine and sine of $\frac{\pi }{4}$ are both $\frac{\sqrt{2}}{2}$ . In the third quadrant, both $x$ and $y$ are negative, so:
$\cos \frac{5\pi }{4}=-\frac{\sqrt{2}}{2}\text{ and }\sin \frac{5\pi }{4}=-\frac{\sqrt{2}}{2}$

Example 3: Using Reference Angles to Find Tangent and Cotangent

Using a reference angle, find the exact value of $\tan \left(240^\circ \right)$
Using the reference angle, find $\cot \frac{7\pi }{4}$

Show Solution

240° is located in the third quadrant. The angle it makes with the x-axis is 240° − 180° = 60°, so the reference angle is 60°. This tells us that 240° has the same tangent values as 60°, except for the sign. We know that
$\tan \left(60^\circ \right)=\sqrt{3}$ .

Since 240° is in the second quadrant, the x-coordinate of the point on the circle is positive, so the tangent value is positive.

$\tan \left(240^\circ \right)=\sqrt{3}$
$\frac{7\pi }{4}$ is in the fourth quadrant. Its reference angle is $2\pi-\frac{7\pi }{4} =\frac{\pi }{4}$ . The cotangent of $\frac{\pi }{4}$ is $\frac{2}{\sqrt{2}}=\sqrt{2}$ . In the fourth quadrant, cotangent is negative, so
$\cot \frac{7\pi }{4}=-\sqrt{2}$

Example 4: Using Reference Angles to Find Secant and Cosecant

Using a reference angle, find the exact value of $\sec \left(210^\circ \right)$ and $\csc\left(210^\circ \right)$ .
Using the reference angle, find $\sec \frac{3\pi }{4}$ and $\csc \frac{3\pi }{4}$ .

Show Solution

150° is located in the second quadrant. The angle it makes with the x-axis is 210° − 180° = 30°, so the reference angle is 30°. This tells us that 210° has the same sine and cosine values as 30°, except for the sign. We know that
$\sec \left(30^\circ \right)=\frac{2}{\sqrt{3}}=\frac{2\sqrt{3}}{3}\text{ and }\csc \left(30^\circ \right)=2$ .

Since 210° is in the second quadrant, the x-coordinate of the point on the circle is negative, so the sec value is negative. The y-coordinate is negative, so the sine value is also negative.

$\sec \left(210^\circ \right)=-\frac{2\sqrt{3}}{3}\text{ and }\csc \left(210^\circ \right)=-2$
$\frac{3\pi }{4}$ is in the second quadrant. Its reference angle is $\pi-\frac{3\pi }{4} =\frac{\pi }{4}$ . The secant and cosecant of $\frac{\pi }{4}$ are both $\frac{2}{\sqrt{2}}=\sqrt{2}$ . In the second quadrant, $x$ is negative and $y$ is positive, so:
$\sec \frac{3\pi }{4}=-\sqrt{2}\text{ and }\csc \frac{3\pi }{4}=\sqrt{2}$

Try It

a. Use the reference angle of $315^\circ$ to find $\cos \left(315^\circ \right)$ and $\tan \left(315^\circ \right)$ .

b. Use the reference angle of $\frac{2\pi }{3}$ to find $\sec \left(\frac{2\pi }{3}\right)$ and $\cot \left(\frac{2\pi }{3}\right)$ .

Show Solution

a. $\text{cos}\left(315^\circ \right)=\frac{\sqrt{2}}{2},\text{tan}\left(315^\circ \right)=-1$
b. $\cos \left(\frac{2\pi }{3}\right)=-\frac{1}{2},\cot \left(\frac{2\pi }{3}\right)=-\frac{\sqrt{3}}{3}$

Try It

Example 5: Using Reference Angles to Find Trigonometric Functions

Use reference angles to find all six trigonometric functions of $-\frac{5\pi }{6}$ .

Show Solution

In order to find a reference angle for a negative angle, add $2\pi$ until the angle becomes positive: $-\frac{5\pi}{6}+2\pi=\frac{7\pi}{6}$ . This angle is in the third quadrant, so the reference angle is: $\frac{7\pi}{6}-\pi=\frac{\pi}{6}$ . Since $\frac{7\pi }{6}$ is in the third quadrant, where both $x$ and $y$ are negative, sine, cosecant, cosine, and secant will be negative, while tangent and cotangent will be positive.

$\begin{gathered}\cos \left(-\frac{5\pi }{6}\right)=-\frac{\sqrt{3}}{2} \\ \sin \left(-\frac{5\pi }{6}\right)=-\frac{1}{2} \\ \tan\left(-\frac{5\pi }{6}\right)=\frac{\sqrt{3}}{3} \\ \sec\left(-\frac{5\pi }{6}\right)=-\frac{2\sqrt{3}}{3}\\ \csc\left(-\frac{5\pi }{6}\right)=-2\\ \cot \left(-\frac{5\pi }{6}\right)=\sqrt{3} \end{gathered}$

Try It

Use reference angles to find all six trigonometric functions of $-\frac{7\pi }{4}$ .

Show Solution

$\sin \left(-\frac{7\pi }{4}\right)=\frac{\sqrt{2}}{2},\cos \left(-\frac{7\pi }{4}\right)=\frac{\sqrt{2}}{2},\tan \left(-\frac{7\pi }{4}\right)=1$ ,
$\sec \left(-\frac{7\pi }{4}\right)=\sqrt{2},\csc \left(-\frac{7\pi }{4}\right)=\sqrt{2},\cot \left(-\frac{7\pi }{4}\right)=1$

Example 6: Using Reference Angles to Find Trigonometric Functions

Use reference angles to find all six trigonometric functions of $-585^\circ$ .

Show Solution

We need to add $360^\circ$ until the angle becomes positive. In this case, we needed to add it twice: $-585^\circ+360^\circ+360^\circ=135^\circ$ . This angle is in the second quadrant, so the reference angle is: $180^\circ-135=45^\circ$ . Since $45^\circ$ is in the second quadrant, where $x$ is negative and $y$ is positive, cosine, secant, tangent, and cotangent will be negative, while sine and cosecant will be positive.

$\begin{gathered}\cos \left(-585^\circ\right)=-\frac{\sqrt{2}}{2} \\ \sec \left(-585^\circ\right)=-\sqrt{2} \\ \tan\left(-585^\circ\right)=-1 \\ \cot\left(-585^\circ\right)=-1\\ \sin\left(-585^\circ\right)=\frac{\sqrt{2}}{2}\\ \csc \left(-585^\circ\right)=\sqrt{2} \end{gathered}$

Try It

Example 7: Using the Unit Circle to Find Coordinates

Find the coordinates of the point on the unit circle at an angle of $\frac{7\pi }{6}$ .

Show Solution

We know that the angle $\frac{7\pi }{6}$ is in the third quadrant.

First, let’s find the reference angle by measuring the angle to the x-axis. To find the reference angle of an angle whose terminal side is in quadrant III, we find the difference of the angle and $\pi$ .

$\frac{7\pi }{6}-\pi =\frac{\pi }{6}$

Next, we find the cosine and sine of the reference angle:

$\begin{gathered}\cos \left(\frac{\pi }{6}\right)=\frac{\sqrt{3}}{2} \\ \sin \left(\frac{\pi }{6}\right)=\frac{1}{2}\end{gathered}$

We must determine the appropriate signs for x and y in the given quadrant. Because our original angle is in the third quadrant, where both $x$ and $y$ are negative, both cosine and sine are negative.

$\begin{gathered}\cos \left(\frac{7\pi }{6}\right)=-\frac{\sqrt{3}}{2} \\ \sin \left(\frac{7\pi }{6}\right)=-\frac{1}{2} \end{gathered}$

Now we can calculate the $\left(x,y\right)$ coordinates using the identities $x=\cos \theta$ and $y=\sin \theta$ .

The coordinates of the point are $\left(-\frac{\sqrt{3}}{2},-\frac{1}{2}\right)$ on the unit circle.

Try It

Find the coordinates of the point on the unit circle at an angle of $\frac{5\pi }{3}$ .

Show Solution

$\left(\frac{1}{2},-\frac{\sqrt{3}}{2}\right)$

Example 8: Finding the Exact Value Involving Tangent

Given that $\tan \theta =−\frac{3}{4}$ and $\theta$ is in quadrant II, find the following:

$\sin \left(\theta \right)$
$\csc \left(\theta \right)$
$\cos \left(\theta \right)$
$\sec \left(\theta \right)$
$\cot \left(\theta \right)$

Show Solution

If we draw a triangle to reflect the information given, we can find the values needed to solve the problems on the image. We are given $\tan \theta =-\frac{3}{4}$ , such that $\theta$ is in quadrant II. The tangent of an angle is equal to the opposite side over the adjacent side, and because $\theta$ is in the second quadrant, the adjacent side is on the x-axis and is negative. Use the Pythagorean Theorem to find the length of the hypotenuse:

$\begin{align}{\left(-4\right)}^{2}+{\left(3\right)}^{2}&={c}^{2}\\ 16+9&={c}^{2}\\ 25&={c}^{2}\\ c&=5\end{align}$

Now we can draw a triangle similar to the one shown in Figure 4.

Diagram of a triangle in the x,y-plane. The vertices are at the origin, (-4,0), and (-4,3). The angle at the origin is theta. The angle formed by the side (-4,3) to (-4,0) forms a right angle with the x axis. The hypotenuse across from the right angle is length 5.

Figure 4

Now that we know all the sides of the triangle, we can use right triangle trigonometry definitions to find the answers:

$\begin{gathered}\sin \left(\theta\right)=\frac{3}{5} \\ \csc \left(\theta\right)=\frac{5}{3} \\ \cos\left(\theta\right)=-\frac{4}{5} \\ \sec\left(\theta\right)=-\frac{5}{4}\\ \cot\left(\theta\right)=−\frac{4}{3} \end{gathered}$

Try It

Given that $\tan \theta =\frac{5}{12}$ and $\theta$ is in quadrant III, find the following:

$\sin \left(\theta \right)$
$\csc \left(\theta \right)$
$\cos \left(\theta \right)$
$\sec \left(\theta \right)$
$\cot \left(\theta \right)$

Show Solution

$\sin \left(\theta\right)=-\frac{5}{13},\csc \left(\theta\right)=-\frac{13}{5},\cot \left(\theta\right)=\frac{12}{5}$ ,
$\cos \left(\theta\right)=-\frac{12}{13},\sec \left(\theta\right)=-\frac{13}{12}$

Key Equations

Cosine	$\cos t=x$
Sine	$\sin t=y$
Pythagorean Identity	${\cos }^{2}t+{\sin }^{2}t=1$

Key Concepts

The sine and cosine of an angle have the same absolute value as the sine and cosine of its reference angle.
The signs of the sine and cosine are determined from the x– and y-values in the quadrant of the original angle.
An angle’s reference angle is the size angle, $t$ , formed by the terminal side of the angle $t$ and the horizontal axis.
Reference angles can be used to find the sine and cosine of the original angle.
Reference angles can also be used to find the coordinates of a point on a circle.

Section 4.4 Homework Exercises

1. Discuss the difference between a coterminal angle and a reference angle.

2. Explain how the cosine of an angle in the second quadrant differs from the cosine of its reference angle in the unit circle.

3. Explain how the sine of an angle in the second quadrant differs from the sine of its reference angle in the unit circle.

4. What is the purpose of a reference angle?

For the following exercises, state the reference angle for the given angle.

5. $240^\circ$

6. $-170^\circ$

7. $460^\circ$

8. $-675^\circ$

9. $135^\circ$

10. $\frac{5\pi }{4}$

11. $\frac{2\pi }{3}$

12. $\frac{17\pi }{6}$

13. $-\frac{17\pi }{3}$

14. $-\frac{7\pi }{4}$

15. $-\frac{\pi }{8}$

For the following exercises, find the reference angle, the quadrant of the terminal side, and the sine, cosine of each angle.

16. $225^\circ$

17. $300^\circ$

18. $315^\circ$

19. $135^\circ$

20. $570^\circ$

21. $480^\circ$

22. $-120^\circ$

23. $-210^\circ$

24. $\frac{5\pi }{4}$

25. $\frac{7\pi }{6}$

26. $\frac{5\pi }{3}$

27. $\frac{3\pi }{4}$

28. $\frac{4\pi }{3}$

29. $\frac{2\pi }{3}$

30. $\frac{-19\pi }{6}$

31. $\frac{-9\pi }{4}$

For the following exercises, find the reference angle, the quadrant of the terminal side, and the exact value of the trigonometric function.

32. $\tan \frac{5\pi }{6}$

33. $\sec \frac{7\pi }{6}$

34. $\csc \frac{11\pi }{6}$

35. $\cot \frac{13\pi }{6}$

36. $\tan \frac{15\pi }{4}$

37. $\sec \frac{3\pi }{4}$

38. $\csc \frac{5\pi }{4}$

39. $\cot \frac{11\pi }{4}$

40. $\tan \left(-\frac{4\pi }{3}\right)$

41. $\sec \left(-\frac{2\pi }{3}\right)$

42. $\csc \left(-\frac{10\pi }{3}\right)$

43. $\cot \left(-\frac{7\pi }{3}\right)$

44. $\tan 225^\circ$

45. $\sec 300^\circ$

46. $\csc 510^\circ$

47. $\cot 600^\circ$

48. $\tan \left(-30^\circ\right)$

49. $\sec \left(-210^\circ\right)$

50. $\csc \left(-510^\circ\right)$

51. $\cot \left(-405^\circ\right)$

In the following exercises, use a right triangle to find the exact value.

52. If $\text{sin}t=\frac{3}{4}$ , and $t$ is in quadrant II, find $\cos t,\sec t,\csc t,\tan t,\cot t$ .

53. If $\text{cos}t=-\frac{1}{3}$ , and $t$ is in quadrant III, find $\sin t,\sec t,\csc t,\tan t,\cot t$ .

54. If $\tan t=\frac{12}{5}$ , and $0\le t<\frac{\pi }{2}$ , find $\sin t,\cos t,\sec t,\csc t$ , and $\cot t$ . 55. If $\sin t=\frac{\sqrt{3}}{2}$ and $\cos t=\frac{1}{2}$ , find $\sec t,\csc t,\tan t$ , and $\cot t$ . For the following exercises, find the exact value using reference angles. 56. $\sin\left(\frac{11\pi}{3}\right)\cos\left(\frac{-5\pi}{6}\right)$ 57. $\sin\left(\frac{3\pi}{4}\right)\cos\left(\frac{5\pi}{3}\right)$ 58. $\sin\left(\frac{-4\pi}{3}\right)\cos\left(\frac{\pi}{2}\right)$ 59. $\sin\left(\frac{-9\pi}{4}\right)\cos\left(\frac{-\pi}{6}\right)$ 60. $\sin\left(\frac{\pi}{6}\right)\cos\left(\frac{-\pi}{3}\right)$ 61. $\sin\left(\frac{7\pi}{4}\right)\cos\left(\frac{-2\pi}{3}\right)$ 62. $\cos\left(\frac{5\pi}{6}\right)\cos\left(\frac{2\pi}{3}\right)$ 63. $\cos\left(\frac{-\pi}{3}\right)\cos\left(\frac{\pi}{4}\right)$ 64. $\sin\left(\frac{-5\pi}{4}\right)\sin\left(\frac{11\pi}{6}\right)$ 65. $\sin\left(\pi\right)\sin\left(\frac{\pi}{6}\right)$

Chapter 4: Trigonometric Functions