To define our trigonometric functions, we begin by drawing a unit circle, a circle centered at the origin with radius 1, as shown in Figure 2. The angle (in radians) that $t$ intercepts forms an arc of length $s$. Using the formula $s=rt$, and knowing that $r=1$, we see that for a unit circle, $s=t$.

Recall that the x- and y-axes divide the coordinate plane into four quarters called quadrants. We label these quadrants to mimic the direction a positive angle would sweep. The four quadrants are labeled I, II, III, and IV.

For any angle $t$, we can label the intersection of the terminal side and the unit circle as by its coordinates, $\left(x,y\right)$. The coordinates $x$ and $y$ will be the outputs of the trigonometric functions $f\left(t\right)=\cos t$ and $f\left(t\right)=\sin t$, respectively. This means $x=\cos t$ and $y=\sin t$.

Figure 2. Unit circle where the central angle is $t$ radians

Defining Sine and Cosine Functions

Now that we have our unit circle labeled, we can learn how the $\left(x,y\right)$ coordinates relate to the arc length and angle. The sine function relates a real number $t$ to the y-coordinate of the point where the corresponding angle intercepts the unit circle. More precisely, the sine of an angle $t$ equals the y-value of the endpoint on the unit circle of an arc of length $t$. In Figure 2, the sine is equal to $y$. Like all functions, the sine function has an input and an output. Its input is the measure of the angle; its output is the y-coordinate of the corresponding point on the unit circle.

The cosine function of an angle $t$ equals the x-value of the endpoint on the unit circle of an arc of length $t$. In Figure 3, the cosine is equal to $x$.

Figure 3

Because it is understood that sine and cosine are functions, we do not always need to write them with parentheses: $\sin t$ is the same as $\sin \left(t\right)$ and $\cos t$ is the same as $\cos \left(t\right)$. Likewise, ${\cos }^{2}t$ is a commonly used shorthand notation for ${\left(\cos \left(t\right)\right)}^{2}$. Be aware that many calculators and computers do not recognize the shorthand notation. When in doubt, use the extra parentheses when entering calculations into a calculator or computer.

Example 1: Finding Function Values for Sine and Cosine

Point $P$ is a point on the unit circle corresponding to an angle of $t$, as shown in Figure 4. Find $\cos \left(t\right)$ and $\text{sin}\left(t\right)$.

Figure 4

Show Solution

We know that $\cos t$ is the x-coordinate of the corresponding point on the unit circle and $\sin t$ is the y-coordinate of the corresponding point on the unit circle. So:

$\begin{align} x&=\cos t=\frac{1}{2} \\ y&=\sin t=\frac{\sqrt{3}}{2} \end{align}$

Try It

A certain angle $t$ corresponds to a point on the unit circle at $\left(-\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}\right)$ as shown in Figure 5. Find $\cos t$ and $\sin t$.

Figure 5

Show Solution

$\cos \left(t\right)=-\frac{\sqrt{2}}{2},\sin \left(t\right)=\frac{\sqrt{2}}{2}$

Finding Sines and Cosines of Angles on an Axis

For quadrantral angles, the corresponding point on the unit circle falls on the x- or y-axis. In that case, we can easily calculate cosine and sine from the values of $x$ and $y$.

Example 2: Calculating Sines and Cosines along an Axis

Find $\cos \left(90^\circ \right)$ and $\text{sin}\left(90^\circ \right)$.

Show Solution

Moving $90^\circ$ counterclockwise around the unit circle from the positive x-axis brings us to the top of the circle, where the $\left(x,y\right)$ coordinates are (0, 1), as shown in Figure 6.

Figure 6

 

Using our definitions of cosine and sine,

$\begin{align}x&=\cos t=\cos \left(90^\circ \right)=0\\ y&=\sin t=\sin \left(90^\circ \right)=1\end{align}$

The cosine of 90° is 0; the sine of 90° is 1.

The Pythagorean Identity

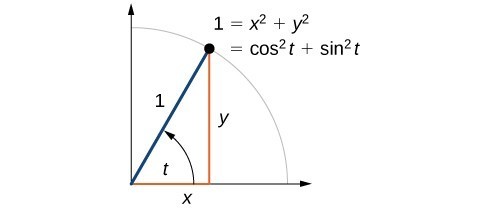
Figure 7

Now that we can define sine and cosine, we will learn how they relate to each other and the unit circle. Recall that the equation for the unit circle is ${x}^{2}+{y}^{2}=1$. Because $x=\cos t$ and $y=\sin t$, we can substitute for $x$ and $y$ to get ${\cos }^{2}t+{\sin }^{2}t=1$. This equation, ${\cos }^{2}t+{\sin }^{2}t=1$, is known as the Pythagorean Identity.

We can use the Pythagorean Identity to find the cosine of an angle if we know the sine, or vice versa. However, because the equation yields two solutions, we need additional knowledge of the angle to choose the solution with the correct sign. If we know the quadrant where the angle is, we can easily choose the correct solution.

Example 3: Finding a Cosine from a Sine or a Sine from a Cosine

If $\sin \left(t\right)=\frac{3}{7}$ and $t$ is in the second quadrant, find $\cos \left(t\right)$.

Show Solution

If we drop a vertical line from the point on the unit circle corresponding to $t$, we create a right triangle, from which we can see that the Pythagorean Identity is simply one case of the Pythagorean Theorem. 

Figure 8

 

Substituting the known value for sine into the Pythagorean Identity,

$\begin{gathered}{\cos }^{2}\left(t\right)+{\sin }^{2}\left(t\right)=1 \\ {\cos }^{2}\left(t\right)+\frac{9}{49}=1 \\ {\cos }^{2}\left(t\right)=\frac{40}{49} \\ \text{cos}\left(t\right)=\pm \sqrt{\frac{40}{49}}=\pm \frac{\sqrt{40}}{7}=\pm \frac{2\sqrt{10}}{7} \end{gathered}$

Because the angle is in the second quadrant, we know the x-value is a negative real number, so the cosine is also negative. So
$\text{cos}\left(t\right)=-\frac{2\sqrt{10}}{7}\\$

Finding Sines and Cosines of Special Angles

We have already learned some properties of the special angles, such as the conversion from radians to degrees. We can also calculate sines and cosines of the special angles using the Pythagorean Identity and our knowledge of triangles.

Finding Sines and Cosines of 45° Angles

First, we will look at angles of $45^\circ$ or $\frac{\pi }{4}$, as shown in Figure 9. A $45^\circ -45^\circ -90^\circ$ triangle is an isosceles triangle, so the x- and y-coordinates of the corresponding point on the circle are the same. Because the x- and y-values are the same, the sine and cosine values will also be equal.

Figure 9

At $t=\frac{\pi }{4}$ , which is 45 degrees, the radius of the unit circle bisects the first quadrantal angle. This means the radius lies along the line $y=x$. A unit circle has a radius equal to 1. So, the right triangle formed below the line $y=x$ has sides $x$ and $y\text{ }\left(y=x\right)$, and a radius = 1.

Figure 10

From the Pythagorean Theorem we get

Substituting $y=x$, we get

Combining like terms we get

And solving for $x$, we get

In quadrant I, $x=\frac{1}{\sqrt{2}}$.

At $t=\frac{\pi }{4}$ or 45 degrees,

If we then rationalize the denominators, we get

Therefore, the $\left(x,y\right)$ coordinates of a point on a circle of radius $1$ at an angle of $45^\circ$ are $\left(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}\right)$.

Finding Sines and Cosines of 30° and 60° Angles

Next, we will find the cosine and sine at an angle of $30^\circ$, or $\frac{\pi }{6}$ . First, we will draw a triangle inside a circle with one side at an angle of $30^\circ$, and another at an angle of $-30^\circ$, as shown in Figure 11. If the resulting two right triangles are combined into one large triangle, notice that all three angles of this larger triangle will be $60^\circ$, as shown in Figure 12.

Figure 11

Figure 12

Because all the angles are equal, the sides are also equal. The vertical line has length $2y$, and since the sides are all equal, we can also conclude that $r=2y$ or $y=\frac{1}{2}r$. Since $\sin t=y$ ,

And since $r=1$ in our unit circle,

Using the Pythagorean Identity, we can find the cosine value.

The $\left(x,y\right)$ coordinates for the point on a circle of radius $1$ at an angle of $30^\circ$ are $\left(\frac{\sqrt{3}}{2},\frac{1}{2}\right)$. At $t=\frac{\pi }{3}$ (60°), the radius of the unit circle, 1, serves as the hypotenuse of a 30-60-90 degree right triangle, $BAD$, as shown in Figure 13 below. Angle $A$ has measure $60^\circ$. At point $B$, we draw an angle $ABC$ with measure of $60^\circ$. We know the angles in a triangle sum to $180^\circ$, so the measure of angle $C$ is also $60^\circ$. Now we have an equilateral triangle. Because each side of the equilateral triangle $ABC$ is the same length, and we know one side is the radius of the unit circle, all sides must be of length 1.

Figure 13

The measure of angle $ABD$ is 30°. So, if double, angle $ABC$ is 60°. $BD$ is the perpendicular bisector of $AC$, so it cuts $AC$ in half. This means that $AD$ is $\frac{1}{2}$ the radius, or $\frac{1}{2}$. Notice that $AD$ is the x-coordinate of point $B$, which is at the intersection of the 60° angle and the unit circle. This gives us a triangle $BAD$ with hypotenuse of 1 and side $x$ of length $\frac{1}{2}$.

From the Pythagorean Theorem, we get

Substituting $x=\frac{1}{2}$, we get

Solving for $y$, we get

Since $t=\frac{\pi }{3}$ has the terminal side in quadrant I where the y-coordinate is positive, we choose [latex]y=\frac{\sqrt{3}}{2}\[/latex], the positive value.

At $t=\frac{\pi }{3}$ (60°), the $\left(x,y\right)$ coordinates for the point on a circle of radius $1$ at an angle of $60^\circ$ are [latex]\left(\frac{1}{2},\frac{\sqrt{3}}{2}\right)\[/latex], so we can find the sine and cosine.

We have now found the cosine and sine values for all of the most commonly encountered angles in the first quadrant of the unit circle. The table below summarizes these values.

Figure 14 shows the common angles in the first quadrant of the unit circle.

Figure 14

Using a Calculator to Find Sine and Cosine

To find the cosine and sine of angles other than the special angles, we turn to a computer or calculator. Be aware: Most calculators can be set into “degree” or “radian” mode, which tells the calculator the units for the input value. When we evaluate $\cos \left(30\right)$ on our calculator, it will evaluate it as the cosine of 30 degrees if the calculator is in degree mode, or the cosine of 30 radians if the calculator is in radian mode.

Identifying the Domain and Range of Sine and Cosine Functions

Now that we can find the sine and cosine of an angle, we need to discuss their domains and ranges. What are the domains of the sine and cosine functions? That is, what are the smallest and largest numbers that can be inputs of the functions? Because angles smaller than 0 and angles larger than $2\pi$ can still be graphed on the unit circle and have real values of $x,y$, and $r$, there is no lower or upper limit to the angles that can be inputs to the sine and cosine functions. The input to the sine and cosine functions is the rotation from the positive x-axis, and that may be any real number.

What are the ranges of the sine and cosine functions? What are the least and greatest possible values for their output? We can see the answers by examining the unit circle, as shown in Figure 15. The bounds of the x-coordinate are $\left[-1,1\right]$. The bounds of the y-coordinate are also $\left[-1,1\right]$. Therefore, the range of both the sine and cosine functions is $\left[-1,1\right]$.

Figure 15

We have discussed finding the sine and cosine for angles in the first quadrant, but what if our angle is in another quadrant? For any given angle in the first quadrant, there is an angle in the second quadrant with the same sine value. Because the sine value is the y-coordinate on the unit circle, the other angle with the same sine will share the same y-value, but have the opposite x-value. Therefore, its cosine value will be the opposite of the first angle’s cosine value.

Likewise, there will be an angle in the fourth quadrant with the same cosine as the original angle. The angle with the same cosine will share the same x-value but will have the opposite y-value. Therefore, its sine value will be the opposite of the original angle’s sine value.

As shown in Figure 16, angle $\alpha$ has the same sine value as angle $t$; the cosine values are opposites. Angle $\beta$ has the same cosine value as angle $t$; the sine values are opposites.

$\begin{array}{ccc}\sin \left(t\right)=\sin \left(\alpha \right)\hfill & \text{and}\hfill & \cos \left(t\right)=-\cos \left(\alpha \right)\hfill \\ \sin \left(t\right)=-\sin \left(\beta \right)\hfill & \text{and}\hfill & \cos \left(t\right)=\cos \left(\beta \right)\hfill \end{array}$

Figure 16

Find exact values of the trigonometric functions secant, cosecant, tangent, and cotangent

To define the remaining functions, we will once again draw a unit circle with a point $\left(x,y\right)$ corresponding to an angle of $t$, as shown in Figure 1. As with the sine and cosine, we can use the $\left(x,y\right)$ coordinates to find the other functions.

Figure 1

The first function we will define is the tangent. The tangent of an angle is the ratio of the y-value to the x-value of the corresponding point on the unit circle. In Figure 1, the tangent of angle $t$ is equal to $\frac{y}{x},x\ne 0$. Because the y-value is equal to the sine of $t$, and the x-value is equal to the cosine of $t$, the tangent of angle $t$ can also be defined as $\frac{\sin t}{\cos t},\cos t\ne 0$. The tangent function is abbreviated as $\tan$. The remaining three functions can all be expressed as reciprocals of functions we have already defined.

• The secant function is the reciprocal of the cosine function. In Figure 1, the secant of angle $t$ is equal to $\frac{1}{\cos t}=\frac{1}{x},x\ne 0$. The secant function is abbreviated as $\sec$.
• The cotangent function is the reciprocal of the tangent function. In Figure 1, the cotangent of angle $t$ is equal to $\frac{\cos t}{\sin t}=\frac{x}{y},y\ne 0$. The cotangent function is abbreviated as $\cot$.
• The cosecant function is the reciprocal of the sine function. In Figure 1, the cosecant of angle $t$ is equal to $\frac{1}{\sin t}=\frac{1}{y},y\ne 0$. The cosecant function is abbreviated as $\csc$.

Example 5: Finding Trigonometric Functions from a Point on the Unit Circle

The point $\left(-\frac{\sqrt{3}}{2},\frac{1}{2}\right)$ is on the unit circle, as shown in Figure 2. Find $\sin t,\cos t,\tan t,\sec t,\csc t$, and $\cot t$.

Figure 2

Show Solution

Because we know the $\left(x,y\right)$ coordinates of the point on the unit circle indicated by angle $t$, we can use those coordinates to find the six functions:

$\begin{gathered}\sin t=y=\frac{1}{2}\\ \cos t=x=-\frac{\sqrt{3}}{2}\\ \tan t=\frac{y}{x}=\frac{\frac{1}{2}}{-\frac{\sqrt{3}}{2}}=\frac{1}{2}\left(-\frac{2}{\sqrt{3}}\right)=-\frac{1}{\sqrt{3}}=-\frac{\sqrt{3}}{3}\\ \sec t=\frac{1}{x}=\frac{1}{\frac{-\frac{\sqrt{3}}{2}}{}}=-\frac{2}{\sqrt{3}}=-\frac{2\sqrt{3}}{3}\\ \csc t=\frac{1}{y}=\frac{1}{\frac{1}{2}}=2\\ \cot t=\frac{x}{y}=\frac{-\frac{\sqrt{3}}{2}}{\frac{1}{2}}=-\frac{\sqrt{3}}{2}\left(\frac{2}{1}\right)=-\sqrt{3}\end{gathered}$

Try It

The point $\left(\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2}\right)$ is on the unit circle, as shown in Figure 3. Find $\sin t,\cos t,\tan t,\sec t,\csc t$, and $\cot t$.

Figure 3

Show Solution

$\sin t=-\frac{\sqrt{2}}{2},\cos t=\frac{\sqrt{2}}{2},\tan t=-1,\sec t=\sqrt{2},\csc t=-\sqrt{2},\cot t=-1$

Because we know the sine and cosine values for the common first-quadrant angles, we can find the other function values for those angles as well by setting $x$ equal to the cosine and $y$ equal to the sine and then using the definitions of tangent, secant, cosecant, and cotangent. The results are shown in the table below.

Using Even and Odd Trigonometric Functions

To be able to use our six trigonometric functions freely with both positive and negative angle inputs, we should examine how each function treats a negative input. As it turns out, there is an important difference among the functions in this regard.

Consider the function $f\left(x\right)={x}^{2}$, shown in Figure 5. The graph of the function is symmetrical about the y-axis. All along the curve, any two points with opposite x-values have the same function value. This matches the result of calculation: ${\left(4\right)}^{2}={\left(-4\right)}^{2}$, ${\left(-5\right)}^{2}={\left(5\right)}^{2}$, and so on. So $f\left(x\right)={x}^{2}$ is an even function, a function such that two inputs that are opposites have the same output. That means $f\left(-x\right)=f\left(x\right)$.

Figure 5. The function $f\left(x\right)={x}^{2}$ is an even function.

Now consider the function $f\left(x\right)={x}^{3}$, shown in Figure 6. The graph is not symmetrical about the y-axis. All along the graph, any two points with opposite x-values also have opposite y-values. So $f\left(x\right)={x}^{3}$ is an odd function, one such that two inputs that are opposites have outputs that are also opposites. That means $f\left(-x\right)=-f\left(x\right)$.

Figure 6. The function $f\left(x\right)={x}^{3}$ is an odd function.

We can test whether a trigonometric function is even or odd by drawing a unit circle with a positive and a negative angle, as in Figure 7. The sine of the positive angle is $y$. The sine of the negative angle is −y. The sine function, then, is an odd function. We can test each of the six trigonometric functions in this fashion. The results are shown in in the table below.

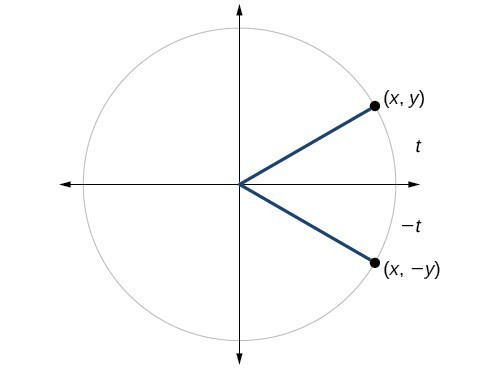
Figure 7

Periodic Properties

If you add or subtract one revolution $\left(360^\circ \text{ or }2\pi\right)$ to an angle, the result will be the same because going around one full revolution will result in the same place on the unit circle. We will let $k$ be any integer, and this represents $k$ revolution in the equations below. These formulas are presented in radians, however they can also be expressed in degrees if we use $360^\circ k$.

Section 4.2 Homework Exercises

1. Describe the unit circle.

2. What do the x- and y-coordinates of the points on the unit circle represent?

3. On an interval of $\left[0,2\pi \right)$, can the sine and cosine values of a radian measure ever be equal? If so, where?

4. What would you estimate the cosine of $\pi$ degrees to be? Explain your reasoning.

5. For any angle in quadrant II, if you knew the sine of the angle, how could you determine the cosine of the angle?

For the following exercises, use the given signs of the trigonometric functions to find the quadrant in which the terminal point determined by $t$ lies.

6. $\text{tan}\left(t\right)>0$ and $\cos \left(t\right)<0$ 7. $\text{tan}\left(t\right)>0$ and $\cos \left(t\right)>0$

8. $\tan \left(t\right)<0$ and $\cos \left(t\right)<0$ 9. $\tan \left(t\right)<0$ and $\cos \left(t\right)>0$

For the following exercises, find the exact value of each trigonometric function.

10. $\sin \frac{\pi }{2}$, $\tan \frac{\pi }{6}$

11. $\sin \frac{\pi }{3}$, $\sec \frac{\pi }{6}$

12. $\cos \frac{\pi }{2}$, $\csc \frac{\pi }{6}$

13. $\cos \frac{\pi }{3}$, $\csc \frac{\pi }{6}$

14. $\sin \frac{\pi }{4}$, $\sec \frac{\pi }{6}$

15. $\cos \frac{\pi }{4}$, $\cot \frac{\pi }{6}$

16. $\sin \frac{\pi }{6}$, $\tan \frac{\pi }{4}$

17. $\sin \pi$, $\sec \frac{\pi }{4}$

18. $\sin \frac{3\pi }{2}$, $\csc \frac{\pi }{4}$

19. $\cos \pi$, $\tan \pi$

20. $\cos \frac{\pi }{6}$, $\sec \frac{\pi }{3}$

21. $\cos 0$, $\tan 0$

For the following exercises, find the requested value.

22. If $\text{cos}\left(t\right)=\frac{1}{7}$ and $t$ is in the 4th quadrant, find $\text{sin}\left(t\right)$.

23. If $\text{cos}\left(t\right)=\frac{2}{9}$ and $t$ is in the 1st quadrant, find $\text{sin}\left(t\right)$.

24. If $\text{sin}\left(t\right)=\frac{3}{8}$ and $t$ is in the 2nd quadrant, find $\text{cos}\left(t\right)$.

25. If $\text{sin}\left(t\right)=-\frac{1}{4}$ and $t$ is in the 3rd quadrant, find $\text{cos}\left(t\right)$.

For the following exercises, use the given point on the unit circle to find the value of all six trigonometric functions of $t$.

26. $\left(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}\right)$

27. $\left(-\frac{\sqrt{3}}{2},\frac{1}{2}\right)$

28. $\left(\frac{1}{2},-\frac{\sqrt{3}}{2}\right)$

29. $\left(-\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2}\right)$

30. $\left(\frac{1}{2},\frac{\sqrt{3}}{2}\right)$

31. $\left(-\frac{1}{2},\frac{\sqrt{3}}{2}\right)$

32. $\left(-\frac{1}{2},-\frac{\sqrt{3}}{2}\right)$

33. $\left(\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2}\right)$

34. $\left(1,0\right)$

35. $\left(-1,0\right)$

36. $\left(0.111,0.994\right)$

37. $\left(0.803,-0.596\right)$

For the following exercises, use a graphing calculator to evaluate.

38. $\sin\left(\frac{5\pi}{9}\right)$

39. $\cos\left(\frac{5\pi}{9}\right)$

40. $\sin\left(18^\circ\right)$

41. $\cos\left(18^\circ\right)$

42. $\sin\left(135^\circ\right)$

43. $\cos\left(135^\circ\right)$

44. $\csc\left(\frac{5\pi }{9}\right)$

45. $\cot\left(\frac{4\pi }{7}\right)$

46. $\sec\left(\frac{\pi }{10}\right)$

47. $\tan\left(\frac{5\pi }{8}\right)$

48. $\cot\left(140^\circ\right)$

49. $\sec\left(310^\circ\right)$

For the following exercises, find the exact value.

50. $\sin\left(\frac{7\pi}{4}\right)\cos\left(\frac{2\pi}{3}\right)$

51. $\sin\left(\frac{3\pi}{4}\right)\cos\left(\frac{5\pi}{3}\right)$

52. $\sin\left(\frac{-4\pi}{3}\right)\cos\left(\frac{\pi}{2}\right)$

53. $\sin\left(\frac{-9\pi}{4}\right)\cos\left(\frac{-\pi}{6}\right)$

54. $\sin\left(\frac{\pi}{6}\right)\cos\left(\frac{-\pi}{3}\right)$

55. $\sin\left(\frac{7\pi}{4}\right)\cos\left(\frac{-2\pi}{3}\right)$

56. $\cos\left(\frac{5\pi}{6}\right)\cos\left(\frac{2\pi}{3}\right)$

57. $\cos\left(\frac{-\pi}{3}\right)\cos\left(\frac{\pi}{4}\right)$

58. $\sin\left(\frac{-5\pi}{4}\right)\sin\left(\frac{11\pi}{6}\right)$

59. $\sin\left(\pi\right)\sin\left(\frac{\pi}{6}\right)$

60. Use the Even-Odd Properties and Periodic Properties to simplify: $5\cos\left(3t+2\pi\right)+\sin(-5t)-\cos\left(-3t\right)$

61. Use the Even-Odd Properties and Periodic Properties to simplify: $2\cos\left(6t+2\pi\right)+\sin(-9t)-\cos\left(-6t\right)$

62. Determine whether the function $f\left(x\right)=2\sin x\cos x$ is even, odd, or neither.

63. Determine whether the function $f\left(x\right)=3{\sin }^{2}x\cos x+\sec x$ is even, odd, or neither.

64. Determine whether the function $f\left(x\right)=\sin x - 2{\cos }^{2}x$ is even, odd, or neither.

65. Determine whether the function $f\left(x\right)={\csc }^{2}x+\sec x$ is even, odd, or neither.

66. The amount of sunlight in a certain city can be modeled by the function $h=15\cos \left(\frac{1}{600}d\right)$, where $h$ represents the hours of sunlight, and $d$ is the day of the year. Use the equation to find how many hours of sunlight there are on February 10, the 42^nd day of the year. State the period of the function.

67. The amount of sunlight in a certain city can be modeled by the function $h=16\cos \left(\frac{1}{500}d\right)$, where $h$ represents the hours of sunlight, and $d$ is the day of the year. Use the equation to find how many hours of sunlight there are on September 24, the 267^th day of the year. State the period of the function.

68. The equation $P=20\sin \left(2\pi t\right)+100$ models the blood pressure, $P$, where $t$ represents time in seconds. (a) Find the blood pressure after 15 seconds. (b) What are the maximum and minimum blood pressures?

69. The height of a piston, $h$, in inches, can be modeled by the equation $y=2\cos x+6$, where $x$ represents the crank angle. Find the height of the piston when the crank angle is $55^\circ$.

70. The height of a piston, $h$, in inches, can be modeled by the equation $y=2\cos x+5$, where $x$ represents the crank angle. Find the height of the piston when the crank angle is $55^\circ$.