In this module, we came a few steps closer to solving the $1,000,000 question by learning some of the basic principles of systems of equations. We learned that using systems of linear equations with two variables allows us to describe relationships that are affected by a number of variables. We saw that graphing systems  is the same as graphing single equations, and that the solution to a system of two linear equations is the point where the two lines intersect.  The number of practical applications for systems of equations spans nearly all disciplines from geology to business to economics to engineering and beyond. For example, electrical engineers may be interested in defining the strength of a current flowing through a circuit as shown in the diagram below.

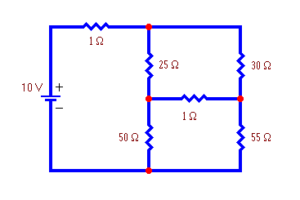
Electrical Circuit

A system of equations based on Kirchoff’s Voltage Law can be constructed and solved to find the current in amperes that flows through each branch of the circuit. Kirchoff’s Voltage Law is based on the principle that voltage changes in intensity as it moves around a circuit. Each equation in the system represents one branch of the circuit, so the number of equations needed to find the current depends on the number of branches in the circuit.  For example, the figure below depicts the circuit from above with it’s three loop currents identified:

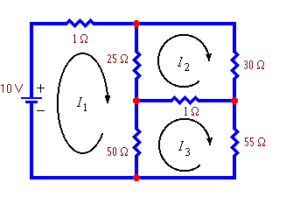
Electrical Circuit With 3 Loop Currents

Because there are three loop currents, we would need to write three equations with three variables based on Kirchoff’s Law to find the three unknown currents that comprise the system. If you are curious to learn more about Kirchoff’s Law and loop currents, visit this site.

If you continue to take more math courses, you may learn how to solve systems of three equations, and may even get to take an entire course in systems called Linear Algebra. And from there you can discover more about the Navier-Stokes equations and, perhaps, solve one of the seven most important math problems in the world!