Curved antennas, such as the ones shown in the photo, are commonly used to focus microwaves and radio waves to transmit television and telephone signals, as well as satellite and spacecraft communication. The cross-section of the antenna is in the shape of a parabola, which can be described by a quadratic function.

An array of satellite dishes. (credit: Matthew Colvin de Valle, Flickr)

(10.2.1) – Identify characteristics of a parabola

The graph of a quadratic function is a U-shaped curve called a parabola. One important feature of the graph is that it has an extreme point, called the vertex. If the parabola opens up, the vertex represents the lowest point on the graph, or the minimum value of the quadratic function. If the parabola opens down, the vertex represents the highest point on the graph, or the maximum value. In either case, the vertex is a turning point on the graph. The graph is also symmetric with a vertical line drawn through the vertex, called the axis of symmetry.

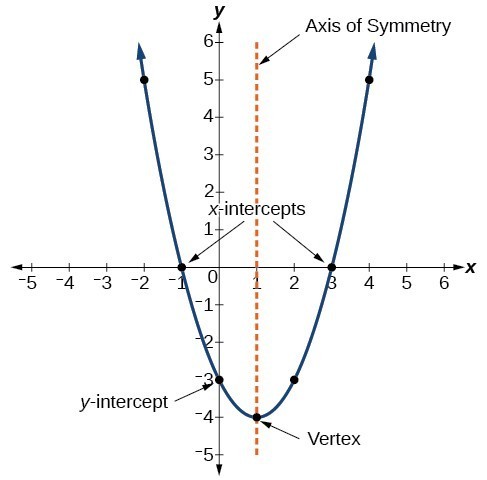
The [latex]y[/latex]-intercept is the point at which the parabola crosses the [latex]y[/latex]-axis. The [latex]x[/latex]-intercepts are the points at which the parabola crosses the [latex]x[/latex]-axis. If they exist, the [latex]x[/latex]-intercepts represent the zeros, or roots, of the quadratic function, the values of [latex]x[/latex] at which [latex]y=0[/latex].

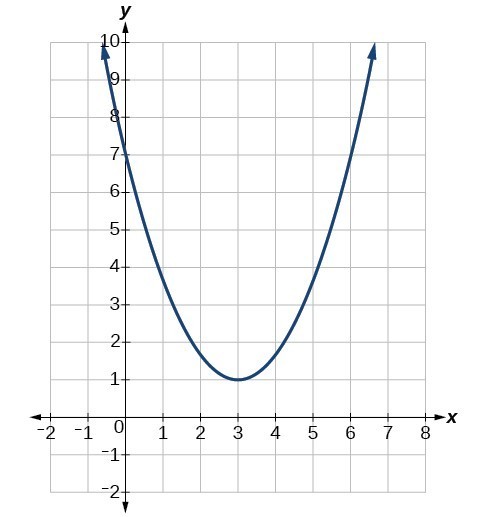
Example: Identifying the Characteristics of a Parabola

Determine the vertex, axis of symmetry, zeros, and y-intercept of the parabola shown below.

Solution

The vertex is the turning point of the graph. We can see that the vertex is at [latex](3,1)[/latex]. Because this parabola opens upward, the axis of symmetry is the vertical line that intersects the parabola at the vertex. So the axis of symmetry is [latex]x=3[/latex]. This parabola does not cross the [latex]x[/latex]-axis, so it has no zeros. It crosses the [latex]y[/latex]-axis at [latex](0, 7)[/latex] so this is the [latex]y[/latex]-intercept.

General and Standard Forms of Quadratic Functions

The general form of a quadratic function presents the function in the form

[latex]f\left(x\right)=a{x}^{2}+bx+c[/latex]

where [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] are real numbers and [latex]a\ne 0[/latex]. If [latex]a>0[/latex], the parabola opens upward. If [latex]a<0[/latex], the parabola opens downward. We can use the general form of a parabola to find the equation for the axis of symmetry.

The axis of symmetry is defined by [latex]\displaystyle x=-\frac{b}{2a}[/latex]. If we use the quadratic formula, [latex]\displaystyle x=\frac{-b\pm \sqrt{{b}^{2}-4ac}}{2a}[/latex], to solve [latex]a{x}^{2}+bx+c=0[/latex] for the [latex]x[/latex]-intercepts, or zeros, we find the value of [latex]x[/latex] halfway between them is always [latex]\displaystyle x=-\frac{b}{2a}[/latex], the equation for the axis of symmetry.

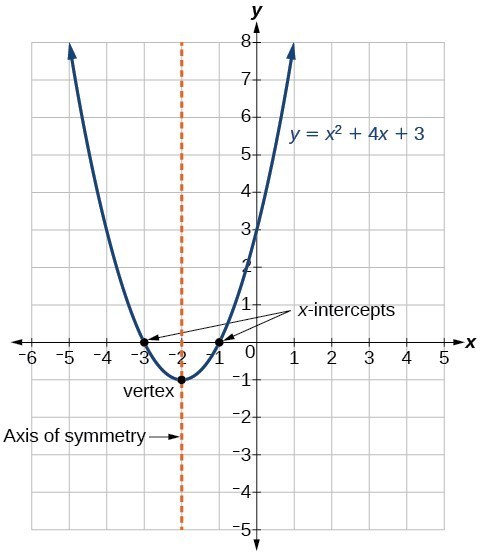
The figure below shows the graph of the quadratic function written in general form as [latex]y={x}^{2}+4x+3[/latex]. In this form, [latex]a=1,\text{ }b=4[/latex], and [latex]c=3[/latex]. Because [latex]a>0[/latex], the parabola opens upward. The axis of symmetry is [latex]\displaystyle x=-\frac{4}{2\left(1\right)}=-2[/latex]. This also makes sense because we can see from the graph that the vertical line [latex]x=-2[/latex] divides the graph in half. The vertex always occurs along the axis of symmetry. For a parabola that opens upward, the vertex occurs at the lowest point on the graph, in this instance, [latex]\left(-2,-1\right)[/latex]. The [latex]x[/latex]-intercepts, those points where the parabola crosses the [latex]x[/latex]-axis, occur at [latex]\left(-3,0\right)[/latex] and [latex]\left(-1,0\right)[/latex].

The standard form of a quadratic function presents the function in the form

[latex]f\left(x\right)=a{\left(x-h\right)}^{2}+k[/latex]

where [latex]\left(h,\text{ }k\right)[/latex] is the vertex. Because the vertex appears in the standard form of the quadratic function, this form is also known as the vertex form of a quadratic function.

Given a quadratic function in general form, find the vertex of the parabola.

One reason we may want to identify the vertex of the parabola is that this point will inform us where the maximum or minimum value of the output occurs, ([latex]k[/latex]), and where it occurs, ([latex]x[/latex]). If we are given the general form of a quadratic function:

[latex]f(x)=ax^2+bx+c[/latex]

We can define the vertex, [latex](h,k)[/latex], by doing the following:

• Identify [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex].
• Find [latex]h[/latex], the [latex]x[/latex]-coordinate of the vertex, by substituting [latex]a[/latex] and [latex]b[/latex] into [latex]\displaystyle h=-\frac{b}{2a}[/latex].
• Find [latex]k[/latex], the [latex]y[/latex]-coordinate of the vertex, by evaluating [latex]\displaystyle k=f\left(h\right)=f\left(-\frac{b}{2a}\right)[/latex]

In this section, we will investigate quadratic functions further, including solving problems involving area and projectile motion. Working with quadratic functions can be less complex than working with higher degree polynomial functions, so they provide a good opportunity for a detailed study of function behavior.

(10.2.2) – Classifying Solutions to Quadratic Equations

Much as we did in the application problems above, we also need to find intercepts of quadratic equations for graphing parabolas. Recall that we find the y-intercept of a quadratic by evaluating the function at an input of zero, and we find the x-intercepts at locations where the output is zero. Notice that the number of x-intercepts can vary depending upon the location of the graph.

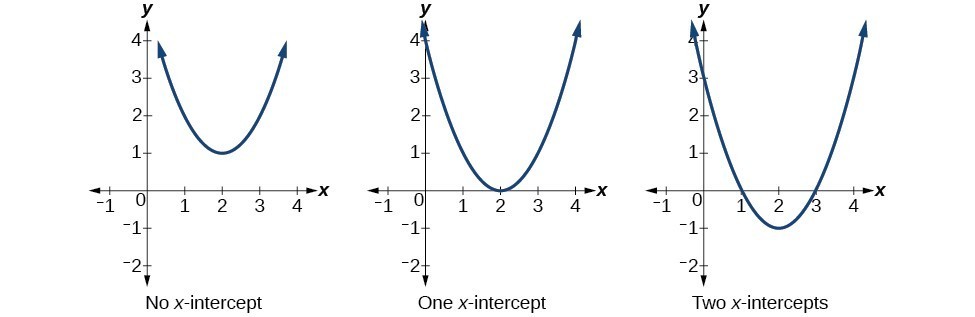
Number of x-intercepts of a parabola

Mathematicians also define x-intercepts as roots of the quadratic function.

Example: Finding the [latex]y[/latex]– and [latex]x[/latex]-Intercepts of a Parabola

Find the [latex]y[/latex]– and [latex]x[/latex]-intercepts of the quadratic [latex]f\left(x\right)=3{x}^{2}+5x - 2[/latex].

Solution

We find the [latex]y[/latex]-intercept by evaluating [latex]f\left(0\right)[/latex].

[latex]\begin{array}{c}f\left(0\right)=3{\left(0\right)}^{2}+5\left(0\right)-2\hfill \\ \text{ }=-2\hfill \end{array}[/latex]

So the [latex]y[/latex]-intercept is at [latex]\left(0,-2\right)[/latex].

For the [latex]x[/latex]-intercepts, or roots, we find all solutions of [latex]f\left(x\right)=0[/latex].

[latex]0=3{x}^{2}+5x - 2[/latex]

In this case, the quadratic can be factored easily, providing the simplest method for solution.

[latex]0=\left(3x - 1\right)\left(x+2\right)[/latex]
[latex]\begin{array}{c}0=3x - 1\hfill & \hfill & \hfill & \hfill & 0=x+2\hfill \\ x=\frac{1}{3}\hfill & \hfill & \text{or}\hfill & \hfill & x=-2\hfill \end{array}[/latex]

So the roots are at [latex]\left(\frac{1}{3},0\right)[/latex] and [latex]\left(-2,0\right)[/latex].

Analysis of the Solution

By graphing the function, we can confirm that the graph crosses the y-axis at [latex]\left(0,-2\right)[/latex]. We can also confirm that the graph crosses the [latex]x[/latex]-axis at [latex]\left(\frac{1}{3},0\right)[/latex] and [latex]\left(-2,0\right)[/latex].

In the previous example, finding the [latex]y[/latex]– and [latex]x[/latex]-Intercepts of a parabola, the quadratic was easily solved by factoring. However, there are many quadratics that cannot be factored. We can solve these quadratics by first rewriting them in standard form.

Example: Finding the Roots of a Parabola

Find the [latex]x[/latex]-intercepts of the quadratic function [latex]f\left(x\right)=2{x}^{2}+4x - 4[/latex].

Solution

We begin by solving for when the output will be zero.

[latex]0=2{x}^{2}+4x - 4[/latex]

Because the quadratic is not easily factorable in this case, we solve for the intercepts by first rewriting the quadratic in standard form.

[latex]f\left(x\right)=a{\left(x-h\right)}^{2}+k[/latex]

We know that [latex]a=2[/latex]. Then we solve for [latex]h[/latex] and [latex]k[/latex].

[latex]\large \begin{array}{c}h=-\frac{b}{2a}\hfill & \hfill & \hfill & k=f\left(-1\right)\hfill \\ \text{ }=-\frac{4}{2\left(2\right)}\hfill & \hfill & \hfill & \text{ }=2{\left(-1\right)}^{2}+4\left(-1\right)-4\hfill \\ \text{ }=-1\hfill & \hfill & \hfill & \text{ }=-6\hfill \end{array}[/latex]

So now we can rewrite in standard form.

[latex]f\left(x\right)=2{\left(x+1\right)}^{2}-6[/latex]

We can now solve for when the output will be zero.

[latex]\begin{array}{c}0=2{\left(x+1\right)}^{2}-6\hfill \\ 6=2{\left(x+1\right)}^{2}\hfill \\ 3={\left(x+1\right)}^{2}\hfill \\ x+1=\pm \sqrt{3}\hfill \\ x=-1\pm \sqrt{3}\hfill \end{array}[/latex]

The graph has [latex]x[/latex]–intercepts at [latex]\left(-1-\sqrt{3},0\right)[/latex] and [latex]\left(-1+\sqrt{3},0\right)[/latex].

Analysis of the Solution

We can check our work by graphing the given function on a graphing utility and observing the roots.

Complex Roots

Now you will hopefully begin to understand why we introduced complex numbers at the beginning of this module. Consider the following function: [latex]f(x)=x^2+2x+3[/latex], and it’s graph below:

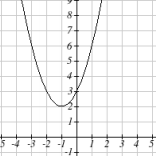
Does this function have roots? It’s probably obvious that this function does not cross the [latex]x[/latex]-axis, therefore it doesn’t have any [latex]x[/latex]-intercepts. Recall that the [latex]x[/latex]-intercepts of a function are found by setting the function equal to zero:

[latex]x^2+2x+3=0[/latex]

In the next example, we will solve this equation.  You will see that there are roots, but they are not [latex]x[/latex]-intercepts because the function does not contain [latex](x,y)[/latex] pairs that are on the [latex]x[/latex]-axis.  We call these complex roots.

By setting the function equal to zero and using the quadratic formula to solve, you will see that the roots contain complex numbers:

[latex]x^2+2x+3=0[/latex]

Example

Find the [latex]x[/latex]-intercepts of the quadratic function. [latex]f(x)=x^2+2x+3[/latex]

Show Answer

The [latex]x[/latex]-intercepts of the function [latex]f(x)=x^2+2x+3[/latex] are found by setting it equal to zero, and solving for [latex]x[/latex] since the [latex]y[/latex] values of the [latex]x[/latex]-intercepts are zero.

First, identify [latex]a[/latex], [latex]b[/latex], [latex]c[/latex].

[latex]\begin{array}{ccc}x^2+2x+3=0\\a=1,b=2,c=3\end{array}[/latex]

Substitute these values into the quadratic formula.

[latex]\large \begin{array}{c}x&=&\frac{-b\pm \sqrt{{b}^{2}-4ac}}{2a}\\&=&\frac{-2\pm \sqrt{{2}^{2}-4(1)(3)}}{2(1)}\\&=&\frac{-2\pm \sqrt{4-12}}{2} \\&=&\frac{-2\pm \sqrt{-8}}{2}\\&=&\frac{-2\pm 2i\sqrt{2}}{2} \\-1\pm i\sqrt{2}&=&-1+\sqrt{2},-1-\sqrt{2}\end{array}[/latex]

The solutions to this equations are complex, therefore there are no [latex]x[/latex]-intercepts for the function [latex]f(x)=x^2+2x+3[/latex] in the set of real numbers that can be plotted on the Cartesian Coordinate plane. The graph of the function is plotted on the Cartesian Coordinate plane below:

Graph of quadratic function with no x-intercepts in the real numbers.

Note how the graph does not cross the [latex]x[/latex]-axis, therefore there are no real [latex]x[/latex]-intercepts for this function.

Important Terms

axis of symmetry

a vertical line drawn through the vertex of a parabola around which the parabola is symmetric; it is defined by [latex]\displaystyle x=-\frac{b}{2a}[/latex].

general form of a quadratic function

the function that describes a parabola, written in the form [latex]f\left(x\right)=a{x}^{2}+bx+c[/latex], where [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] are real numbers and [latex]a\ne 0[/latex].

standard form of a quadratic function

the function that describes a parabola, written in the form [latex]f\left(x\right)=a{\left(x-h\right)}^{2}+k[/latex], where [latex]\left(h,\text{ }k\right)[/latex] is the vertex.

vertex

the point at which a parabola changes direction, corresponding to the minimum or maximum value of the quadratic function

zeros

in a given function, the values of [latex]x[/latex] at which [latex]y = 0[/latex], also called roots