Learning Objectives
- (4.3.1) – Write down equations of parallel and perpendicular lines
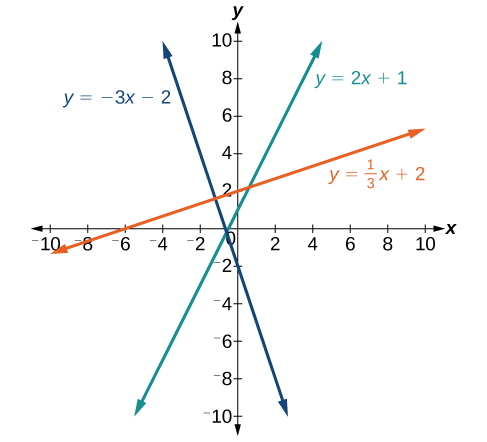
Below are some graphs of lines. Recall, if the slope is positive, the line slants to the right. If the slope is negative, the line slants to the left. As the slope increases, the line becomes steeper. The lines indicate the following slopes: [latex]m=-3[/latex], [latex]m=2[/latex], and [latex]m=\frac{1}{3}[/latex].
(4.3.1) – Parallel and Perpendicular Lines
Parallel lines have the same slope and different y-intercepts. Lines that are parallel to each other will never intersect. For example, the figure below shows the graphs of various lines with the same slope, [latex]m=2[/latex].
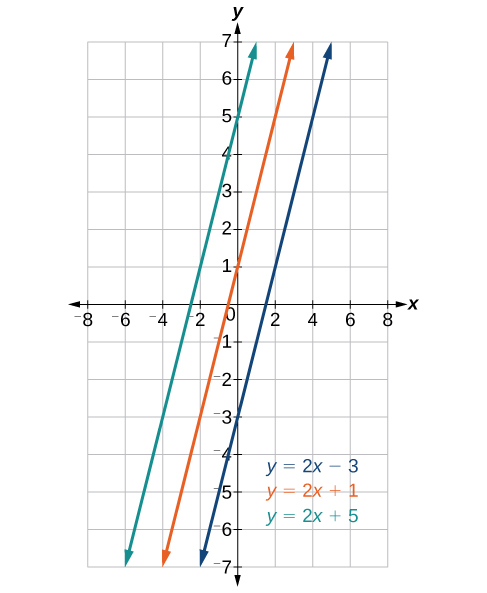
Parallel lines
All of the lines shown in the graph are parallel because they have the same slope and different y-intercepts.
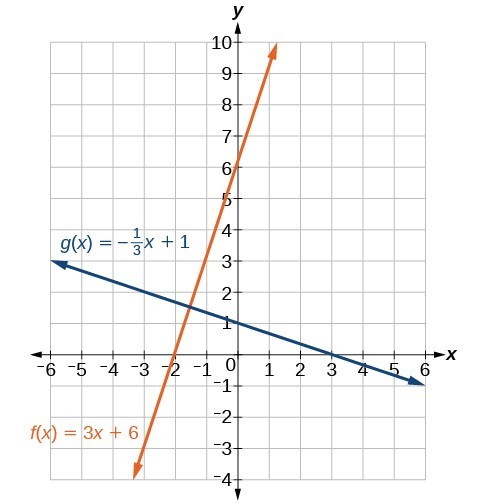
Lines that are perpendicular intersect to form a [latex]{90}^{\circ }[/latex] -angle. The slope of one line is the negative reciprocal of the other. We can show that two lines are perpendicular if the product of the two slopes is [latex]-1:{m}_{1}\cdot {m}_{2}=-1[/latex]. For example, the figure above shows the graph of two perpendicular lines. One line has a slope of 3; the other line has a slope of [latex]-\frac{1}{3}[/latex].
[latex]\begin{array}{l}\text{ }{m}_{1}\cdot {m}_{2}=-1\hfill \\ \text{ }3\cdot \left(-\frac{1}{3}\right)=-1\hfill \end{array}[/latex]
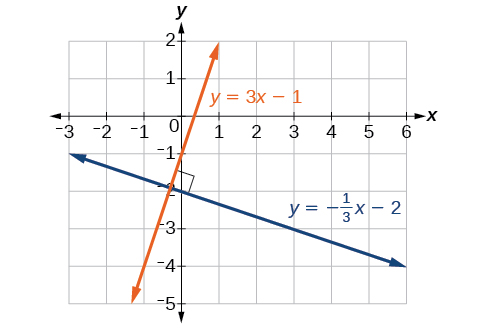
Perpendicular lines
Example: Graphing Two Equations, and Determining Whether the Lines are Parallel, Perpendicular, or Neither
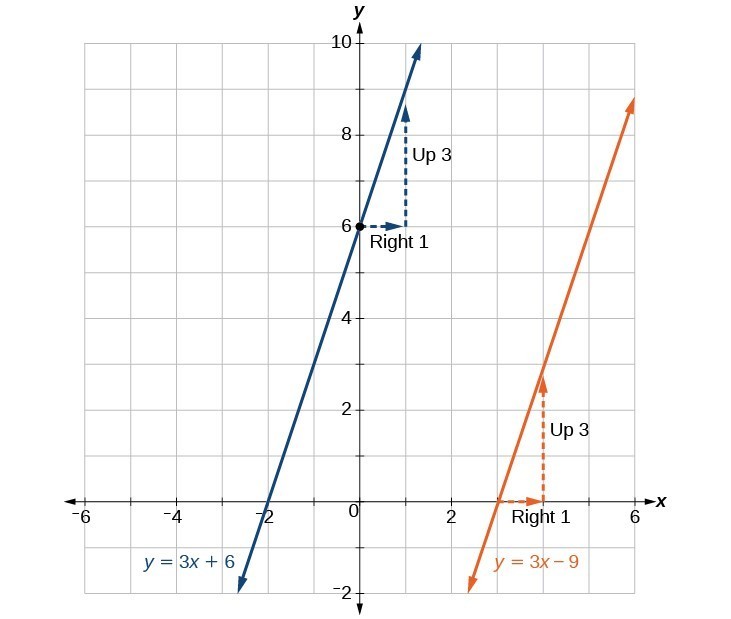
Graph the equations of the given lines, and state whether they are parallel, perpendicular, or neither: [latex]3y=-4x+3[/latex] and [latex]3x - 4y=8[/latex].
Try It
Graph the two lines and determine whether they are parallel, perpendicular, or neither: [latex]2y-x=10[/latex] and [latex]2y=x+4[/latex].
If we know the equation of a line, we can use what we know about slope to write the equation of a line that is either parallel or perpendicular to the given line.
Writing Equations of Parallel Lines
Suppose for example, we are given the following equation.
[latex]f\left(x\right)=3x+1[/latex]
We know that the slope of the line formed by the function is 3. We also know that the y-intercept is (0, 1). Any other line with a slope of 3 will be parallel to f(x). So the lines formed by all of the following functions will be parallel to f(x).
[latex]\begin{cases}g\left(x\right)=3x+6\hfill \\ h\left(x\right)=3x+1\hfill \\ p\left(x\right)=3x+\frac{2}{3}\hfill \end{cases}[/latex]
Suppose then we want to write the equation of a line that is parallel to f and passes through the point (1, 7). We already know that the slope is 3. We just need to determine which value for b will give the correct line. We can begin with the point-slope form of an equation for a line, and then rewrite it in the slope-intercept form.
[latex]\begin{cases}y-{y}_{1}=m\left(x-{x}_{1}\right)\hfill \\ y - 7=3\left(x - 1\right)\hfill \\ y - 7=3x - 3\hfill \\ \text{ }y=3x+4\hfill \end{cases}[/latex]
So [latex]g\left(x\right)=3x+4[/latex] is parallel to [latex]f\left(x\right)=3x+1[/latex] and passes through the point (1, 7).
How To: Given the equation of a function and a point through which its graph passes, write the equation of a line parallel to the given line that passes through the given point.
- Find the slope of the function.
- Substitute the given values into either the general point-slope equation or the slope-intercept equation for a line.
- Simplify.
Example: Finding a Line Parallel to a Given Line
Find a line parallel to the graph of [latex]f\left(x\right)=3x+6[/latex] that passes through the point (3, 0).
Try It
Writing Equations of Perpendicular Lines
We can use a very similar process to write the equation for a line perpendicular to a given line. Instead of using the same slope, however, we use the negative reciprocal of the given slope. Suppose we are given the following function:
[latex]f\left(x\right)=2x+4[/latex]
The slope of the line is 2, and its negative reciprocal is [latex]-\frac{1}{2}[/latex]. Any function with a slope of [latex]-\frac{1}{2}[/latex] will be perpendicular to f(x). So the lines formed by all of the following functions will be perpendicular to f(x).
[latex]\begin{cases}g\left(x\right)=-\frac{1}{2}x+4\hfill \\ h\left(x\right)=-\frac{1}{2}x+2\hfill \\ p\left(x\right)=-\frac{1}{2}x-\frac{1}{2}\hfill \end{cases}[/latex]
As before, we can narrow down our choices for a particular perpendicular line if we know that it passes through a given point. Suppose then we want to write the equation of a line that is perpendicular to f(x) and passes through the point (4, 0). We already know that the slope is [latex]-\frac{1}{2}[/latex]. Now we can use the point to find the y-intercept by substituting the given values into the slope-intercept form of a line and solving for b.
[latex]\begin{cases}g\left(x\right)=mx+b\hfill \\ 0=-\frac{1}{2}\left(4\right)+b\hfill \\ 0=-2+b\hfill \\ 2=b\hfill \\ b=2\hfill \end{cases}[/latex]
The equation for the function with a slope of [latex]-\frac{1}{2}[/latex] and a y-intercept of 2 is [latex]g\left(x\right)=-\frac{1}{2}x+2[/latex].
So [latex]g\left(x\right)=-\frac{1}{2}x+2[/latex] is perpendicular to [latex]f\left(x\right)=2x+4[/latex] and passes through the point (4, 0). Be aware that perpendicular lines may not look obviously perpendicular on a graphing calculator unless we use the square zoom feature.
Q & A
A horizontal line has a slope of zero and a vertical line has an undefined slope. These two lines are perpendicular, but the product of their slopes is not –1. Doesn’t this fact contradict the definition of perpendicular lines?
No. For two perpendicular linear functions, the product of their slopes is –1. However, a vertical line is not a function so the definition is not contradicted.
How To: Given the equation of a function and a point through which its graph passes, write the equation of a line perpendicular to the given line.
- Find the slope of the function.
- Determine the negative reciprocal of the slope.
- Substitute the new slope and the values for x and y from the coordinate pair provided into [latex]g\left(x\right)=mx+b[/latex].
- Solve for b.
- Write the equation for the line.
Example: Finding the Equation of a Perpendicular Line
Find the equation of a line perpendicular to [latex]y=3x+3[/latex] that passes through the point (3, 0).
Try It
Given the line [latex]y=2x - 4[/latex], write an equation for the line passing through (0, 0) that is
- parallel to y
- perpendicular to y
How To: Given two points on a line and a third point, write the equation of the perpendicular line that passes through the point.
- Determine the slope of the line passing through the points.
- Find the negative reciprocal of the slope.
- Use the slope-intercept form or point-slope form to write the equation by substituting the known values.
- Simplify.
Example: Finding the Equation of a Line Perpendicular to a Given Line Passing through a Point
A line passes through the points (–2, 6) and (4, 5). Find the equation of a perpendicular line that passes through the point (4, 5).
Try It
A line passes through the points, (–2, –15) and (2, –3). Find the equation of a perpendicular line that passes through the point, (6, 4).
Writing the Equations of Lines Parallel or Perpendicular to a Given Line
As we have learned, determining whether two lines are parallel or perpendicular is a matter of finding the slopes. To write the equation of a line parallel or perpendicular to another line, we follow the same principles as we do for finding the equation of any line. After finding the slope, use the point-slope formula to write the equation of the new line.
How To: Given an equation for a line, write the equation of a line parallel or perpendicular to it.
- Find the slope of the given line. The easiest way to do this is to write the equation in slope-intercept form.
- Use the slope and the given point with the point-slope formula.
- Simplify the line to slope-intercept form and compare the equation to the given line.
Example: Writing the Equation of a Line Parallel to a Given Line Passing Through a Given Point
Write the equation of line parallel to a [latex]5x+3y=1[/latex] and passing through the point [latex]\left(3,5\right)[/latex].
Try It
Find the equation of the line parallel to [latex]5x=7+y[/latex] and passing through the point [latex]\left(-1,-2\right)[/latex].
Example: Finding the Equation of a Line Perpendicular to a Given Line Passing Through a Given Point
Find the equation of the line perpendicular to [latex]5x - 3y+4=0[/latex] and passing through the point [latex](-4,1)[/latex].
Candela Citations
- Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
- College Algebra. Authored by: Abramson, Jay et al.. Provided by: OpenStax. Located at: http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@5.2. License: CC BY: Attribution. License Terms: Download for free at http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@5.2
- Question ID 110942, 110946, 110951, 110952, 110960, 110970, 110971. Authored by: Lumen Learning. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL
- Question ID 1436. Authored by: WebWork-Rochester. License: CC BY: Attribution. License Terms: IMathAS Community License CC- BY + GPL