Learning Objectives
- (9.4.1) – Multiply and divide radical expressions
- Use the product raised to a power rule to multiply radical expressions
- Use the quotient raised to a power rule to divide radical expressions
- (9.4.2) – Add and subtract radical expressions
- (9.4.3) – Multiply radicals with multiple terms
- (9.4.4) – Rationalize a denominator containing a radical expression
- Rationalize denominators with one term
- Rationalize denominators with higher roots
- Rationalize denominators with multiple terms
When you learned how to solve linear equations, you probably learned about like terms first. We can only combine terms that are alike, otherwise the terms will lose their meaning. In this section, when you learn how to perform algebraic operations on radical expressions you will use the concept of like terms in a new way.
You will also use the distributive property, rules for exponents, and methods for multiplying binomials to perform algebraic operations on radical expressions.
(9.4.1) – Multiply and Divide Radical Expressions
You can do more than just simplify radical expressions. You can multiply and divide them, too. The product raised to a power rule that we discussed previously will help us find products of radical expressions. Recall the rule:
Multiply Radical Expressions
A Product Raised to a Power Rule
For any numbers [latex]a[/latex] and [latex]b[/latex] and any integer [latex]n[/latex]: [latex] {{(ab)}^{n}}={{a}^{n}}\cdot {{b}^{n}}[/latex]
For any numbers [latex]a[/latex] and [latex]b[/latex] and any positive integer [latex]n[/latex]: [latex]\large {{(ab)}^{\frac{1}{n}}}={{a}^{\frac{1}{n}}}\cdot {{b}^{\frac{1}{n}}}[/latex]
For any numbers [latex]a[/latex] and [latex]b[/latex] and any positive integer [latex]n[/latex]: [latex] \sqrt[n]{ab}=\sqrt[n]{a}\cdot \sqrt[n]{b}[/latex]
The Product Raised to a Power Rule is important because you can use it to multiply radical expressions. Note that you can’t multiply a square root and a cube root using this rule. The indices of the radicals must match in order to multiply them. In our first example we will work with integers, then we will move on to expressions with variable radicands.
Example
Simplify. [latex] \sqrt{18}\cdot \sqrt{16}[/latex]
You may have also noticed that both [latex] \sqrt{18}[/latex] and [latex] \sqrt{16}[/latex] can be written as products involving perfect square factors. How would the expression change if you simplified each radical first, before multiplying? In the next example we will use the same product from above to show that you can simplify before multiplying and get the same result.
Example
Simplify. [latex] \sqrt{18}\cdot \sqrt{16}[/latex]
In both cases, you arrive at the same product, [latex] 12\sqrt{2}[/latex]. It does not matter whether you multiply the radicands or simplify each radical first.
You multiply radical expressions that contain variables in the same manner. As long as the roots of the radical expressions are the same, you can use the Product Raised to a Power Rule to multiply and simplify. Look at the two examples that follow. In both problems, the Product Raised to a Power Rule is used right away and then the expression is simplified. Note that we specify that the variable is non-negative, [latex] x\ge 0[/latex], thus allowing us to avoid the need for absolute value.
Example
Simplify. [latex] \sqrt{12{{x}^{4}}}\cdot \sqrt{3x^2}[/latex], [latex] x\ge 0[/latex]
In our next example we will multiply two cube roots.
Example
Simplify. [latex] \sqrt[3]{{{x}^{5}}{{y}^{2}}}\cdot 5\sqrt[3]{8{{x}^{2}}{{y}^{4}}}[/latex]
In the following video we present more examples of how to multiply radical expressions.
This next example is slightly more complicated because there are more than two radicals being multiplied. In this case, notice how the radicals are simplified before multiplication takes place. (Remember that the order you choose to use is up to you—you will find that sometimes it is easier to multiply before simplifying, and other times it is easier to simplify before multiplying. With some practice, you may be able to tell which is which before you approach the problem, but either order will work for all problems.)
Example
Simplify. [latex] 2\sqrt[4]{16{{x}^{9}}}\cdot \sqrt[4]{{{y}^{3}}}\cdot \sqrt[4]{81{{x}^{3}}y}[/latex], [latex] x\ge 0[/latex], [latex] y\ge 0[/latex]
In the following video we show more examples of multiplying cube roots.
Dividing Radical Expressions
You can use the same ideas to help you figure out how to simplify and divide radical expressions. Recall that the Product Raised to a Power Rule states that [latex] \sqrt[n]{ab}=\sqrt[n]{a}\cdot \sqrt[n]{b}[/latex]. Well, what if you are dealing with a quotient instead of a product?
There is a rule for that, too. The Quotient Raised to a Power Rule states that [latex]\displaystyle {{\left( \frac{a}{b} \right)}^{n}}=\frac{{{a}^{n}}}{{{b}^{n}}}[/latex]. Again, if you imagine that the exponent is a rational number, then you can make this rule applicable for roots as well: [latex]\displaystyle {{\left( \frac{a}{b} \right)}^{\frac{1}{n}}}=\frac{{{a}^{\frac{1}{n}}}}{{{b}^{\frac{1}{n}}}}[/latex], so [latex]\displaystyle \sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}[/latex].
A Quotient Raised to a Power Rule
For any real numbers [latex]a[/latex] and [latex]b[/latex] ([latex]b \ne 0[/latex]) and any positive integer [latex]n[/latex]: [latex]\large {{\left( \frac{a}{b} \right)}^{\frac{1}{n}}}=\frac{{{a}^{\frac{1}{n}}}}{{{b}^{\frac{1}{n}}}}[/latex]
For any real numbers [latex]a[/latex] and [latex]b[/latex] ([latex]b \ne 0[/latex]) and any positive integer [latex]n[/latex]: [latex]\large \sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}[/latex]
As you did with multiplication, you will start with some examples featuring integers before moving on to more complex expressions like [latex]\displaystyle \frac{\sqrt[3]{24x{{y}^{4}}}}{\sqrt[3]{8y}}[/latex].
Example
Simplify. [latex]\displaystyle \sqrt{\frac{48}{25}}[/latex]
Example
Simplify. [latex]\displaystyle \sqrt[3]{\frac{640}{40}}[/latex]
That was a lot of effort, but you were able to simplify using the Quotient Raised to a Power Rule. What if you found the quotient of this expression by dividing within the radical first, and then took the cube root of the quotient?
Let’s take another look at that problem.
Example
Simplify. [latex]\displaystyle \frac{\sqrt[3]{640}}{\sqrt[3]{40}}[/latex]
That was a more straightforward approach, wasn’t it?
In the next video we show more examples of simplifying a radical that contains a quotient.
As with multiplication, the main idea here is that sometimes it makes sense to divide and then simplify, and other times it makes sense to simplify and then divide. Whichever order you choose, though, you should arrive at the same final expression.
Now let’s turn to some radical expressions containing division. Notice that the process for dividing these is the same as it is for dividing integers.
Example
Simplify. [latex]\displaystyle \frac{\sqrt{30x}}{\sqrt{10x}},x>0[/latex]
Example
Simplify. [latex]\displaystyle \frac{\sqrt[3]{24x{{y}^{4}}}}{\sqrt[3]{8y}},\,\,y\ne 0[/latex]
In our last video we show more examples of simplifying radicals that contain quotients with variables.
As you become more familiar with dividing and simplifying radical expressions, make sure you continue to pay attention to the roots of the radicals that you are dividing. For example, while you can think of [latex]\displaystyle \frac{\sqrt{8{{y}^{2}}}}{\sqrt{225{{y}^{4}}}}[/latex] as equivalent to [latex]\displaystyle \sqrt{\frac{8{{y}^{2}}}{225{{y}^{4}}}}[/latex] since both the numerator and the denominator are square roots, notice that you cannot express [latex]\displaystyle \frac{\sqrt{8{{y}^{2}}}}{\sqrt[4]{225{{y}^{4}}}}[/latex] as [latex]\displaystyle \sqrt[4]{\frac{8{{y}^{2}}}{225{{y}^{4}}}}[/latex]. In this second case, the numerator is a square root and the denominator is a fourth root.
(9.4.2) – Add and Subtract Radical Expressions
There are two keys to combining radicals by addition or subtraction: look at the index, and look at the radicand. If these are the same, then addition and subtraction are possible. If not, then you cannot combine the two radicals. In the graphic below, the index of the expression [latex]12\sqrt[3]{xy}[/latex] is 3 and the radicand is [latex]xy[/latex].
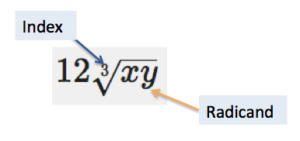
Making sense of a string of radicals may be difficult. One helpful tip is to think of radicals as variables, and treat them the same way. When you add and subtract variables, you look for like terms, which is the same thing you will do when you add and subtract radicals.
Definition
Radical expressions with the same indices and the same radicands are called like radicals.
Adding Radicals
In this first example, both radicals have the same radicand and index.
Example
Add. [latex] 3\sqrt{11}+7\sqrt{11}[/latex]
This next example contains more addends, or terms that are being added together. Notice how you can combine like terms (radicals that have the same root and index) but you cannot combine unlike terms.
Example
Add. [latex] 5\sqrt{2}+\sqrt{3}+4\sqrt{3}+2\sqrt{2}[/latex]
Notice that the expression in the previous example is simplified even though it has two terms: [latex] 7\sqrt{2}[/latex] and [latex] 5\sqrt{3}[/latex]. It would be a mistake to try to combine them further! (Some people make the mistake that [latex] 7\sqrt{2}+5\sqrt{3}=12\sqrt{5}[/latex]. This is incorrect because[latex] \sqrt{2}[/latex] and [latex]\sqrt{3}[/latex] are not like radicals so they cannot be added.)
Example
Add. [latex] 3\sqrt{x}+12\sqrt[3]{xy}+\sqrt{x}[/latex]
In the following video we show more examples of how to identify and add like radicals.
Sometimes you may need to add and simplify the radical. If the radicals are different, try simplifying first—you may end up being able to combine the radicals at the end, as shown in these next two examples.
Example
Add and simplify. [latex] 2\sqrt[3]{40}+\sqrt[3]{135}[/latex]
Example
Add and simplify. [latex] x\sqrt[3]{x{{y}^{4}}}+y\sqrt[3]{{{x}^{4}}y}[/latex]
The following video shows more examples of adding radicals that require simplification.
Subtracting Radicals
Subtraction of radicals follows the same set of rules and approaches as addition—the radicands and the indices must be the same for two (or more) radicals to be subtracted. In the three examples that follow, subtraction has been rewritten as addition of the opposite.
Example
Subtract. [latex] 5\sqrt{13}-3\sqrt{13}[/latex]
Example
Subtract. [latex] 4\sqrt[3]{5a}-\sqrt[3]{3a}-2\sqrt[3]{5a}[/latex]
In the following video we show more examples of subtracting radical expressions when no simplifying is required.
Example
Subtract and simplify. [latex] 5\sqrt[4]{{{a}^{5}}b}-a\sqrt[4]{16ab}[/latex], where [latex]a\ge 0[/latex] and [latex]b\ge 0[/latex]
In our last video we show more examples of subtracting radicals that require simplifying.
(9.4.3) – Multiply radicals with multiple terms
When multiplying multiple term radical expressions it is important to follow the Distributive Property of Multiplication, as when you are multiplying regular, non-radical expressions.
Radicals follow the same mathematical rules that other real numbers do. So, although the expression [latex] \sqrt{x}(3\sqrt{x}-5)[/latex] may look different than [latex] a(3a-5)[/latex], you can treat them the same way.
Let’s have a look at how to apply the Distributive Property. First let’s do a problem with the variable [latex]a[/latex], and then solve the same problem replacing [latex]a[/latex] with [latex] \sqrt{x}[/latex].
Example
Simplify. [latex] a(3a-5)[/latex]
Example
Simplify. [latex] \sqrt{x}(3\sqrt{x}-5)[/latex]
The answers to the previous two problems should look similar to you. The only difference is that in the second problem, [latex] \sqrt{x}[/latex] has replaced the variable [latex]a[/latex] (and so [latex] \left| x \right|[/latex] has replaced [latex]a^2[/latex]). The process of multiplying is very much the same in both problems.
In these next two problems, each term contains a radical.
Example
Simplify. [latex] 7\sqrt{x}\left( 2\sqrt{xy}+\sqrt{y} \right)[/latex]
Example
Simplify. [latex] \sqrt[3]{a}\left( 2\sqrt[3]{{{a}^{2}}}-4\sqrt[3]{{{a}^{5}}}+8\sqrt[3]{{{a}^{8}}} \right)[/latex]
In the following video we show more examples of how to multiply radical expressions using distribution.
In all of these examples, multiplication of radicals has been shown following the pattern [latex] \sqrt{a}\cdot \sqrt{b}=\sqrt{ab}[/latex]. Then, only after multiplying, some radicals have been simplified—like in the last problem. After you have worked with radical expressions a bit more, you may feel more comfortable identifying quantities such as [latex] \sqrt{x}\cdot \sqrt{x}=x[/latex] without going through the intermediate step of finding that [latex] \sqrt{x}\cdot \sqrt{x}=\sqrt{{{x}^{2}}}[/latex]. In the rest of the examples that follow, though, each step is shown.
Multiply Binomial Expressions That Contain Radicals
You can use the same technique for multiplying binomials to multiply binomial expressions with radicals.
As a refresher, here is the process for multiplying two binomials. If you like using the expression “FOIL” (First, Outside, Inside, Last) to help you figure out the order in which the terms should be multiplied, you can use it here, too.
Example
Multiply. [latex] \left( 2x+5 \right)\left( 3x-2 \right)[/latex]
Here is the same problem, with [latex] \sqrt{b}[/latex] replacing the variable [latex]x[/latex].
Example
Multiply. [latex] \left( 2\sqrt{b}+5 \right)\left( 3\sqrt{b}-2 \right),\,\,b\ge 0[/latex]
The multiplication works the same way in both problems; you just have to pay attention to the index of the radical (that is, whether the roots are square roots, cube roots, etc.) when multiplying radical expressions.
Multiplying Two-Term Radical Expressions
To multiply radical expressions, use the same method as used to multiply polynomials.
- Use the Distributive Property (or, if you prefer, the shortcut FOIL method);
- Remember that [latex] \sqrt{a}\cdot \sqrt{b}=\sqrt{ab}[/latex]; and
- Combine like terms.
Example
Multiply. [latex] \left( 4{{x}^{2}}+\sqrt[3]{x} \right)\left( \sqrt[3]{{{x}^{2}}}+2 \right)[/latex]
In the following video we show more examples of how to multiply two binomials that contain radicals.
(9.4.4) – Rationalize Denominators
Although radicals follow the same rules that integers do, it is often difficult to figure out the value of an expression containing radicals. For example, you probably have a good sense of how much [latex]\displaystyle \frac{4}{8},\ 0.75[/latex] and [latex]\displaystyle \frac{6}{9}[/latex] are, but what about the quantities [latex]\displaystyle \frac{1}{\sqrt{2}}[/latex] and [latex]\displaystyle \frac{1}{\sqrt{5}}[/latex]? These are much harder to visualize.
That said, sometimes you have to work with expressions that contain many radicals. Often the value of these expressions is not immediately clear. In cases where you have a fraction with a radical in the denominator, you can use a technique called rationalizing a denominator to eliminate the radical. The point of rationalizing a denominator is to make it easier to understand what the quantity really is by removing radicals from the denominators.
The idea of rationalizing a denominator makes a bit more sense if you consider the definition of “rationalize.” Recall that the numbers 5, [latex]\displaystyle \frac{1}{2}[/latex], and [latex] 0.75[/latex] are all known as rational numbers—they can each be expressed as a ratio of two integers ([latex]\displaystyle \frac{5}{1},\frac{1}{2}[/latex], and [latex]\displaystyle \frac{3}{4}[/latex] respectively). Some radicals are irrational numbers because they cannot be represented as a ratio of two integers. As a result, the point of rationalizing a denominator is to change the expression so that the denominator becomes a rational number.
Here are some examples of irrational and rational denominators.
|
Irrational |
Rational |
|
|---|---|---|
|
[latex]\displaystyle \frac{1}{\sqrt{2}}[/latex] |
= |
[latex]\displaystyle \frac{\sqrt{2}}{2}[/latex] |
|
[latex]\displaystyle \frac{2+\sqrt{3}}{\sqrt{3}}[/latex] |
= |
[latex]\displaystyle \frac{2\sqrt{3}+3}{3}[/latex] |
Now let’s examine how to get from irrational to rational denominators.
Rationalizing Denominators with One Term
Let’s start with the fraction [latex]\displaystyle \frac{1}{\sqrt{2}}[/latex]. Its denominator is [latex] \sqrt{2}[/latex], an irrational number. This makes it difficult to figure out what the value of [latex]\displaystyle \frac{1}{\sqrt{2}}[/latex] is.
You can rename this fraction without changing its value, if you multiply it by 1. In this case, set 1 equal to [latex]\displaystyle \frac{\sqrt{2}}{\sqrt{2}}[/latex]. Watch what happens.
[latex]\displaystyle \frac{1}{\sqrt{2}}\cdot 1=\frac{1}{\sqrt{2}}\cdot \frac{\sqrt{2}}{\sqrt{2}}=\frac{\sqrt{2}}{\sqrt{2\cdot 2}}=\frac{\sqrt{2}}{\sqrt{4}}=\frac{\sqrt{2}}{2}[/latex]
The denominator of the new fraction is no longer a radical (notice, however, that the numerator is).
So why choose to multiply [latex]\displaystyle \frac{1}{\sqrt{2}}[/latex] by [latex]\displaystyle \frac{\sqrt{2}}{\sqrt{2}}[/latex]? You knew that the square root of a number times itself will be a whole number. In algebraic terms, this idea is represented by [latex] \sqrt{x}\cdot \sqrt{x}=x[/latex]. Look back to the denominators in the multiplication of [latex]\displaystyle \frac{1}{\sqrt{2}}\cdot 1[/latex]. Do you see where [latex] \sqrt{2}\cdot \sqrt{2}=\sqrt{4}=2[/latex]?
In the following videos we show examples of rationalizing the denominator of a radical expression that contains integer radicands.
Here are some more examples. Notice how the value of the fraction is not changed at all—it is simply being multiplied by another name for 1.
Example
Rationalize the denominator.
[latex]\displaystyle \frac{2+\sqrt{3}}{\sqrt{3}}[/latex]
You can use the same method to rationalize denominators to simplify fractions with radicals that contain a variable. As long as you multiply the original expression by another name for 1, you can eliminate a radical in the denominator without changing the value of the expression itself.
Example
Rationalize the denominator.
[latex]\displaystyle \frac{\sqrt{x}+\sqrt{y}}{\sqrt{x}},\text{ where }x\ne \text{0}[/latex]
Example
Rationalize the denominator and simplify.
[latex]\displaystyle \sqrt{\frac{100x}{11y}},\text{ where }y\ne \text{0}[/latex]
Rationalizing the Denominator with Higher Roots
When we rationalized a square root, we multiplied the numerator and denominator by a square root that would give us a perfect square under the radical in the denominator. When we took the square root, the denominator no longer had a radical.
We will follow a similar process to rationalize higher roots. To rationalize a denominator with a higher index radical, we multiply the numerator and denominator by a radical that would give us a radicand that is a perfect power of the index. When we simplify the new radical, the denominator will no longer have a radical.
For example,
ExAMPLE
Rationalize the denominator and simplify. [latex]\displaystyle \frac{1}{\sqrt[3]{6}}[/latex]
ExAMPLE
Rationalize the denominator and simplify. [latex]\displaystyle \frac{3}{\sqrt[3]{4x}}[/latex]
Try It
Rationalizing Denominators with Two Terms
Denominators do not always contain just one term, as shown in the previous examples. Sometimes, you will see expressions like [latex]\displaystyle \frac{3}{\sqrt{2}+3}[/latex] where the denominator is composed of two terms, [latex] \sqrt{2}[/latex] and [latex]+3[/latex].
Unfortunately, you cannot rationalize these denominators the same way you rationalize single-term denominators. If you multiply [latex] \sqrt{2}+3[/latex] by [latex] \sqrt{2}[/latex], you get [latex] 2+3\sqrt{2}[/latex]. The original [latex] \sqrt{2}[/latex] is gone, but now the quantity [latex] 3\sqrt{2}[/latex] has appeared…this is no better!
In order to rationalize this denominator, you want to square the radical term and somehow prevent the integer term from being multiplied by a radical. Is this possible?
It is possible—and you have already seen how to do it!
Recall that when binomials of the form [latex] (a+b)(a-b)[/latex] are multiplied, the product is [latex] [/latex]. So, for example, [latex] (x+3)(x-3)={{x}^{2}}-3x+3x-9={{x}^{2}}-9[/latex]; notice that the terms [latex]−3x[/latex] and [latex]+3x[/latex] combine to 0. Now for the connection to rationalizing denominators: what if you replaced x with [latex] \sqrt{2}[/latex]?
Look at the side by side examples below. Just as [latex] -3x+3x[/latex] combines to 0 on the left, [latex] -3\sqrt{2}+3\sqrt{2}[/latex] combines to 0 on the right.
| [latex](x+3)(x-3)[/latex] | [latex]\left( \sqrt{2}+3 \right)\left( \sqrt{2}-3 \right)[/latex] |
| [latex]={{x}^{2}}-3x+3x-9[/latex] | [latex]={{\left( \sqrt{2} \right)}^{2}}-3\sqrt{2}+3\sqrt{2}-9[/latex] |
| [latex]={{x}^{2}}-9[/latex] | [latex]={{\left( \sqrt{2} \right)}^{2}}-9[/latex] |
| [latex]=2-9[/latex] | |
| [latex]-7[/latex] |
There you have it! Multiplying [latex] \sqrt{2}+3[/latex] by [latex] \sqrt{2}-3[/latex] removed one radical without adding another.
In this example, [latex] \sqrt{2}-3[/latex] is known as a conjugate, and [latex] \sqrt{2}+3[/latex] and [latex] \sqrt{2}-3[/latex] are known as a conjugate pair. To find the conjugate of a binomial that includes radicals, change the sign of the second term to its opposite as shown in the table below.
| Term | Conjugate | Product |
|---|---|---|
| [latex] \sqrt{2}+3[/latex] | [latex] \sqrt{2}-3[/latex] | [latex] \left( \sqrt{2}+3 \right)\left( \sqrt{2}-3 \right)={{\left( \sqrt{2} \right)}^{2}}-{{\left( 3 \right)}^{2}}=2-9=-7[/latex] |
| [latex] \sqrt{x}-5[/latex] | [latex] \sqrt{x}+5[/latex] | [latex] \left( \sqrt{x}-5 \right)\left( \sqrt{x}+5 \right)={{\left( \sqrt{x} \right)}^{2}}-{{\left( 5 \right)}^{2}}=x-25[/latex] |
| [latex] 8-2\sqrt{x}[/latex] | [latex] 8+2\sqrt{x}[/latex] | [latex] \left( 8-2\sqrt{x} \right)\left( 8+2\sqrt{x} \right)={{\left( 8 \right)}^{2}}-{{\left( 2\sqrt{x} \right)}^{2}}=64-4x[/latex] |
| [latex] 1+\sqrt{xy}[/latex] | [latex] 1-\sqrt{xy}[/latex] | [latex] \left( 1+\sqrt{xy} \right)\left( 1-\sqrt{xy} \right)={{\left( 1 \right)}^{2}}-{{\left( \sqrt{xy} \right)}^{2}}=1-xy[/latex] |
Example
Rationalize the denominator and simplify.
[latex]\displaystyle \frac{5-\sqrt{7}}{3+\sqrt{5}}[/latex]
Example
Rationalize the denominator and simplify. [latex]\displaystyle \frac{\sqrt{x}}{\sqrt{x}+2}[/latex]
One word of caution: this method will work for binomials that include a square root, but not for binomials with roots greater than 2. This is because squaring a root that has an index greater than 2 does not remove the root, as shown below.
[latex] \begin{array}{l}\left( \sqrt[3]{10}+5 \right)\left( \sqrt[3]{10}-5 \right)\\={{\left( \sqrt[3]{10} \right)}^{2}}-5\sqrt[3]{10}+5\sqrt[3]{10}-25\\={{\left( \sqrt[3]{10} \right)}^{2}}-25\\=\sqrt[3]{100}-25\end{array}[/latex]
[latex] \sqrt[3]{100}[/latex] cannot be simplified any further, since its prime factors are [latex] 2\cdot 2\cdot 5\cdot 5[/latex]. There are no cubed numbers to pull out! Multiplying [latex] \sqrt[3]{10}+5[/latex] by its conjugate does not result in a radical-free expression.
In the following video we show more examples of how to rationalize a denominator using the conjugate.
