9.3 – Radical Functions

Learning Objectives

  • (9.3.1) – Evaluating Radical functions
  • (9.3.2) – Finding the domain of a radical function

In this section we will extend our previous work with functions to include radicals. If a function is defined by a radical expression, we call it a radical function.

The square root function is [latex]f(x) = \sqrt{x}[/latex].

The cube root function is [latex]f(x) = \sqrt[3]{x}[/latex].

A radical function is a function that is defined by a radical expression.

The following are examples of rational functions: [latex]f(x)=\sqrt{2x^4-5}[/latex]; [latex]g(x)=\sqrt[3]{4x-7}[/latex]; [latex]h(x)=\sqrt[7]{-8x^2+4}[/latex].

(9.3.1) – Evaluating a radical function

To evaluate a radical function, we find the value of [latex]f(x)[/latex] for a given value of [latex]x[/latex] just as we did in our previous work with functions.

EXAMPLE

For the function [latex]f(x) = \sqrt{2x-1}[/latex], find [latex]f(5)[/latex]

EXAMPLE

For the function [latex]f(x) = \sqrt{-4x+5}[/latex], find [latex]f(-5)[/latex]

 

Try It

In the following example we evaluate a cube root function.

ExAMPLE

For the function [latex]f(x) = \sqrt[3]{x-29}[/latex], find [latex]f(2)[/latex]

(9.3.2) – Finding the domain of a radical function

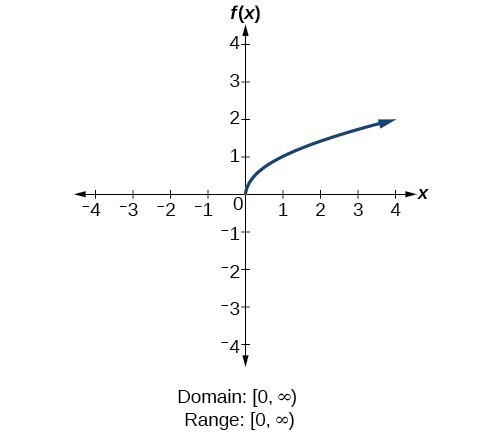
For the square root function [latex]f\left(x\right)=\sqrt[]{x}[/latex], we cannot take the square root of a negative real number, so the domain must be 0 or greater. The range also excludes negative numbers because the square root of a positive number [latex]x[/latex] is defined to be positive, even though the square of the negative number [latex]-\sqrt{x}[/latex] also gives us [latex]x[/latex]. The following is a graph of the square root function:

Square root function f(x)=sqrt(x).

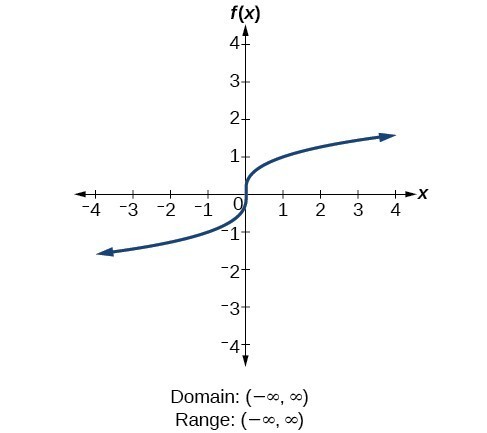
For the cube root function [latex]f\left(x\right)=\sqrt[3]{x}[/latex], the domain and range include all real numbers. Note that there is no problem taking a cube root, or any odd-integer root, of a negative number, and the resulting output is negative (it is an odd function). Here is the graph of the cube root function:

Cube root function f(x)=x^(1/3).

We use this to find the domains of other radical functions.

How To: Given a function written in equation form including an even root, find the domain.

  1. Identify the input values.
  2. Since there is an even root, exclude any real numbers that result in a negative number in the radicand. Set the radicand greater than or equal to zero and solve for [latex]x[/latex].
  3. The solution(s) are the domain of the function. If possible, write the answer in interval form.

Example: Finding the Domain of a Function with an Even Root

Find the domain of the function [latex]f\left(x\right)=\sqrt{7-x}[/latex].

EXAMPLE

Find the domain of the function [latex]f\left(x\right)=\sqrt{5+2x}[/latex].

Try It

Example: Finding the Domain and Range

Find the domain and range of [latex]f\left(x\right)=2\sqrt{x+4}[/latex].