Learning Objectives

(9.2.1) – Define and identify a radical expression
(9.2.2) – Convert radicals to expressions with rational exponents
(9.2.3) – Convert expressions with rational exponents to their radical equivalent
(9.2.4) – Rational exponents whose numerator is not equal to one
(9.2.5) – Simplify Radical Expressions
- Simplify radical expressions using factoring
- Simplify radical expressions using rational exponents and the laws of exponents

(9.2.1) – Define and identify a radical expression

Square roots are most often written using a radical sign, like this, $\sqrt{4}$ . But there is another way to represent them. You can use rational exponents instead of a radical. A rational exponent is an exponent that is a fraction. For example, $\sqrt{4}$ can be written as ${{4}^{\tfrac{1}{2}}}$ .

Can’t imagine raising a number to a rational exponent? They may be hard to get used to, but rational exponents can actually help simplify some problems. Writing radicals with rational exponents will come in handy when we discuss techniques for simplifying more complex radical expressions.

Radical expressions are expressions that contain radicals. Radical expressions come in many forms, from simple and familiar, such as $\sqrt{16}$ , to quite complicated, as in $\sqrt[3]{250{{x}^{4}}y}$

(9.2.2) – Convert radicals to expressions with rational exponents

Radicals and fractional exponents are alternate ways of expressing the same thing. In the table below we show equivalent ways to express radicals: with a root, with a rational exponent, and as a principal root.

Radical Form	Exponent Form	Principal Root
$\sqrt{16}$	${{16}^{\tfrac{1}{2}}}$	4
$\sqrt{25}$	${{25}^{\tfrac{1}{2}}}$	5
$\sqrt{100}$	${{100}^{\tfrac{1}{2}}}$	10

Let’s look at some more examples, but this time with cube roots. Remember, cubing a number raises it to the power of three. Notice that in the examples in the table below, the denominator of the rational exponent is the number 3.

Radical Form	Exponent Form	Principal Root
$\sqrt[3]{8}$	${{8}^{\tfrac{1}{3}}}$	2
$\sqrt[3]{8}$	${{125}^{\tfrac{1}{3}}}$	5
$\sqrt[3]{1000}$	${{1000}^{\tfrac{1}{3}}}$	10

These examples help us model a relationship between radicals and rational exponents: namely, that the $n^{th}$ root of a number can be written as either $\sqrt[n]{x}$ or ${{x}^{\frac{1}{n}}}$ .

Radical Form	Exponent Form
$\sqrt{x}$	${{x}^{\tfrac{1}{2}}}$
$\sqrt[3]{x}$	${{x}^{\tfrac{1}{3}}}$
$\sqrt[4]{x}$	${{x}^{\tfrac{1}{4}}}$
…	…
$\sqrt[n]{x}$	${{x}^{\tfrac{1}{n}}}$

In the table above, notice how the denominator of the rational exponent determines the index of the root. So, an exponent of $\frac{1}{2}$ translates to the square root, an exponent of $\frac{1}{5}$ translates to the fifth root or ${\,}^5\hspace{-0.1in} \sqrt{\,\,\,}$ , and $\frac{1}{8}$ translates to the eighth root or ${\,}^8\hspace{-0.1in} \sqrt{\,\,\,}$ .

Example

Express ${{(2x)}^{^{\frac{1}{3}}}}$ in radical form.

Show Solution

Rewrite the expression with the fractional exponent as a radical. The denominator of the fraction determines the root, in this case the cube root.

$\sqrt[3]{2x}$

The parentheses in ${{\left( 2x \right)}^{\frac{1}{3}}}$ indicate that the exponent refers to everything within the parentheses.

Answer

${{(2x)}^{^{\frac{1}{3}}}}=\sqrt[3]{2x}$

Remember that exponents only refer to the quantity immediately to their left unless a grouping symbol is used. The example below looks very similar to the previous example with one important difference—there are no parentheses! Look what happens.

Example

Express $2{{x}^{^{\frac{1}{3}}}}$ in radical form.

Show Solution

Rewrite the expression with the fractional exponent as a radical. The denominator of the fraction determines the root, in this case the cube root.

$2\sqrt[3]{x}$

The exponent refers only to the part of the expression immediately to the left of the exponent, in this case x, but not the 2.

Answer

$2{{x}^{^{\frac{1}{3}}}}=2\sqrt[3]{x}$

(9.2.3) – Convert expressions with rational exponents to their radical equivalent

Person sitting on the ground with one leg arched behind them and one leg curved in front of them.

Flexibility

We can write radicals with rational exponents, and as we will see when we simplify more complex radical expressions, this can make things easier. Having different ways to express and write algebraic expressions allows us to have flexibility in solving and simplifying them. It is like having a thesaurus when you write, you want to have options for expressing yourself!

Example

Write $\sqrt[4]{81}$ as an expression with a rational exponent.

Show Solution

The radical form

^{4} \sqrt{}

${\,}^4\hspace{-0.1in}\sqrt{{\,\,\,\,}}$ can be rewritten as the exponent

\frac{1}{4}

$\frac{1}{4}$ . Remove the radical and place the exponent next to the base.

${{81}^{\frac{1}{4}}}$

Answer

$\sqrt[4]{81}={{81}^{\frac{1}{4}}}$

Example

Express $4\sqrt[3]{xy}$ with rational exponents.

Show Solution

Rewrite the radical using a rational exponent. The root determines the fraction. In this case, the index of the radical is 3, so the rational exponent will be

\frac{1}{3}

$\frac{1}{3}$ .

$4{{(xy)}^{\frac{1}{3}}}$

Since 4 is outside the radical, it is not included in the grouping symbol and the exponent does not refer to it.

Answer

$4\sqrt[3]{xy}=4{{(xy)}^{\frac{1}{3}}}$

(9.2.4) – Rational exponents whose numerator is not equal to one

All of the numerators for the fractional exponents in the examples above were 1. You can use fractional exponents that have numerators other than 1 to express roots, as shown below.

Radical	Exponent
$\sqrt{9}$	$9^{\frac{1}{2}}$
$\sqrt[3]{{{9}^{2}}}$	$9^{\frac{2}{3}}$
$\sqrt[4]{9^{3}}$	$9^{\frac{3}{4}}$
$\sqrt[5]{9^{2}}$	$9^{\frac{2}{5}}$
…	…
$\sqrt[n]{9^{x}}$	$9\frac{x}{n}$

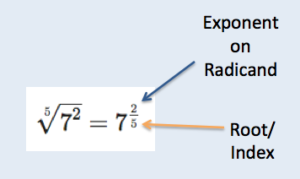
Screen Shot 2016-07-29 at 3.56.45 PM

To rewrite a radical using a fractional exponent, the power to which the radicand is raised becomes the numerator and the root/ index becomes the denominator.

Writing Rational Exponents

Any radical in the form $\large \sqrt[n]{a^{m}}$ can be written using a fractional exponent in the form $\large a^{\frac{m}{n}}$ .

The relationship between $\sqrt[n]{{{a}^{m}}}$ and ${{a}^{\frac{m}{n}}}$ works for rational exponents that have a numerator of 1 as well. For example, the radical $\sqrt[3]{8}$ can also be written as $\sqrt[3]{{{8}^{1}}}$ , since any number remains the same value if it is raised to the first power. You can now see where the numerator of 1 comes from in the equivalent form of ${{8}^{\frac{1}{3}}}$ .

In the next example, we practice writing radicals with rational exponents where the numerator is not equal to one.

Example

Rewrite the radicals using a rational exponent, then simplify your result.

$\sqrt[3]{{{a}^{6}}}$
$\sqrt[12]{16^3}$

Show Solution

1. $\sqrt[n]{a^{m}}$ can be rewritten as $a^{\frac{m}{n}}$ , so in this case $n=3,\text{ and }m=6$ , therefore

$\sqrt[3]{{{a}^{6}}}={{a}^{\frac{6}{3}}}$

Simplify the exponent.

${{a}^{\frac{6}{3}}}={{a}^{2}}$

Answer

$\sqrt[3]{{{a}^{6}}}={{a}^{2}}$

2. $\sqrt[n]{a^{m}}$ can be rewritten as $a^{\frac{m}{n}}$ , so in this case $n=12,\text{ and }m=3$ , therefore

$\sqrt[12]{16^3}={16}^{\frac{3}{12}}={16}^{\frac{1}{4}}$

Simplify the expression using rules for exponents.

$\begin{array}{ccc}16=2^4\\{16}^{\frac{1}{4}}={2^4}^{\frac{1}{4}}\\=2^{4\cdot\frac{1}{4}}\\=2^1=2\end{array}$

Answer

$\sqrt[12]{16^3}=2$

In our last example we will rewrite expressions with rational exponents as radicals. This practice will help us when we simplify more complicated radical expressions, and as we learn how to solve radical equations. Typically it is easier to simplify when we use rational exponents, but this exercise is intended to help you understand how the numerator and denominator of the exponent are the exponent of a radicand and index of a radical.

Example

Rewrite the expressions using a radical.

${x}^{\frac{2}{3}}$
${5}^{\frac{4}{7}}$

Show Answer

${x}^{\frac{2}{3}}$ , the numerator is 2 and the denominator is 3, therefore we will have the third root of x squared, $\sqrt[3]{x^2}$
${5}^{\frac{4}{7}}$ , the numerator is 4 and the denominator is 7, so we will have the seventh root of 5 raised to the fourth power. $\sqrt[7]{5^4}$

In the following video we show more examples of writing radical expressions with rational exponents and expressions with rational exponents as radical expressions.

We will use this notation later, so come back for practice if you forget how to write a radical with a rational exponent.

(9.2.5) – Simplify Radical Expressions

To simplify complicated radical expressions, we can use some definitions and rules from simplifying exponents. Recall the Product Raised to a Power Rule from when you studied exponents. This rule states that the product of two or more non-zero numbers raised to a power is equal to the product of each number raised to the same power. In math terms, it is written $\left(ab\right)^{x}=a^{x}\cdot{b}^{x}$ . So, for example, you can use the rule to rewrite ${{\left( 3x \right)}^{2}}$ as ${{3}^{2}}\cdot {{x}^{2}}=9\cdot {{x}^{2}}=9{{x}^{2}}$ .

Now instead of using the exponent 2, let’s use the exponent $\frac{1}{2}$ . The exponent is distributed in the same way.

${{\left( 3x \right)}^{\frac{1}{2}}}={{3}^{\frac{1}{2}}}\cdot {{x}^{\frac{1}{2}}}$

And since you know that raising a number to the $\frac{1}{2}$ power is the same as taking the square root of that number, you can also write it this way.

$\sqrt{3x}=\sqrt{3}\cdot \sqrt{x}$

Look at that—you can think of any number underneath a radical as the product of separate factors, each underneath its own radical.

A Product Raised to a Power Rule or sometimes called The Square Root of a Product Rule

For any real numbers $a$ and $b$ , $\sqrt{ab}=\sqrt{a}\cdot \sqrt{b}$ .

For example: $\sqrt{100}=\sqrt{10}\cdot \sqrt{10}$ , and $\sqrt{75}=\sqrt{25}\cdot \sqrt{3}$

This rule is important because it helps you think of one radical as the product of multiple radicals. If you can identify perfect squares within a radical, as with $\sqrt{(2\cdot 2)(2\cdot 2)(3\cdot 3})$ , you can rewrite the expression as the product of multiple perfect squares: $\sqrt{{{2}^{2}}}\cdot \sqrt{{{2}^{2}}}\cdot \sqrt{{{3}^{2}}}$ .

The square root of a product rule will help us simplify roots that aren’t perfect, as is shown the following example.

Simplify radical expressions using factoring

Example

Simplify. $\sqrt{63}$

Show Solution

63 is not a perfect square so we can use the square root of a product rule to simplify any factors that are perfect squares.
Factor 63 into 7 and 9.

$\sqrt{7\cdot 9}$

9 is a perfect square, $9=3^2$ , therefore we can rewrite the radicand.

$\sqrt{7\cdot {{3}^{2}}}$

Using the Product Raised to a Power rule, separate the radical into the product of two factors, each under a radical.

$\sqrt{7}\cdot \sqrt{{{3}^{2}}}$

Take the square root of $3^{2}$ .

$\sqrt{7}\cdot 3$

Rearrange factors so the integer appears before the radical, and then multiply. (This is done so that it is clear that only the 7 is under the radical, not the 3.)

$3\cdot \sqrt{7}$

Answer
$\sqrt{63}=3\sqrt{7}$

The final answer $3\sqrt{7}$ may look a bit odd, but it is in simplified form. You can read this as “three radical seven” or “three times the square root of seven.”

The following video shows more examples of how to simplify square roots that do not have perfect square radicands.

Before we move on to simplifying more complex radicals with variables, we need to learn about an important behavior of square roots with variables in the radicand.

Consider the expression $\sqrt{{{x}^{2}}}$ . This looks like it should be equal to x, right? Let’s test some values for x and see what happens.

In the chart below, look along each row and determine whether the value of x is the same as the value of $\sqrt{{{x}^{2}}}$ . Where are they equal? Where are they not equal?

After doing that for each row, look again and determine whether the value of $\sqrt{{{x}^{2}}}$ is the same as the value of $\left|x\right|$ .

$x$	$x^{2}$	$\sqrt{x^{2}}$	$\left\|x\right\|$
$−5$	25	5	5
$−2$	4	2	2
0	0	0	0
6	36	6	6
10	100	10	10

Notice—in cases where x is a negative number, $\sqrt{x^{2}}\neq{x}$ ! However, in all cases $\sqrt{x^{2}}=\left|x\right|$ . You need to consider this fact when simplifying radicals with an even index that contain variables, because by definition $\sqrt{x^{2}}$ is always nonnegative.

Taking the Square Root of a Radical Expression

When finding the square root of an expression that contains variables raised to a power, consider that $\sqrt{x^{2}}=\left|x\right|$ .

Examples: $\sqrt{9x^{2}}=3\left|x\right|$ , and $\sqrt{16{{x}^{2}}{{y}^{2}}}=4\left|xy\right|$

We will combine this with the square root of a product rule in our next example to simplify an expression with three variables in the radicand.

Example

Simplify. $\sqrt{{{a}^{3}}{{b}^{5}}{{c}^{2}}}$

Show Solution

Factor to find variables with even exponents.

$\sqrt{{{a}^{2}}\cdot a\cdot {{b}^{4}}\cdot b\cdot {{c}^{2}}}$

Rewrite $b^{4}$ as $\left(b^{2}\right)^{2}$ .

$\sqrt{{{a}^{2}}\cdot a\cdot {{({{b}^{2}})}^{2}}\cdot b\cdot {{c}^{2}}}$

Separate the squared factors into individual radicals.

$\sqrt{{{a}^{2}}}\cdot \sqrt{{{({{b}^{2}})}^{2}}}\cdot \sqrt{{{c}^{2}}}\cdot \sqrt{a\cdot b}$

Take the square root of each radical. Remember that $\sqrt{{{a}^{2}}}=\left| a \right|$ .

$\left| a \right|\cdot {{b}^{2}}\cdot \left|{c}\right|\cdot \sqrt{a\cdot b}$

Simplify and multiply.

$\left| ac \right|{{b}^{2}}\sqrt{ab}$

Answer

$\sqrt{{{a}^{3}}{{b}^{5}}{{c}^{2}}}=\left| ac \right|{{b}^{2}}\sqrt{ab}$

Analysis of the Solution

Why didn’t we write $b^2$ as $|b^2|$ ? Because when you square a number, you will always get a positive result, so the principal square root of $\left(b^2\right)^2$ will always be non-negative. One tip for knowing when to apply the absolute value after simplifying any even indexed root is to look at the final exponent on your variable terms. If the exponent is odd – including 1 – add an absolute value. This applies to simplifying any root with an even index, as we will see in later examples.

In the following video you will see more examples of how to simplify radical expressions with variables.

We will show another example where the simplified expression contains variables with both odd and even powers.

Example

Simplify. $\sqrt{9{{x}^{6}}{{y}^{4}}}$

Show Solution

Factor to find identical pairs.

$\sqrt{3\cdot 3\cdot {{x}^{3}}\cdot {{x}^{3}}\cdot {{y}^{2}}\cdot {{y}^{2}}}$

Rewrite the pairs as perfect squares.

$\sqrt{{{3}^{2}}\cdot {{\left( {{x}^{3}} \right)}^{2}}\cdot {{\left( {{y}^{2}} \right)}^{2}}}$

Separate into individual radicals.

$\sqrt{{{3}^{2}}}\cdot \sqrt{{{\left( {{x}^{3}} \right)}^{2}}}\cdot \sqrt{{{\left( {{y}^{2}} \right)}^{2}}}$

Simplify.

$3{{x}^{3}}{{y}^{2}}$

Because x has an odd power, we will add the absolute value for our final solution.

$3|{{x}^{3}}|{{y}^{2}}$

Answer

$\sqrt{9{{x}^{6}}{{y}^{4}}}=3|{{x}^{3}}|{y}$

ExAMPLE

Simplify $\sqrt{x^2-6x+9}$ .

Show Answer

First, we factor the radicand:

$x^2-6x+9 = (x-3)^2$

Then, we rewrite the radical expression and take the square root:

$\sqrt{x^2-6x+9}=\sqrt{(x-3)^2} = |x-3|$

Answer

$|x-3|$

Analysis of the solution:

Note, that if we didn’t include the absolute value signs, the two sides of the equation would be different for values of $x$ less than 3. For example, evaluating the radical expression at $x=1$ would give us $\sqrt{(1-3)^2}=\sqrt{(-2)^2}=2$ ; and plugging in $x=1$ into our final answer, also yields: $|1-3|=2$ . However, if we did not put absolute value signs, plugging in $x=1$ into $x-3$ would yield $1-3=-2$ , a different value.

In our next example we will start with an expression written with a rational exponent. You will see that you can use a similar process – factoring and sorting terms into squares – to simplify this expression.

Example

Simplify. ${{(36{{x}^{4}})}^{\frac{1}{2}}}$

Show Solution

Rewrite the expression with the fractional exponent as a radical.

$\sqrt{36{{x}^{4}}}$

Find the square root of both the coefficient and the variable.

$\begin{array}{c}\sqrt{{{6}^{2}}\cdot {{x}^{4}}} &=&\sqrt{{{6}^{2}}}\cdot \sqrt{{{x}^{4}}}\\ &=&\sqrt{{{6}^{2}}}\cdot \sqrt{{{({{x}^{2}})}^{2}}}\\ &=&6\cdot{x}^{2}\end{array}$

Answer

${{(36{{x}^{4}})}^{\frac{1}{2}}}=6{{x}^{2}}$

Here is one more example with perfect squares.

Example

Simplify. $\sqrt{49{{x}^{10}}{{y}^{8}}}$

Show Solution

Look for squared numbers and variables. Factor 49 into

7 \cdot 7

$7\cdot7$ ,

x^{10}

$x^{10}$ into

x^{5} \cdot x^{5}

$x^{5}\cdot{x}^{5}$ , and

y^{8}

$y^{8}$ into

y^{4} \cdot y^{4}

$y^{4}\cdot{y}^{4}$ .

$\sqrt{7\cdot 7\cdot {{x}^{5}}\cdot {{x}^{5}}\cdot {{y}^{4}}\cdot {{y}^{4}}}$

Rewrite the pairs as squares.

$\sqrt{{{7}^{2}}\cdot {{({{x}^{5}})}^{2}}\cdot {{({{y}^{4}})}^{2}}}$

Separate the squared factors into individual radicals.

$\sqrt{{{7}^{2}}}\cdot \sqrt{{{({{x}^{5}})}^{2}}}\cdot \sqrt{{{({{y}^{4}})}^{2}}}$

Take the square root of each radical using the rule that $\sqrt{{{x}^{2}}}=x$ .

$7\cdot {{x}^{5}}\cdot {{y}^{4}}$

Multiply.

$7{{x}^{5}}{{y}^{4}}$

Answer

$\sqrt{49{{x}^{10}}{{y}^{8}}}=7|{{x}^{5}}|{{y}^{4}}$

Simplify cube roots

We can use the same techniques we have used for simplifying square roots to simplify higher order roots. For example to simplify a cube root, the goal is to find factors under the radical that are perfect cubes so that you can take their cube root. We no longer need to be concerned about whether we have identified the principal root since we are now finding cube roots. Focus on finding identical trios of factors as you simplify.

Example

Simplify. $\sqrt[3]{40{{m}^{5}}}$

Show Solution

Factor 40 into prime factors.

$\sqrt[3]{5\cdot 2\cdot 2\cdot 2\cdot {{m}^{5}}}$

Since you are looking for the cube root, you need to find factors that appear 3 times under the radical. Rewrite $2\cdot 2\cdot 2$ as ${{2}^{3}}$ .

$\sqrt[3]{{{2}^{3}}\cdot 5\cdot {{m}^{5}}}$

Rewrite ${{m}^{5}}$ as ${{m}^{3}}\cdot {{m}^{2}}$ .

$\sqrt[3]{{{2}^{3}}\cdot 5\cdot {{m}^{3}}\cdot {{m}^{2}}}$

Rewrite the expression as a product of multiple radicals.

$\sqrt[3]{{{2}^{3}}}\cdot \sqrt[3]{5}\cdot \sqrt[3]{{{m}^{3}}}\cdot \sqrt[3]{{{m}^{2}}}$

Simplify and multiply.

$2\cdot \sqrt[3]{5}\cdot m\cdot \sqrt[3]{{{m}^{2}}}$

Answer

$\sqrt[3]{40{{m}^{5}}}=2m\sqrt[3]{5{{m}^{2}}}$

Remember that you can take the cube root of a negative expression. In the next example we will simplify a cube root with a negative radicand.

Example

Simplify. $\sqrt[3]{-27{{x}^{4}}{{y}^{3}}}$

Show Solution

Factor the expression into cubes.

Separate the cubed factors into individual radicals.

$\begin{array}{r}\sqrt[3]{-1\cdot 27\cdot {{x}^{4}}\cdot {{y}^{3}}} &=& \sqrt[3]{{{(-1)}^{3}}\cdot {{(3)}^{3}}\cdot {{x}^{3}}\cdot x\cdot {{y}^{3}}}\\ &=& \sqrt[3]{{{(-1)}^{3}}}\cdot \sqrt[3]{{{(3)}^{3}}}\cdot \sqrt[3]{{{x}^{3}}}\cdot \sqrt[3]{x}\cdot \sqrt[3]{{{y}^{3}}}\end{array}$

Simplify the cube roots.

$-1\cdot 3\cdot x\cdot y\cdot \sqrt[3]{x}$

Answer

$\sqrt[3]{-27{{x}^{4}}{{y}^{3}}}=-3xy\sqrt[3]{x}$

Analysis of the solution

You could check your answer by performing the inverse operation. If you are right, when you cube $-3xy\sqrt[3]{x}$ you should get $-27{{x}^{4}}{{y}^{3}}$ .

$\begin{array}{l}\left( -3xy\sqrt[3]{x} \right)\left( -3xy\sqrt[3]{x} \right)\left( -3xy\sqrt[3]{x} \right) &=& -3\cdot -3\cdot -3\cdot x\cdot x\cdot x\cdot y\cdot y\cdot y\cdot \sqrt[3]{x}\cdot \sqrt[3]{x}\cdot \sqrt[3]{x}\\ &=& -27\cdot {{x}^{3}}\cdot {{y}^{3}}\cdot \sqrt[3]{{{x}^{3}}}\\ &=& -27{{x}^{3}}{{y}^{3}}\cdot x\\ &=& -27{{x}^{4}}{{y}^{3}}\end{array}$

You can also skip the step of factoring out the negative one once you are comfortable with identifying cubes.

Example

Simplify. $\sqrt[3]{-24{{a}^{5}}}$

Show Solution

Factor

$−24$ to find perfect cubes. Here,

$−1$ and 8 are the perfect cubes.

$\sqrt[3]{-1\cdot 8\cdot 3\cdot {{a}^{5}}}$

Factor variables. You are looking for cube exponents, so you factor $a^{5}$ into $a^{3}$ and $a^{2}$ .

$\sqrt[3]{{{(-1)}^{3}}\cdot {{2}^{3}}\cdot 3\cdot {{a}^{3}}\cdot {{a}^{2}}}$

Separate the factors into individual radicals.

$\sqrt[3]{{{(-1)}^{3}}}\cdot \sqrt[3]{{{2}^{3}}}\cdot \sqrt[3]{{{a}^{3}}}\cdot \sqrt[3]{3\cdot {{a}^{2}}}$

Simplify, using the property $\sqrt[3]{{{x}^{3}}}=x$ .

$-1\cdot 2\cdot a\cdot \sqrt[3]{3\cdot {{a}^{2}}}$

This is the simplest form of this expression; all cubes have been pulled out of the radical expression.

$-2a\sqrt[3]{3{{a}^{2}}}$

Answer

$\sqrt[3]{-24{{a}^{5}}}=-2a\sqrt[3]{3{{a}^{2}}}$

Analysis of the solution

You can check your answer by squaring it to be sure it equals $100{{x}^{2}}{{y}^{4}}$ .

In the following video we show more examples of simlifying cube roots.

Simplifying fourth roots

Now let’s move to simplifying fourth degree roots. No matter what root you are simplifying, the same idea applies, find cubes for cube roots, powers of four for fourth roots, etc. Recall that when your simplified expression contains an even indexed radical and a variable factor with an odd exponent, you need to apply an absolute value.

Example

Simplify. $\sqrt[4]{81{{x}^{8}}{{y}^{3}}}$

Show Solution

Rewrite the expression.

$\sqrt[4]{81}\cdot \sqrt[4]{{{x}^{8}}}\cdot \sqrt[4]{{{y}^{3}}}$

Factor each radicand.

$\sqrt[4]{3\cdot 3\cdot 3\cdot 3}\cdot \sqrt[4]{{{x}^{2}}\cdot {{x}^{2}}\cdot {{x}^{2}}\cdot {{x}^{2}}}\cdot \sqrt[4]{{{y}^{3}}}$

Simplify.

$\sqrt[4]{{{3}^{4}}}\cdot \sqrt[4]{{{({{x}^{2}})}^{4}}}\cdot \sqrt[4]{{{y}^{3}}} =3\cdot {{x}^{2}}\cdot \sqrt[4]{{{y}^{3}}}$

Answer

$\sqrt[4]{81x^{8}y^{3}}=3x^{2}\sqrt[4]{y^{3}}$

Simplify radical expressions using rational exponents and the laws of exponents

An alternative method to factoring is to rewrite the expression with rational exponents, then use the rules of exponents to simplify. You may find that you prefer one method over the other. Either way, it is nice to have options. We will show the last example again, using this idea.

Example

Simplify. $\sqrt[4]{81{{x}^{8}}{{y}^{3}}}$

Show Solution

Rewrite the radical using rational exponents.

${{(81{{x}^{8}}{{y}^{3}})}^{\frac{1}{4}}}$

Use the rules of exponents to simplify the expression.

$\begin{array}{r}{{81}^{\frac{1}{4}}}\cdot {{x}^{\frac{8}{4}}}\cdot {{y}^{\frac{3}{4}}}&=& {{(3\cdot 3\cdot 3\cdot 3)}^{\frac{1}{4}}}{{x}^{2}}{{y}^{\frac{3}{4}}}\\ &=& {{({{3}^{4}})}^{\frac{1}{4}}}{{x}^{2}}{{y}^{\frac{3}{4}}}\\ &=&3{{x}^{2}}{{y}^{\frac{3}{4}}}\end{array}$

Change the expression with the rational exponent back to radical form.

$3{{x}^{2}}\sqrt[4]{{{y}^{3}}}$

Answer

$\sqrt[4]{81{{x}^{8}}{{y}^{3}}}=3{{x}^{2}}\sqrt[4]{{{y}^{3}}}$

In the following video we show another example of how to simplify a fourth and fifth root.

For our last example, we will simplify a more complicated expression, $\large\frac{10{{b}^{2}}{{c}^{2}}}{c\sqrt[3]{8{{b}^{4}}}}$ . This expression has two variables, a fraction, and a radical. Let’s take it step-by-step and see if using fractional exponents can help us simplify it.
We will start by simplifying the denominator, since this is where the radical sign is located. Recall that an exponent in the denominator or a fraction can be rewritten as a negative exponent.

Example

Simplify. $\displaystyle \frac{10{{b}^{2}}{{c}^{2}}}{c\sqrt[3]{8{{b}^{4}}}}$

Show Solution

Separate the factors in the denominator.

$\displaystyle \frac{10{{b}^{2}}{{c}^{2}}}{c\cdot \sqrt[3]{8}\cdot \sqrt[3]{{{b}^{4}}}}$

Take the cube root of 8, which is 2.

$\displaystyle \frac{10{{b}^{2}}{{c}^{2}}}{c\cdot 2\cdot \sqrt[3]{{{b}^{4}}}}$

Rewrite the radical using a fractional exponent.

$\displaystyle \frac{10{{b}^{2}}{{c}^{2}}}{c\cdot 2\cdot {{b}^{\frac{4}{3}}}}$

Rewrite the fraction as a series of factors in order to cancel factors (see next step).

$\displaystyle \frac{10}{2}\cdot \frac{{{c}^{2}}}{c}\cdot \frac{{{b}^{2}}}{{{b}^{\frac{4}{3}}}}$

Simplify the constant and $c$ factors.

$\displaystyle 5\cdot c\cdot \frac{{{b}^{2}}}{{{b}^{\frac{4}{3}}}}$

Use the rule of negative exponents, $\displaystyle n^{-x} = \frac{1}{{{n}^{x}}}$ , to rewrite $\displaystyle \frac{1}{{{b}^{\tfrac{4}{3}}}}$ as $\displaystyle {{b}^{-\tfrac{4}{3}}}$ .

$\displaystyle 5c{{b}^{2}}{{b}^{-\ \frac{4}{3}}}$

Combine the $b$ factors by adding the exponents.

$\displaystyle 5c{{b}^{\frac{2}{3}}}$

Change the expression with the fractional exponent back to radical form. By convention, an expression is not usually considered simplified if it has a fractional exponent or a radical in the denominator.

$5c\sqrt[3]{{{b}^{2}}}$

Answer

$\displaystyle \frac{10{{b}^{2}}{{c}^{2}}}{c\sqrt[3]{8{{b}^{4}}}}=5c\sqrt[3]{{{b}^{2}}}$

Well, that took a while, but you did it. You applied what you know about fractional exponents, negative exponents, and the rules of exponents to simplify the expression.

In our last video we show how to use rational exponents to simplify radical expressions.

Summary

A radical expression is a mathematical way of representing the nth root of a number. Square roots and cube roots are the most common radicals, but a root can be any number. To simplify radical expressions, look for exponential factors within the radical, and then use the property $\sqrt[n]{{{x}^{n}}}=x$ if n is odd, and $\sqrt[n]{{{x}^{n}}}=\left| x \right|$ if n is even to pull out quantities. All rules of integer operations and exponents apply when simplifying radical expressions.

The steps to consider when simplifying a radical are outlined below.

Simplifying a radical

When working with exponents and radicals:

If n is odd, $\sqrt[n]{{{x}^{n}}}=x$ .
If n is even, $\sqrt[n]{{{x}^{n}}}=\left| x \right|$ . (The absolute value accounts for the fact that if x is negative and raised to an even power, that number will be positive, as will the nth principal root of that number.)

Module 9: Radical Functions and Rational Exponents

9.2 – Radical Expressions and Rational Exponents

Learning Objectives

(9.2.1) – Define and identify a radical expression

(9.2.2) – Convert radicals to expressions with rational exponents

Example

Answer

Example

Answer

(9.2.3) – Convert expressions with rational exponents to their radical equivalent

Example

Answer

Example

Answer

(9.2.4) – Rational exponents whose numerator is not equal to one

Writing Rational Exponents

Example

Answer

Answer

Example

(9.2.5) – Simplify Radical Expressions

A Product Raised to a Power Rule or sometimes called The Square Root of a Product Rule

Simplify radical expressions using factoring

Example

Taking the Square Root of a Radical Expression

Example

Answer

Analysis of the Solution

Example

Answer

ExAMPLE

Answer

Analysis of the solution:

Example

Answer

Example

Answer

Simplify cube roots

Example

Answer

Example

Answer

Analysis of the solution

Example

Answer

Analysis of the solution

Simplifying fourth roots

Example

Answer

Simplify radical expressions using rational exponents and the laws of exponents

Example

Answer

Example

Answer

Summary

Simplifying a radical