Learning Objectives
- (7.5.1) – Solving polynomial equations
- The principle of zero products
- (7.5.2) – Applications of polynomial equations
- Projectile motion
- Using the Pythagorean theorem to find the lengths of a right triangle
- Geometric Applications
- Cost, revenue, and profit polynomials
(7.5.1) – Solving polynomial equations
Not all of the techniques we use for solving linear equations will apply to solving polynomial equations. In this section we will introduce a method for solving polynomial equations that combines factoring and the zero product principle.
The Principle of Zero Products

Zero
What if we told you that we multiplied two numbers together and got an answer of zero? What could you say about the two numbers? Could they be 2 and 5? Could they be 9 and 1? No! When the result (answer) from multiplying two numbers is zero, that means that one of them had to be zero. This idea is called the zero product principle, and it is useful for solving polynomial equations that can be factored.
Principle of Zero Products
The Principle of Zero Products states that if the product of two numbers is 0, then at least one of the factors is 0. If [latex]ab=0[/latex], then either [latex]a=0[/latex] or [latex]b=0[/latex], or both [latex]a[/latex] and [latex]b[/latex] are 0.
Let’s start with a simple example. We will factor a GCF from a binomial and apply the principle of zero products to solve a polynomial equation.
Example
Solve:
[latex]-t^2+t=0[/latex]
In the following video we show two more examples of using both factoring and the principle of zero products to solve a polynomial equation.
In the next video we show that you can factor a trinomial using methods previously learned to solve a quadratic equation.
You and I both know that it is rare to be given an equation to solve that has zero on one side, so let’s try another one.
Example
Solve: [latex]s^2-4s=5[/latex]
We will work through one more example that is similar to the one above, except this example has fractions.
Example
Solve [latex]y^2-5=-\frac{7}{2}y+\frac{5}{2}[/latex]
In our last video, we show how to solve another quadratic equation that contains fractions.
(7.5.2) – Applications of polynomial equations
Projectile Motion
Projectile motion happens when you throw a ball into the air and it comes back down because of gravity. A projectile will follow a curved path that behaves in a predictable way. This predictable motion has been studied for centuries, and in simple cases it’s height from the ground at a given time, [latex]t[/latex], can be modeled with a polynomial function of the form [latex]h(t)=at^2+bt+c[/latex], where h(t) = height of an object at a given time, [latex]t[/latex]. Projectile motion is also called a parabolic trajectory because of the shape of the path of a projectile’s motion, as in the image of water in the fountain below.

Parabolic WaterTrajectory
Parabolic motion and it’s related functions allow us to launch satellites for telecommunications, and rockets for space exploration. Recently, police departments have even begun using projectiles with GPS to track fleeing suspects in vehicles, rather than pursuing them by high-speed chase [1].
In this section we will use polynomial functions to answer questions about the parabolic motion of a projectile. The real mathematical model for the path of a rocket or a police GPS projectile may have different coefficients or more variables, but the concept remains the same. We will also learn to interpret the meaning of the variables in a polynomial function that models projectile motion.
Example
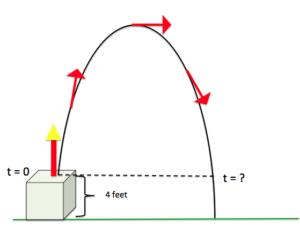
A small toy rocket is launched from a 4-foot pedestal. The height ([latex]h[/latex], in feet) of the rocket [latex]t[/latex] seconds after taking off is given by the function [latex]h(t)=−2t^{2}+7t+4[/latex]. How long will it take the rocket to hit the ground?
In the next example we will solve for the time that the rocket is at a given height other than zero.
Example
Use the formula for the height of the rocket in the previous example to find the time when the rocket is 4 feet from hitting the ground on it’s way back down. Refer to the image.
[latex]h(t)=−2t^{2}+7t+4[/latex]
In the following video we show another example of how to find the time when a object following a parabolic trajectory hits the ground.
In this section we introduced the concept of projectile motion, and showed that it can be modeled with polynomial function. While the models used in these examples are simple, the concepts and interpretations are the same as what would happen in “real life”.
Pythagorean Theorem
The Pythagorean theorem or Pythagoras’s theorem is a statement about the sides of a right triangle. One of the angles of a right triangle is always equal to 90 degrees. This angle is the right angle. The two sides next to the right angle are called the legs and the other side is called the hypotenuse. The hypotenuse is the side opposite to the right angle, and it is always the longest side. The image above shows four common kinds of triangle, including a right triangle.
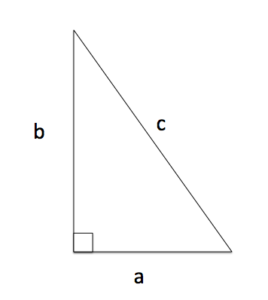
Right Triangle Labeled
The Pythagorean theorem is often used to find unknown lengths of the sides of right triangles. If the longest leg of a right triangle is labeled c, and the other two a, and b as in the image on teh left, The Pythagorean Theorem states that
[latex]a^2+b^2=c^2[/latex]
Given enough information, we can solve for an unknown length. This relationship has been used for many, many years for things such as celestial navigation and early civil engineering projects. We now have digital GPS and survey equipment that have been programmed to do the calculations for us.
In the next example we will combine the power of the Pythagorean theorem and what we know about solving quadratic equations to find unknown lengths of right triangles.
Example
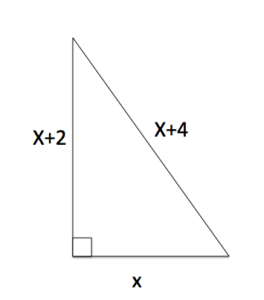
A right triangle has one leg with length [latex]x[/latex], another whose length is greater by two, and the length of the hypotenuse is greater by four. Find the lengths of the sides of the triangle. Use the image below.
This video example shows another way a quadratic equation can be used to find and unknown length of a right triangle.
Geometric Applications
In this section we will explore ways that polynomials are used in applications of area problems.
Example
The length of a rectangle is 3 more than the width. If the area is 40 square inches, what are the dimensions?
In the following video you are shown how to find the dimensions of a border around a rectangle.
Try It
Cost, Revenue, and Profit Polynomials
In the systems of linear equations section, we discussed how a company’s cost and revenue can be modeled with two linear equations. We found that the profit region for a company was the area between the two lines where the company would make money based on how much was produced. In this section, we will see that sometimes polynomials are used to describe cost and revenue.
Profit is typically defined in business as the difference between the amount of money earned (revenue) by producing a certain number of items and the amount of money it takes to produce that number of items. When you are in business, you definitely want to see profit, so it is important to know what your cost and revenue is.

Cell Phones
For example, let’s say that the cost to a manufacturer to produce a certain number of things is C and the revenue generated by selling those things is R. The profit, P, can then be defined as
P = R-C
The example we will work with is a hypothetical cell phone manufacturer whose cost to manufacture x number of phones is [latex]C=2000x+750,000[/latex], and the Revenue generated from manufacturing x number of cell phones is [latex]R=-0.09x^2+7000x[/latex].
Example
Define a Profit polynomial for the hypothetical cell phone manufacturer.
Mathematical models are great when you use them to learn important information. The cell phone manufacturing company can use the profit equation to find out how much profit they will make given [latex]x[/latex] number of phones are manufactured. In the next example, we will explore some profit values for this company.
Example
Given the following numbers of cell phones manufactured, find the profit for the cell phone manufacturer:
- x = 100 phones
- x = 25,000 phones
- x=60,000 phones
Interpret your results.
In the video that follows, we present another example of finding a polynomial profit equation.
Candela Citations
- Solve a Quadratic Equations with Fractions by Factoring (a not 1). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/kDj_qdKW-ls. License: CC BY: Attribution
- Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
- Parabolic motion description and example. Provided by: Lumen Learning. License: CC BY: Attribution
- Factoring Application - Find the Time When a Projectile Hits and Ground. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/hsWSzu3KcPU. License: CC BY: Attribution
- Pythagorean Theorem, Description and Examples. Provided by: Lumen Learning. License: CC BY: Attribution
- Screenshot: Thumbsdown. Provided by: Lumen Learning. License: CC BY: Attribution
- Screenshot PI. Provided by: Lumen Learning. License: CC BY: Attribution
- Polynomial Multiplication Application - Volume of a Cylinder. . Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/g-g_nSsfGs4. License: CC BY: Attribution
- Polynomial Subtracton App - Profit Equation from Revene and Cost.. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning.. Located at: https://youtu.be/-TWjDC4g9dU. License: CC BY: Attribution
- Screenshot: Cell Phones.. Authored by: Lumen Learning. License: CC BY: Attribution
- Profit Polynomial Examples. Provided by: Lumen Learning. License: CC BY: Attribution
- Ex: Factor and Solve Quadratic Equation - Greatest Common Factor Only. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/gIwMkTAclw8. License: CC BY: Attribution
- Ex: Factor and Solve Quadratic Equations When A equals 1. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/bi7i_RuIGl0. License: CC BY: Attribution
- Unit 12: Factoring, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology. Located at: http://nrocnetwork.org/dm-opentext. License: CC BY: Attribution
- Parabolic water trajectory. Authored by: By GuidoB. Located at: https://commons.wikimedia.org/w/index.php?curid=8015696. License: CC BY-SA: Attribution-ShareAlike
- Pythagorean Theorem. Provided by: Wikipedia. Located at: https://en.wikipedia.org/wiki/Pythagorean_theorem. License: CC BY-SA: Attribution-ShareAlike
- Ex: Polynomial Addition Application - Perimeter.. Authored by: James Sousa (Mathispower4u.com). . Located at: https://youtu.be/BhRpZv0_0jE. License: CC BY: Attribution
- Ex: Find the Area of a Rectangle Using a Polynomial.. Authored by: James Sousa (Mathispower4u.com) .. Located at: https://youtu.be/5Q2htATOIik. License: CC BY: Attribution
- Unit 11: Exponents and Polynomials, from Developmental Math: An Open Program. . Provided by: Monterey Institute of Technology and Education. Located at: http://nrocnetwork.org/dm-opentext. License: CC BY: Attribution
- Applied Optimization Problems. Provided by: OpenStax. Located at: http://cnx.org/contents/svyieFe9@2/Applied-Optimization-Problems. License: CC BY-NC-SA: Attribution-NonCommercial-ShareAlike. License Terms: Download for free at http://cnx.org/contents/b2fca278-57bd-421d-aa85-21f539b4cc6f@2
- Applications of Quadratic Equations. Authored by: James Sousa. Located at: http://www.youtube.com/watch?v=AlIoxXQ-V50. License: CC BY: Attribution
- Quadratics - Rectangle. Authored by: Tyler Wallace. Located at: http://wallace.ccfaculty.org/book/book.html. Project: Beginning and Intermediate Algebra. License: Public Domain: No Known Copyright
- Question ID#74417. Authored by: Nearing,Daniel. License: CC BY: Attribution
- Celestial Navigation Math. Authored by: TabletClass Math. Located at: https://www.youtube.com/watch?v=XWLZKmPU17M. License: All Rights Reserved. License Terms: Standard YouTube License
- "Cops' Latest Tool in High-speed Chases: GPS Projectiles." CBSNews. CBS Interactive, n.d. Web. 14 June 2016. ↵
