Learning Outcomes
- Create a table of ordered pairs from a two-variable linear equation
- Graph a two-variable linear equation using a table of ordered pairs
- Determine whether an ordered pair is a solution of an equation
You have likely used a coordinate plane before. The coordinate plane consists of a horizontal axis and a vertical axis, number lines that intersect at right angles. (They are perpendicular to each other.)
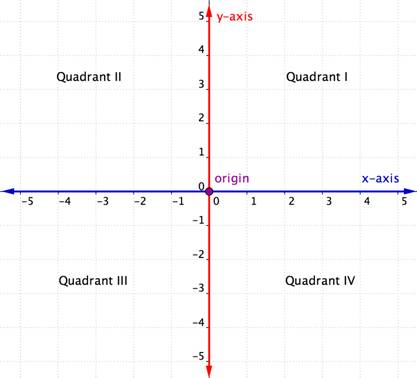
The horizontal axis in the coordinate plane is called the x-axis. The vertical axis is called the y-axis. The point at which the two axes intersect is called the origin. The origin is at [latex]0[/latex] on the x-axis and [latex]0[/latex] on the y-axis.
Locations on the coordinate plane are described as ordered pairs. An ordered pair tells you the location of a point by relating the point’s location along the x-axis (the first value of the ordered pair) and along the y-axis (the second value of the ordered pair).
In an ordered pair, such as (x, y), the first value is called the x-coordinate and the second value is the y-coordinate. Note that the x-coordinate is listed before the y-coordinate. Since the origin has an x-coordinate of [latex]0[/latex] and a y-coordinate of [latex]0[/latex], its ordered pair is written as ([latex]0, 0[/latex]).
Consider the point below.
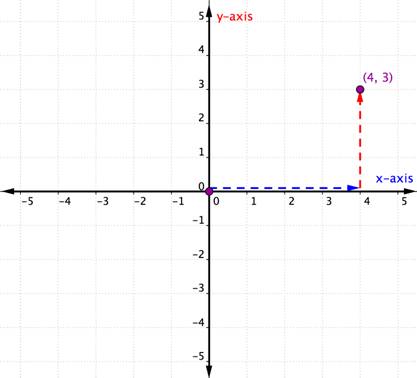
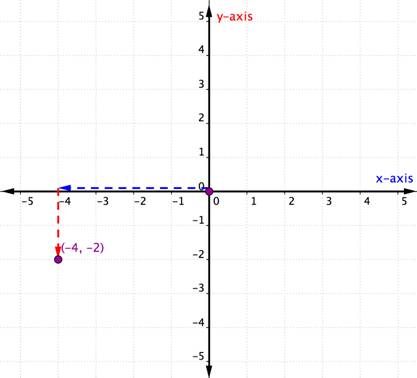
To identify the location of this point, start at the origin ([latex]0, 0[/latex]) and move right along the x-axis until you are under the point. Look at the label on the x-axis. The [latex]4[/latex] indicates that, from the origin, you have traveled four units to the right along the x-axis. This is the x-coordinate, the first number in the ordered pair.
From [latex]4[/latex] on the x-axis move up to the point and notice the number with which it aligns on the y-axis. The [latex]3[/latex] indicates that, after leaving the x-axis, you traveled [latex]3[/latex] units up in the vertical direction, the direction of the y-axis. This number is the y-coordinate, the second number in the ordered pair. With an x-coordinate of [latex]4[/latex] and a y-coordinate of [latex]3[/latex], you have the ordered pair ([latex]4, 3[/latex]).
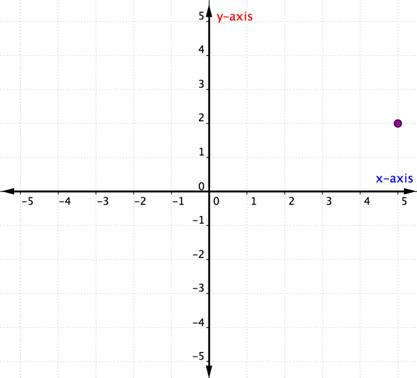
Example
Describe the point shown as an ordered pair.
Example
Plot the point [latex](−4,−2)[/latex].
Graphing ordered pairs is only the beginning of the story. Once you know how to place points on a grid, you can use them to make sense of all kinds of mathematical relationships.
You can use a coordinate plane to plot points and to map various relationships such as the relationship between an object’s distance and the elapsed time. Many mathematical relationships are linear relationships. Let us look at what a linear relationship is.
Plotting Points to Graph Linear Relationships
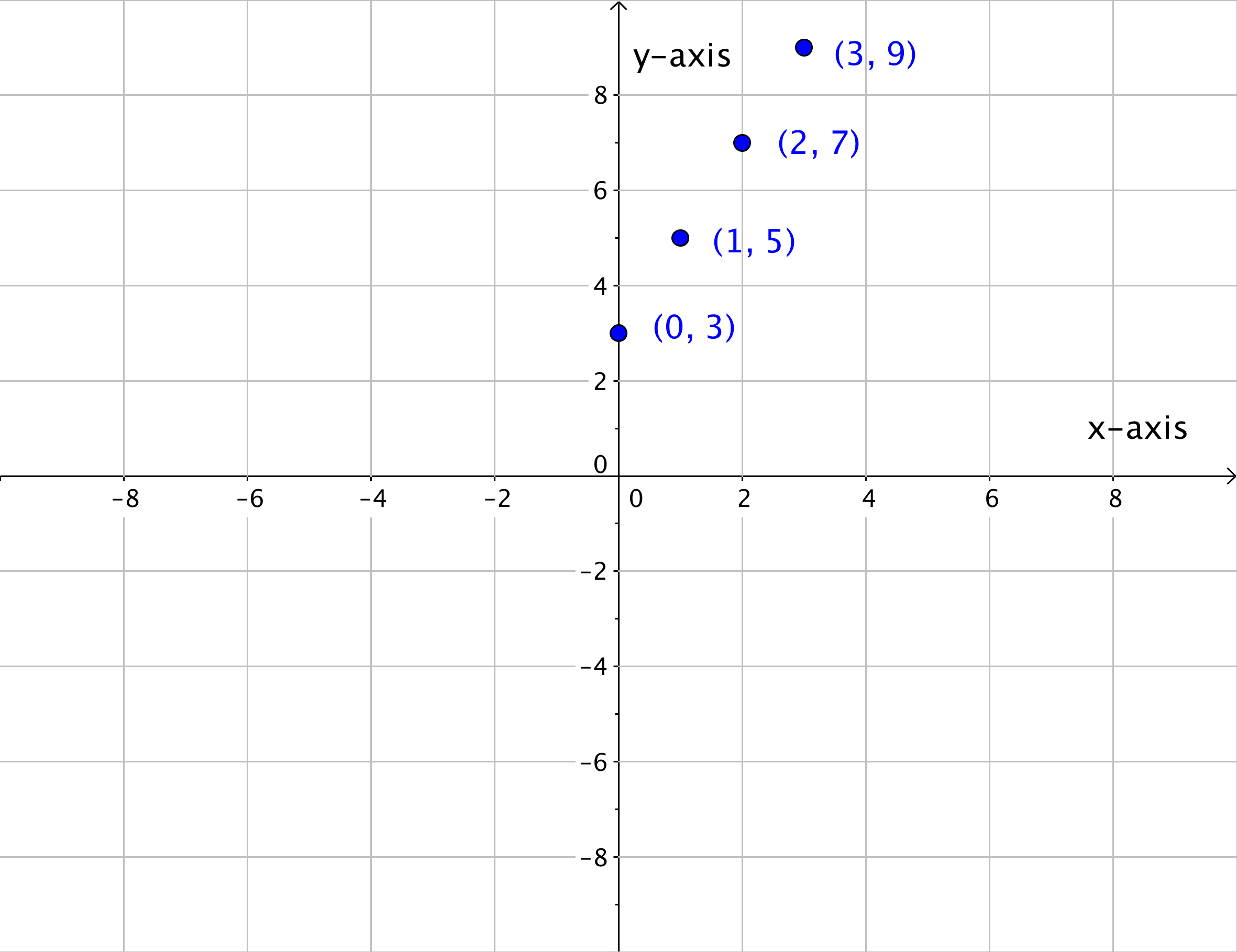
A linear relationship is a relationship between variables such that when plotted on a coordinate plane, the points lie on a line. Start by looking at a series of points in Quadrant I on the coordinate plane.
These series of points can also be represented in a table. In the table below, the x- and y-coordinates of each ordered pair on the graph is recorded.
| x-coordinate | y-coordinate |
| [latex]0[/latex] | [latex]0[/latex] |
| [latex]1[/latex] | [latex]2[/latex] |
| [latex]2[/latex] | [latex]4[/latex] |
| [latex]3[/latex] | [latex]6[/latex] |
| [latex]4[/latex] | [latex]8[/latex] |
Notice that each y-coordinate is twice the corresponding x-value. All of these x- and y-values follow the same pattern, and, when placed on a coordinate plane, they all line up as shown below.
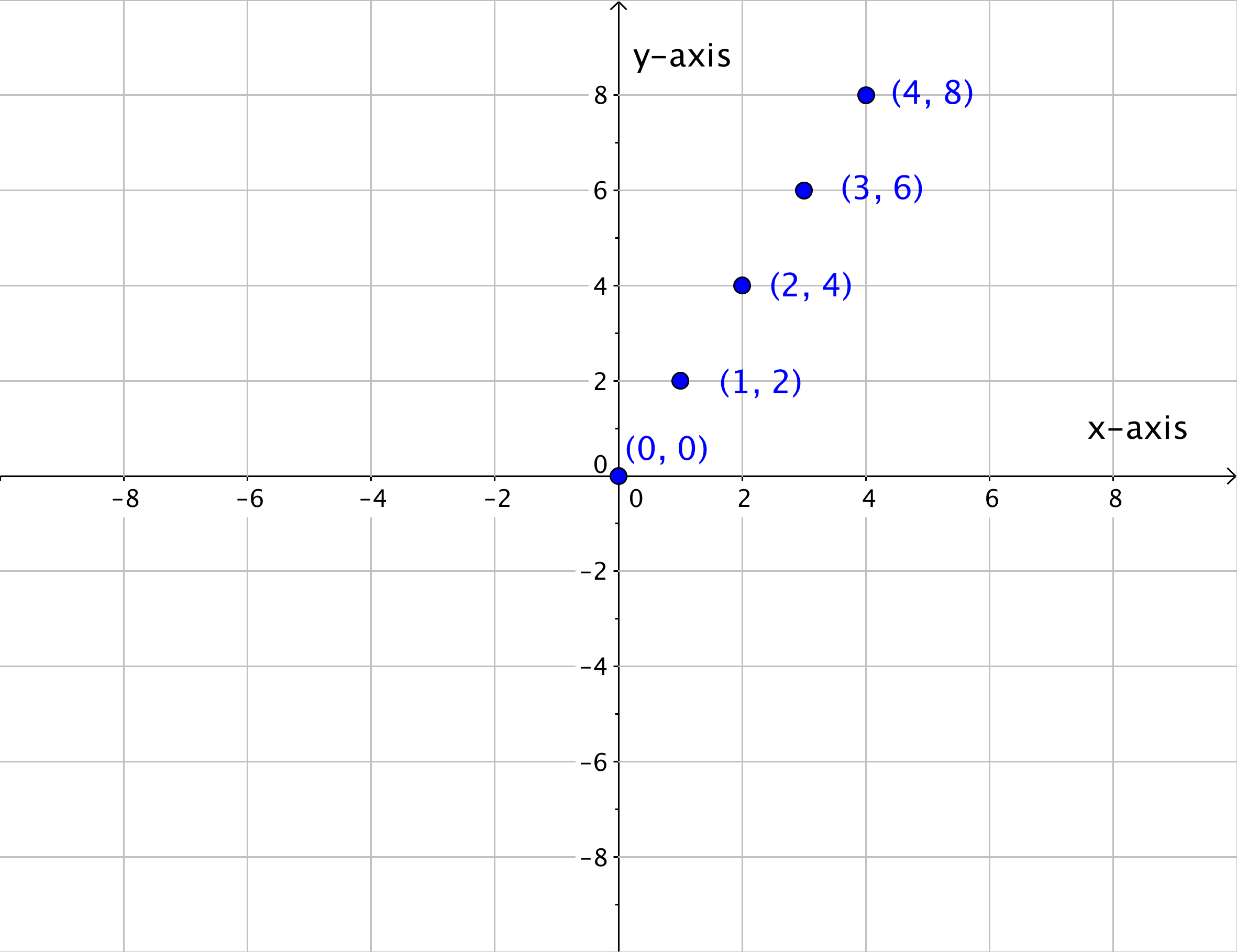
Once you know the pattern that relates the x- and y-values, you can find a y-value for any x-value that lies on the line. So if the rule of this pattern is that each y-coordinate is twice the corresponding x-value, then the ordered pairs ([latex]1.5, 3[/latex]), ([latex]2.5, 5[/latex]), and ([latex]3.5, 7[/latex]) should all appear on the line too, correct? Look to see what happens below.
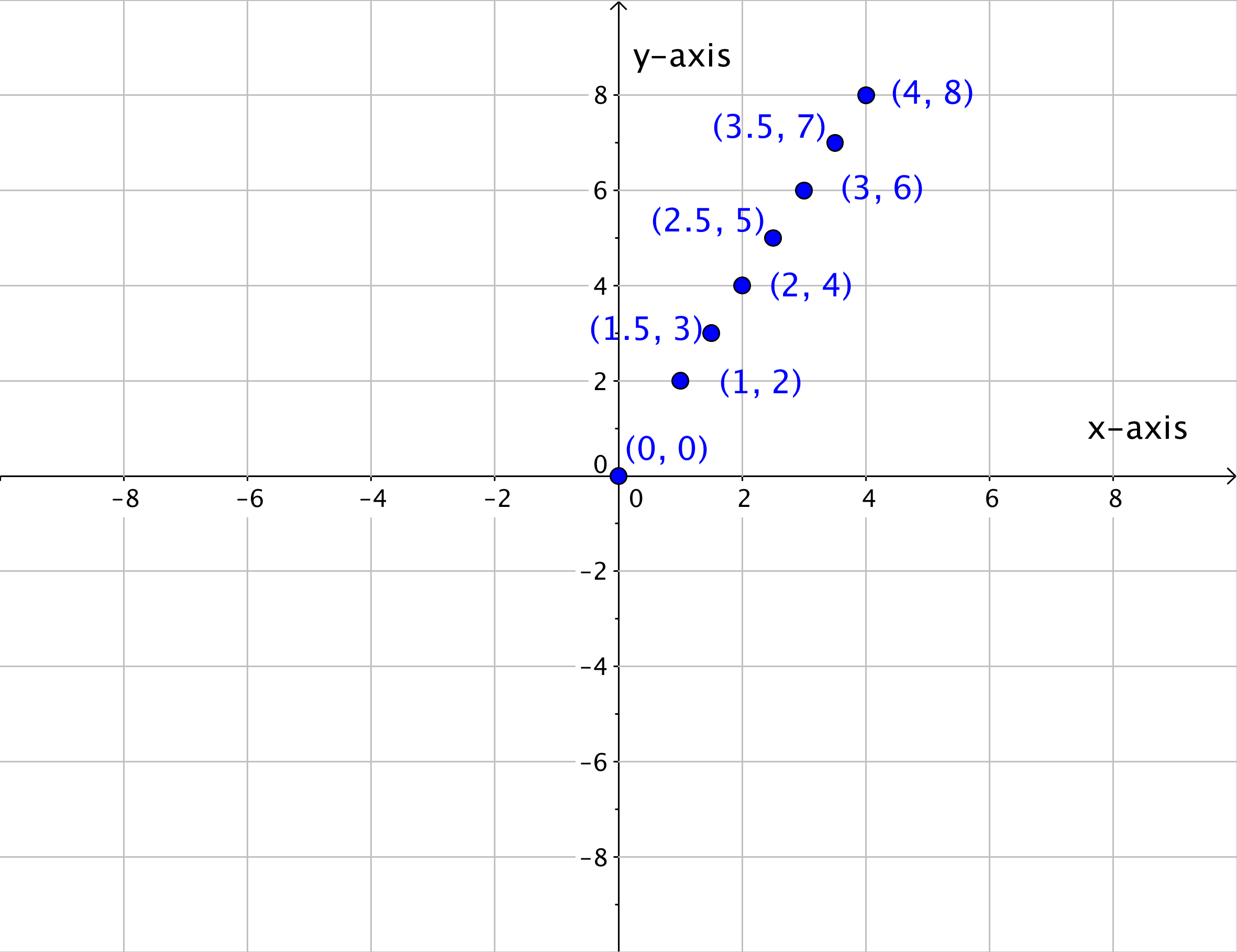
If you were to keep adding ordered pairs (x, y) where the y-value was twice the x-value, you would end up with the graph seen below.
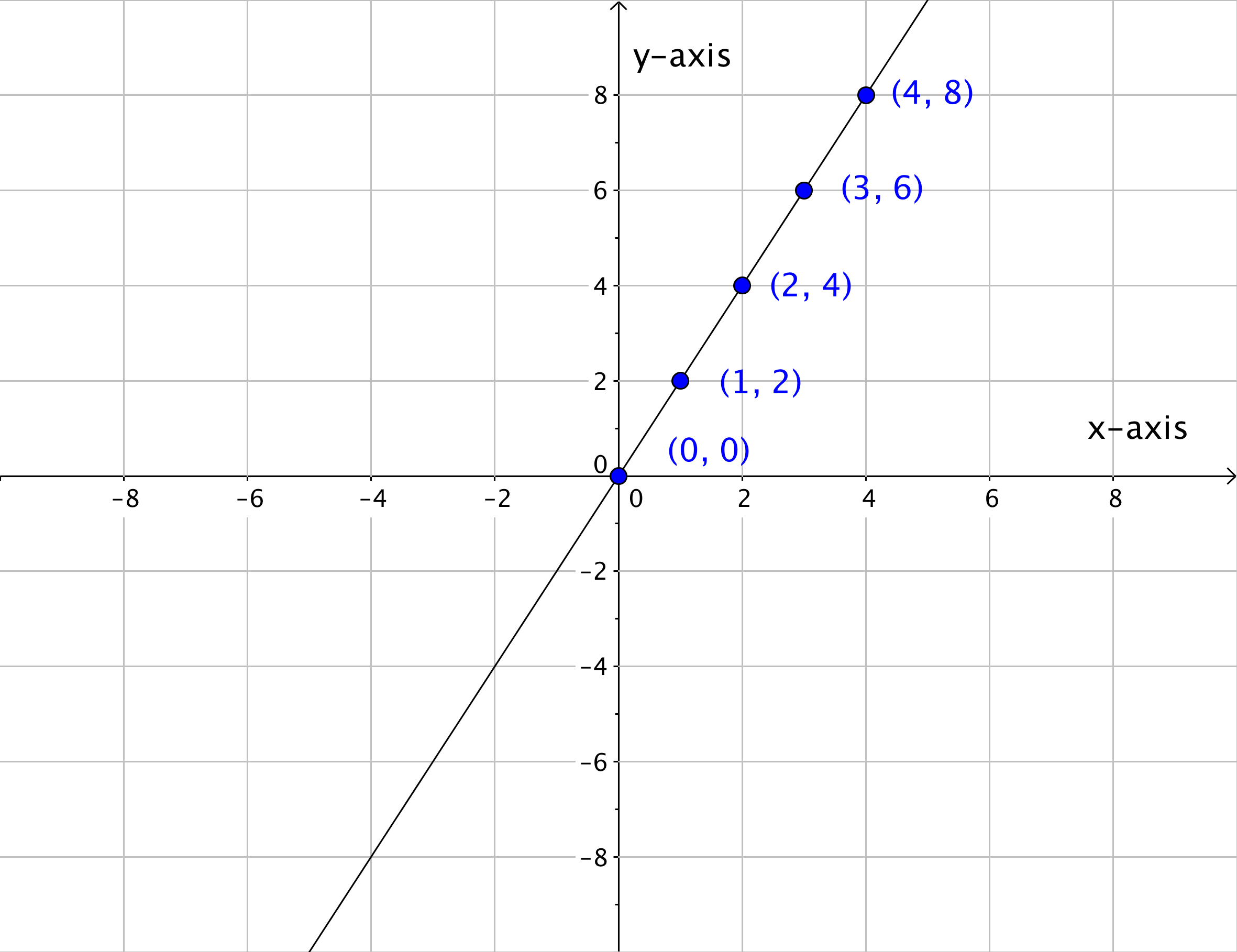
Look at how all of the points blend together to create a line. You can think of a line, then, as a collection of an infinite number of individual points that share the same mathematical relationship. In this case, the relationship is that the y-value is twice the x-value.
There are multiple ways to represent a linear relationship—a table, a linear graph, and there is also a linear equation. A linear equation is an equation with two variables whose ordered pairs graph a straight line.
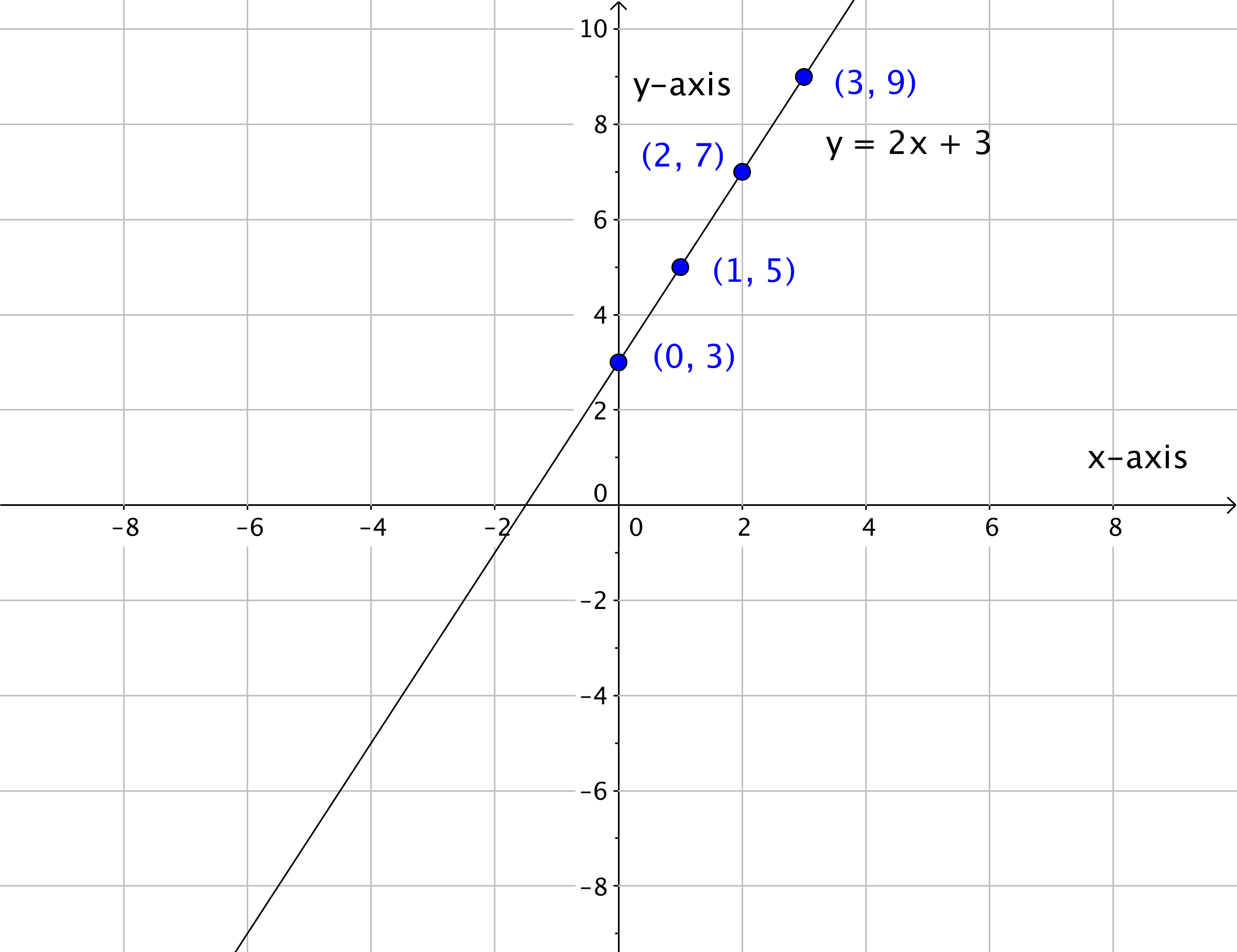
There are several ways to create a graph from a linear equation. One way is to create a table of values for x and y and then plot these ordered pairs on the coordinate plane. Two points are enough to determine a line. However, it is always a good idea to plot more than two points to avoid possible errors.
After graphing the points, draw a line through the points to show that all of the points are on the line. The arrows at each end of the graph indicate that the line continues endlessly in both directions. Every point on this line is a solution to the linear equation.
Example
Graph the linear equation [latex]y=2x+3[/latex].
Ordered Pairs as Solutions
So far, you have considered the following ideas about lines: a line is a visual representation of a linear equation, and the line itself is made up of an infinite number of points (or ordered pairs). The picture below shows the line of the linear equation [latex]y=2x–5[/latex] with some of the specific points on the line.
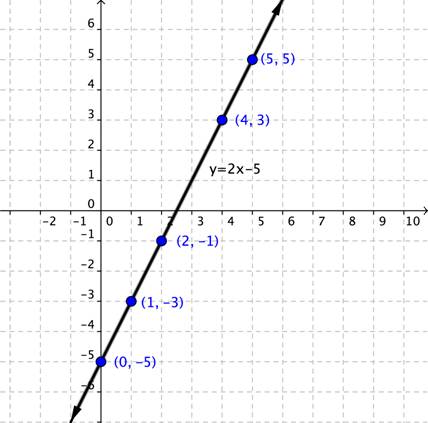
Every point on the line is a solution to the equation [latex]y=2x–5[/latex]. You can plug the ordered pair [latex](1,−3)[/latex] into the equation and the equation will be satisfied.
[latex]\begin{array}{l}\,\,\,\,y=2x-5\\-3=2\left(1\right)-5\\-3=2-5\\-3=-3\\\text{This is true.}\end{array}[/latex]
You can also plug ANY of the other points on the line into the equation. Every point on the line is a solution to the equation [latex]y=2x–5[/latex]. All this means is that determining whether an ordered pair is a solution of an equation is pretty straightforward. If the ordered pair is on the line created by the linear equation, then it is a solution to the equation. But if the ordered pair is not on the line—no matter how close it may look—then it is not a solution to the equation.
To find out whether an ordered pair is a solution of a linear equation, you can do the following:
- Graph the linear equation and graph the ordered pair. If the ordered pair appears to be on the graph of a line, then it is a possible solution of the linear equation. If the ordered pair does not lie on the graph of a line, then it is not a solution.
- Substitute the (x, y) values into the equation. If the equation yields a true statement, then the ordered pair is a solution of the linear equation. If the ordered pair does not yield a true statement then it is not a solution.
Example
Determine whether [latex](−2,4)[/latex] is a solution to the equation [latex]4y+5x=3[/latex].
Below is a video further explaining how to determine if an ordered pair is a solution to a linear equation.