Just as with systems of equations in two variables, we may come across an inconsistent system of equations in three variables, which means that it does not have a solution that satisfies all three equations. The equations could represent three parallel planes, two parallel planes and one intersecting plane, or three planes that intersect the other two but not at the same location. The process of elimination will result in a false statement, such as [latex]3=7[/latex] or some other contradiction.

Infinitely Many or No Solutions

 

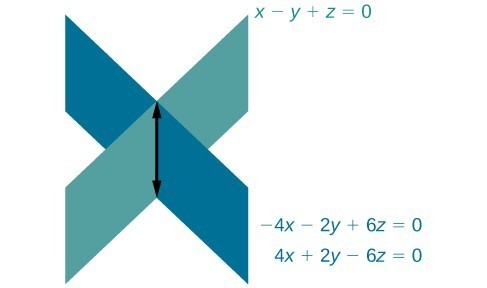
• Systems that have an infinite number of solutions are those which, after elimination, result in an expression that is always true, such as [latex]0=0[/latex]. Graphically, an infinite number of solutions represents a line or coincident plane that serves as the intersection of three planes in space. The graphic below shows how three planes can intersect to form a line giving the system infinitely many solutions.

Infinitely many solutions.

 

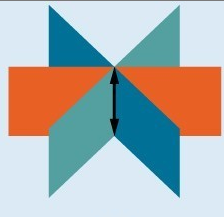
• Systems that have no solution are those that, after elimination, result in a statement that is a contradiction, such as [latex]3=0[/latex]. Graphically, a system with no solution is represented by three planes with no point in common. Three parallel planes (c), two parallel planes and one intersecting plane (b), three planes that intersect the other two but not at the same location (a).

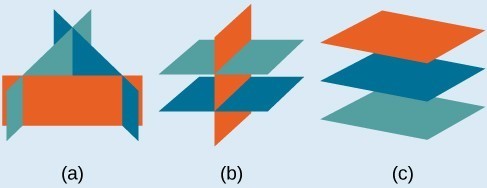
In the first example, we will see how it is possible to have a system with three variables and no solutions.

We will show another example of using elimination to solve a system in three variables that ends up having no solution in the following video.

We know from working with systems of equations in two variables that a dependent system of equations has an infinite number of solutions. The same is true for dependent systems of equations in three variables. An infinite number of solutions can result from several situations. The three planes could be the same so that a solution to one equation will be the solution to the other two equations. All three equations could be different but they intersect on a line, which has infinite solutions. The other possibility is that two of the equations could be the same and intersect the third on a line.

Example

Find the solution to the given system of three equations in three variables.

[latex]\begin{array}{rr}\hfill \text{ }2x+y - 3z=0& \hfill \left(1\right)\\ \hfill 4x+2y - 6z=0& \hfill \left(2\right)\\ \hfill \text{ }x-y+z=0& \hfill \left(3\right)\end{array}[/latex]

Show Solution

First, we can multiply equation [latex](1)[/latex] by [latex]-2[/latex] and add it to equation [latex](2)[/latex].

[latex]\begin{array} −4x−2y+6z=0 \hfill& \text{equation }\left(1\right)\text{multiplied by }−2 \\ 4x+2y−6z=0\hfill&\left(2\right) \end{array}[/latex]

We do not need to proceed any further. The result we get when adding the two equations is an identity, [latex]0=0[/latex] which tells us that this system has an infinite number of solutions.

As shown in the figure below, two of the planes are the same and they intersect the third plane on a line. The solution set is infinite, as all points along the intersection line will satisfy all three equations.

In our last video example, we show a system that has an infinite number of solutions.

Summary

• A system with three variables can have one, none, or many solutions.
• A system with no solutions will have a non-true result when solving.
• A system with many solutions will have an identity result when solving.