Learning Outcomes
- Solve systems of three equations in three variables
The solution set to a system of three equations in three variables is an ordered triple [latex]\left(x,y,z\right)[/latex]. Graphically, the ordered triple defines the point that is the intersection of three planes in space. You can visualize such an intersection by imagining any corner in a rectangular room. A corner is defined by three planes: two adjoining walls and the floor (or ceiling). Any point where two walls and the floor meet represents the intersection of three planes.
Solution Set, One Solution
The figure below illustrates how a system with three variables can have one solution. Systems that have a single solution are those which result in a solution set consisting of an ordered triple [latex]\left(x,y,z\right)[/latex]. Graphically, the ordered triple defines a point that is the intersection of three planes in space.
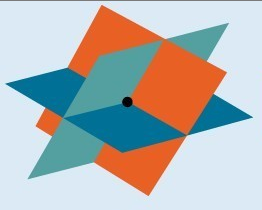
In the first example, we will determine whether an ordered triple is a solution for a system of three linear equations in three variables.
Example
Determine whether the ordered triple [latex]\left(3,-2,1\right)[/latex] is a solution to the system.
How To: Given a linear system of three equations, solve for three unknowns
- Pick any pair of equations and solve for one variable.
- Pick another pair of equations and solve for the same variable.
- You have created a system of two equations in two unknowns. Solve the resulting two-by-two system.
- Back-substitute known variables into any one of the original equations and solve for the missing variable.
Solving a system with three variables is very similar to solving one with two variables. It is important to keep track of your work as the addition of one more equation can create more steps in the solution process.
In the example that follows, we will solve the system by first using the elimination method to solve for x and then using back-substitution.
Example
Solve the given system.
[latex]\displaystyle\begin{cases}x-\dfrac{1}{3}y+\dfrac{1}{2}z=1\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,y-\dfrac{1}{2}z=4\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,z=-1\end{cases}[/latex]
Analysis of the Solution:
Each of the lines in the system above represents a plane (think about a sheet of paper). If you imagine three sheets of notebook paper each representing a portion of these planes, you will start to see the complexities involved in how three such planes can intersect. Below is a sketch of the three planes. It turns out that any two of these planes intersect in a line, so our intersection point is where all three of these lines meet.
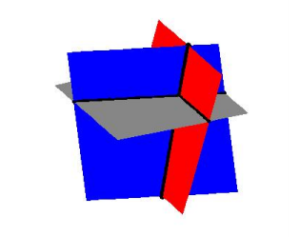
Three planes intersecting.
In the following video, we show another example of using back-substitution to solve a system in three variables.
In the next example, we will not start with a solution, but will need to use the method of elimination to find our first solution.
Example
Find a solution to the following system:
In the following videos, we show more examples of the algebra you may encounter when solving systems with three variables.
Summary
- The solution to a system of linear equations in three variables is an ordered triple of the form [latex](x,y,z)[/latex].
- Solutions can be verified using substitution and the order of operations.
- Systems of three variables can be solved using the same techniques as we used to solve systems with two variables, including elimination and substitution.
