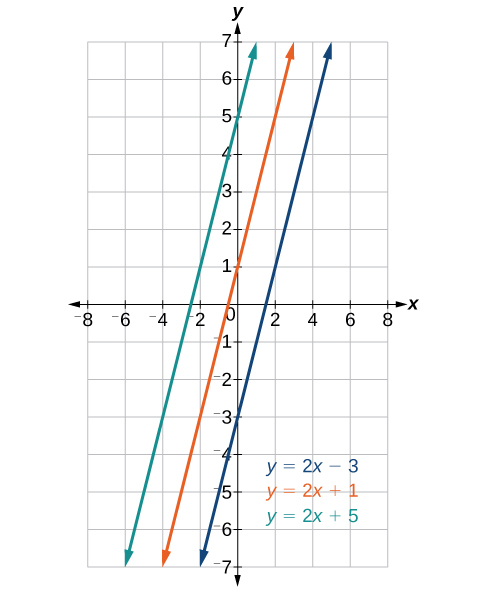
Figure 4. Parallel lines
Parallel lines have the same slope and different y-intercepts. Lines that are parallel to each other will never intersect. For example, Figure 4 shows the graphs of various lines with the same slope, [latex]m=2[/latex].
All of the lines shown in the graph are parallel because they have the same slope and different y-intercepts.
Lines that are perpendicular intersect to form a [latex]{90}^{\circ }[/latex] -angle. The slope of one line is the negative reciprocal of the other. We can show that two lines are perpendicular if the product of the two slopes is [latex]-1:{m}_{1}\cdot {m}_{2}=-1[/latex]. For example, Figure 4 shows the graph of two perpendicular lines. One line has a slope of 3; the other line has a slope of [latex]-\frac{1}{3}[/latex].

Figure 5. Perpendicular lines
Example 13: Graphing Two Equations, and Determining Whether the Lines are Parallel, Perpendicular, or Neither
Graph the equations of the given lines, and state whether they are parallel, perpendicular, or neither: [latex]3y=-4x+3[/latex] and [latex]3x - 4y=8[/latex].
Solution
The first thing we want to do is rewrite the equations so that both equations are in slope-intercept form.
First equation:
Second equation:
See the graph of both lines in Figure 6.

Figure 6
From the graph, we can see that the lines appear perpendicular, but we must compare the slopes.
The slopes are negative reciprocals of each other, confirming that the lines are perpendicular.
Try It 11
Graph the two lines and determine whether they are parallel, perpendicular, or neither: [latex]2y-x=10[/latex] and [latex]2y=x+4[/latex].
Writing the Equations of Lines Parallel or Perpendicular to a Given Line
As we have learned, determining whether two lines are parallel or perpendicular is a matter of finding the slopes. To write the equation of a line parallel or perpendicular to another line, we follow the same principles as we do for finding the equation of any line. After finding the slope, use the point-slope formula to write the equation of the new line.
How To: Given an equation for a line, write the equation of a line parallel or perpendicular to it.
- Find the slope of the given line. The easiest way to do this is to write the equation in slope-intercept form.
- Use the slope and the given point with the point-slope formula.
- Simplify the line to slope-intercept form and compare the equation to the given line.
Example 14: Writing the Equation of a Line Parallel to a Given Line Passing Through a Given Point
Write the equation of line parallel to a [latex]5x+3y=1[/latex] and passing through the point [latex]\left(3,5\right)[/latex].
Solution
First, we will write the equation in slope-intercept form to find the slope.
The slope is [latex]m=-\frac{5}{3}[/latex]. The y-intercept is [latex]\frac{1}{3}[/latex], but that really does not enter into our problem, as the only thing we need for two lines to be parallel is the same slope. The one exception is that if the y-intercepts are the same, then the two lines are the same line. The next step is to use this slope and the given point with the point-slope formula.
The equation of the line is [latex]y=-\frac{5}{3}x+10[/latex].

Figure 7
Try It 12
Find the equation of the line parallel to [latex]5x=7+y[/latex] and passing through the point [latex]\left(-1,-2\right)[/latex].
Example 15: Finding the Equation of a Line Perpendicular to a Given Line Passing Through a Given Point
Find the equation of the line perpendicular to [latex]5x - 3y+4=0\left(-4,1\right)[/latex].
Solution
The first step is to write the equation in slope-intercept form.
We see that the slope is [latex]m=\frac{5}{3}[/latex]. This means that the slope of the line perpendicular to the given line is the negative reciprocal, or [latex]-\frac{3}{5}[/latex]. Next, we use the point-slope formula with this new slope and the given point.