Perhaps the most familiar form of a linear equation is the slope-intercept form, written as [latex]y=mx+b[/latex], where [latex]m=\text{slope}[/latex] and [latex]b=y\text{-intercept}[/latex]. Let us begin with the slope.
The Slope of a Line
The slope of a line refers to the ratio of the vertical change in y over the horizontal change in x between any two points on a line. It indicates the direction in which a line slants as well as its steepness. Slope is sometimes described as rise over run.
If the slope is positive, the line slants to the right. If the slope is negative, the line slants to the left. As the slope increases, the line becomes steeper. Some examples are shown in Figure 2. The lines indicate the following slopes: [latex]m=-3[/latex], [latex]m=2[/latex], and [latex]m=\frac{1}{3}[/latex].

Figure 2
A General Note: The Slope of a Line
The slope of a line, m, represents the change in y over the change in x. Given two points, [latex]\left({x}_{1},{y}_{1}\right)[/latex] and [latex]\left({x}_{2},{y}_{2}\right)[/latex], the following formula determines the slope of a line containing these points:
Example 7: Finding the Slope of a Line Given Two Points
Find the slope of a line that passes through the points [latex]\left(2,-1\right)[/latex] and [latex]\left(-5,3\right)[/latex].
Solution
We substitute the y-values and the x-values into the formula.
The slope is [latex]-\frac{4}{7}[/latex].
Analysis of the Solution
It does not matter which point is called [latex]\left({x}_{1},{y}_{1}\right)[/latex] or [latex]\left({x}_{2},{y}_{2}\right)[/latex]. As long as we are consistent with the order of the y terms and the order of the x terms in the numerator and denominator, the calculation will yield the same result.
Try It 7
Find the slope of the line that passes through the points [latex]\left(-2,6\right)[/latex] and [latex]\left(1,4\right)[/latex].
Example 8: Identifying the Slope and y-intercept of a Line Given an Equation
Identify the slope and y-intercept, given the equation [latex]y=-\frac{3}{4}x - 4[/latex].
Solution
As the line is in [latex]y=mx+b[/latex] form, the given line has a slope of [latex]m=-\frac{3}{4}[/latex]. The y-intercept is [latex]b=-4[/latex].
Analysis of the Solution
The y-intercept is the point at which the line crosses the y-axis. On the y-axis, [latex]x=0[/latex]. We can always identify the y-intercept when the line is in slope-intercept form, as it will always equal b. Or, just substitute [latex]x=0[/latex] and solve for y.
The Point-Slope Formula
Given the slope and one point on a line, we can find the equation of the line using the point-slope formula.
This is an important formula, as it will be used in other areas of college algebra and often in calculus to find the equation of a tangent line. We need only one point and the slope of the line to use the formula. After substituting the slope and the coordinates of one point into the formula, we simplify it and write it in slope-intercept form.
A General Note: The Point-Slope Formula
Given one point and the slope, the point-slope formula will lead to the equation of a line:
Example 9: Finding the Equation of a Line Given the Slope and One Point
Write the equation of the line with slope [latex]m=-3[/latex] and passing through the point [latex]\left(4,8\right)[/latex]. Write the final equation in slope-intercept form.
Solution
Using the point-slope formula, substitute [latex]-3[/latex] for m and the point [latex]\left(4,8\right)[/latex] for [latex]\left({x}_{1},{y}_{1}\right)[/latex].
Analysis of the Solution
Note that any point on the line can be used to find the equation. If done correctly, the same final equation will be obtained.
Try It 8
Given [latex]m=4[/latex], find the equation of the line in slope-intercept form passing through the point [latex]\left(2,5\right)[/latex].
Example 10: Finding the Equation of a Line Passing Through Two Given Points
Find the equation of the line passing through the points [latex]\left(3,4\right)[/latex] and [latex]\left(0,-3\right)[/latex]. Write the final equation in slope-intercept form.
Solution
First, we calculate the slope using the slope formula and two points.
Next, we use the point-slope formula with the slope of [latex]\frac{7}{3}[/latex], and either point. Let’s pick the point [latex]\left(3,4\right)[/latex] for [latex]\left({x}_{1},{y}_{1}\right)[/latex].
In slope-intercept form, the equation is written as [latex]y=\frac{7}{3}x - 3[/latex].
Analysis of the Solution
To prove that either point can be used, let us use the second point [latex]\left(0,-3\right)[/latex] and see if we get the same equation.
We see that the same line will be obtained using either point. This makes sense because we used both points to calculate the slope.
Standard Form of a Line
Another way that we can represent the equation of a line is in standard form. Standard form is given as
where [latex]A[/latex], [latex]B[/latex], and [latex]C[/latex] are integers. The x- and y-terms are on one side of the equal sign and the constant term is on the other side.
Example 11: Finding the Equation of a Line and Writing It in Standard Form
Find the equation of the line with [latex]m=-6[/latex] and passing through the point [latex]\left(\frac{1}{4},-2\right)[/latex]. Write the equation in standard form.
Solution
We begin using the point-slope formula.
From here, we multiply through by 2, as no fractions are permitted in standard form, and then move both variables to the left aside of the equal sign and move the constants to the right.
This equation is now written in standard form.
Try It 9
Find the equation of the line in standard form with slope [latex]m=-\frac{1}{3}[/latex] and passing through the point [latex]\left(1,\frac{1}{3}\right)[/latex].
Vertical and Horizontal Lines
The equations of vertical and horizontal lines do not require any of the preceding formulas, although we can use the formulas to prove that the equations are correct. The equation of a vertical line is given as
where c is a constant. The slope of a vertical line is undefined, and regardless of the y-value of any point on the line, the x-coordinate of the point will be c.
Suppose that we want to find the equation of a line containing the following points: [latex]\left(-3,-5\right),\left(-3,1\right),\left(-3,3\right)[/latex], and [latex]\left(-3,5\right)[/latex]. First, we will find the slope.
Zero in the denominator means that the slope is undefined and, therefore, we cannot use the point-slope formula. However, we can plot the points. Notice that all of the x-coordinates are the same and we find a vertical line through [latex]x=-3[/latex].
The equation of a horizontal line is given as
where c is a constant. The slope of a horizontal line is zero, and for any x-value of a point on the line, the y-coordinate will be c.
Suppose we want to find the equation of a line that contains the following set of points: [latex]\left(-2,-2\right),\left(0,-2\right),\left(3,-2\right)[/latex], and [latex]\left(5,-2\right)[/latex]. We can use the point-slope formula. First, we find the slope using any two points on the line.
Use any point for [latex]\left({x}_{1},{y}_{1}\right)[/latex] in the formula, or use the y-intercept.
The graph is a horizontal line through [latex]y=-2[/latex]. Notice that all of the y-coordinates are the same.
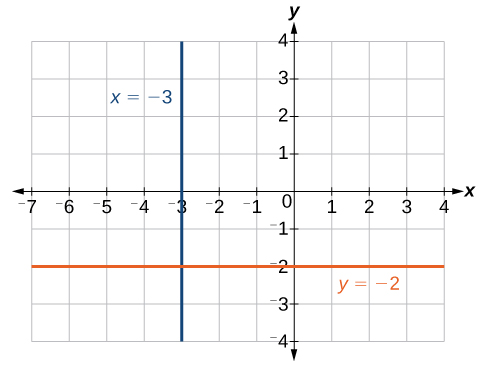
Figure 3. The line x = −3 is a vertical line. The line y = −2 is a horizontal line.
Example 12: Finding the Equation of a Line Passing Through the Given Points
Find the equation of the line passing through the given points: [latex]\left(1,-3\right)[/latex] and [latex]\left(1,4\right)[/latex].
Solution
The x-coordinate of both points is 1. Therefore, we have a vertical line, [latex]x=1[/latex].
Try It 10
Find the equation of the line passing through [latex]\left(-5,2\right)[/latex] and [latex]\left(2,2\right)[/latex].