The intercepts of a graph are points at which the graph crosses the axes. The x-intercept is the point at which the graph crosses the x-axis. At this point, the y-coordinate is zero. The y-intercept is the point at which the graph crosses the y-axis. At this point, the x-coordinate is zero.
To determine the x-intercept, we set y equal to zero and solve for x. Similarly, to determine the y-intercept, we set x equal to zero and solve for y. For example, lets find the intercepts of the equation [latex]y=3x - 1[/latex].
To find the x-intercept, set [latex]y=0[/latex].
To find the y-intercept, set [latex]x=0[/latex].
We can confirm that our results make sense by observing a graph of the equation as in Figure 10. Notice that the graph crosses the axes where we predicted it would.
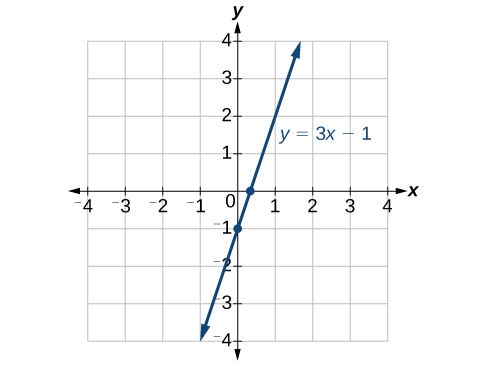
Figure 12
How To: Given an equation, find the intercepts.
- Find the x-intercept by setting [latex]y=0[/latex] and solving for [latex]x[/latex].
- Find the y-intercept by setting [latex]x=0[/latex] and solving for [latex]y[/latex].
Example 4: Finding the Intercepts of the Given Equation
Find the intercepts of the equation [latex]y=-3x - 4[/latex]. Then sketch the graph using only the intercepts.
Solution
Set [latex]y=0[/latex] to find the x-intercept.
Set [latex]x=0[/latex] to find the y-intercept.
Plot both points, and draw a line passing through them as in Figure 11.
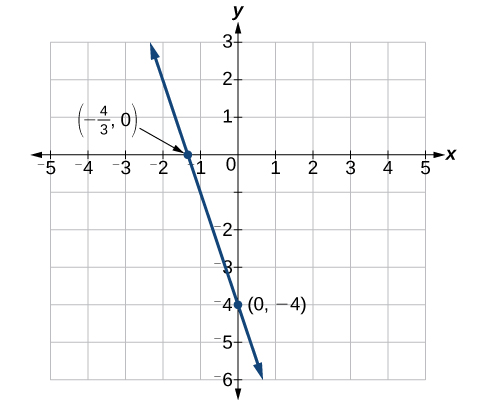
Figure 13
Try It 1
Find the intercepts of the equation and sketch the graph: [latex]y=-\frac{3}{4}x+3[/latex].
Candela Citations
- College Algebra. Authored by: OpenStax College Algebra. Provided by: OpenStax. Located at: http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@3.278:1/Preface. License: CC BY: Attribution