Another transformation that can be applied to a function is a reflection over the x– or y-axis. A vertical reflection reflects a graph vertically across the x-axis, while a horizontal reflection reflects a graph horizontally across the y-axis. The reflections are shown in Figure 9.
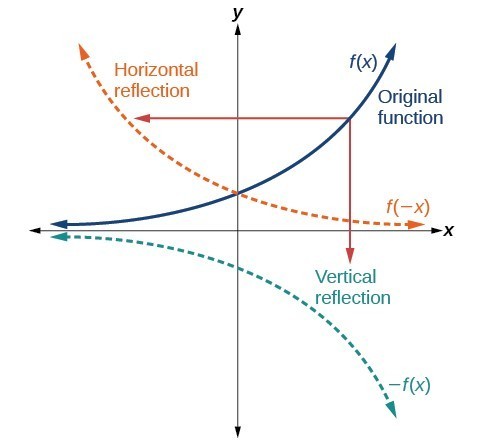
Figure 9. Vertical and horizontal reflections of a function.
Notice that the vertical reflection produces a new graph that is a mirror image of the base or original graph about the x-axis. The horizontal reflection produces a new graph that is a mirror image of the base or original graph about the y-axis.
A General Note: Reflections
Given a function [latex]f\left(x\right)[/latex], a new function [latex]g\left(x\right)=-f\left(x\right)[/latex] is a vertical reflection of the function [latex]f\left(x\right)[/latex], sometimes called a reflection about (or over, or through) the x-axis.
Given a function [latex]f\left(x\right)[/latex], a new function [latex]g\left(x\right)=f\left(-x\right)[/latex] is a horizontal reflection of the function [latex]f\left(x\right)[/latex], sometimes called a reflection about the y-axis.
How To: Given a function, reflect the graph both vertically and horizontally.
- Multiply all outputs by –1 for a vertical reflection. The new graph is a reflection of the original graph about the x-axis.
- Multiply all inputs by –1 for a horizontal reflection. The new graph is a reflection of the original graph about the y-axis.
Example 7: Reflecting a Graph Horizontally and Vertically
Reflect the graph of [latex]s\left(t\right)=\sqrt{t}[/latex] (a) vertically and (b) horizontally.
Solution
a. Reflecting the graph vertically means that each output value will be reflected over the horizontal t-axis as shown in Figure 10.
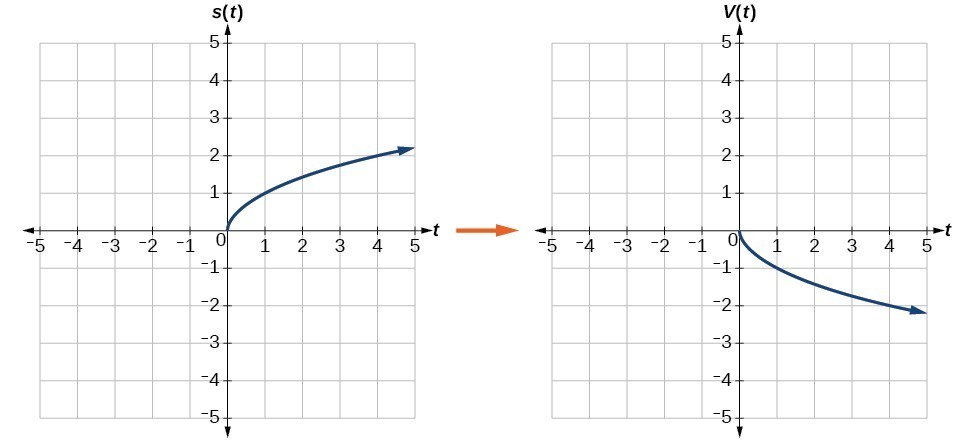
Figure 10. Vertical reflection of the square root function
Because each output value is the opposite of the original output value, we can write
Notice that this is an outside change, or vertical shift, that affects the output [latex]s\left(t\right)[/latex] values, so the negative sign belongs outside of the function.
b.
Reflecting horizontally means that each input value will be reflected over the vertical axis as shown in Figure 11.
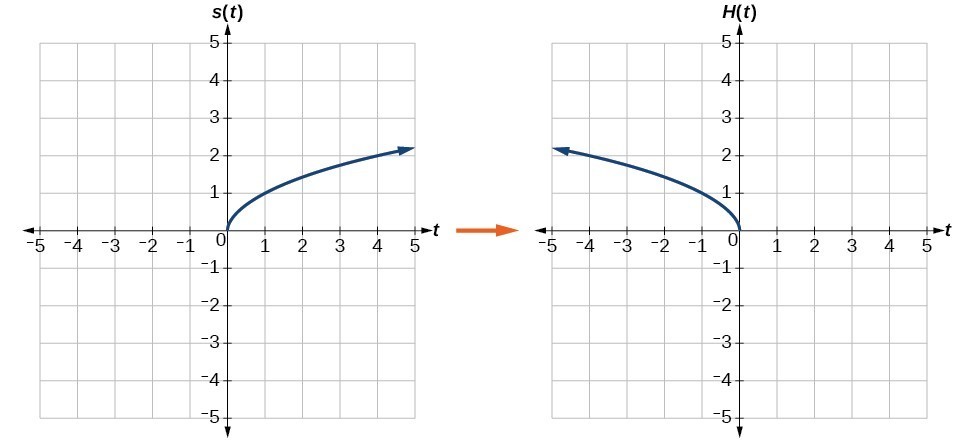
Figure 11. Horizontal reflection of the square root function
Because each input value is the opposite of the original input value, we can write
Notice that this is an inside change or horizontal change that affects the input values, so the negative sign is on the inside of the function.
Note that these transformations can affect the domain and range of the functions. While the original square root function has domain [latex]\left[0,\infty \right)[/latex] and range [latex]\left[0,\infty \right)[/latex], the vertical reflection gives the [latex]V\left(t\right)[/latex] function the range [latex]\left(-\infty ,0\right][/latex] and the horizontal reflection gives the [latex]H\left(t\right)[/latex] function the domain [latex]\left(-\infty ,0\right][/latex].
Try It 2
Reflect the graph of [latex]f\left(x\right)=|x - 1|[/latex] (a) vertically and (b) horizontally.
Example 8: Reflecting a Tabular Function Horizontally and Vertically
A function [latex]f\left(x\right)[/latex] is given. Create a table for the functions below.
- [latex]g\left(x\right)=-f\left(x\right)[/latex]
- [latex]h\left(x\right)=f\left(-x\right)[/latex]
| [latex]x[/latex] | 2 | 4 | 6 | 8 |
| [latex]f\left(x\right)[/latex] | 1 | 3 | 7 | 11 |
Solution
-
For [latex]g\left(x\right)[/latex], the negative sign outside the function indicates a vertical reflection, so the x-values stay the same and each output value will be the opposite of the original output value.
[latex]x[/latex] 2 4 6 8 [latex]g\left(x\right)[/latex] –1 –3 –7 –11 -
For [latex]h\left(x\right)[/latex], the negative sign inside the function indicates a horizontal reflection, so each input value will be the opposite of the original input value and the [latex]h\left(x\right)[/latex] values stay the same as the [latex]f\left(x\right)[/latex] values.
[latex]x[/latex] −2 −4 −6 −8 [latex]h\left(x\right)[/latex] 1 3 7 11
Try It 3
| [latex]x[/latex] | −2 | 0 | 2 | 4 |
| [latex]f\left(x\right)[/latex] | 5 | 10 | 15 | 20 |
Using the function [latex]f\left(x\right)[/latex] given in the table above, create a table for the functions below.
a. [latex]g\left(x\right)=-f\left(x\right)[/latex]
b. [latex]h\left(x\right)=f\left(-x\right)[/latex]
Candela Citations
- Precalculus. Authored by: Jay Abramson, et al.. Provided by: OpenStax. Located at: http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@5.175. License: CC BY: Attribution. License Terms: Download For Free at : http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@5.175.